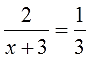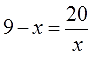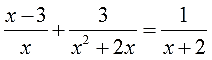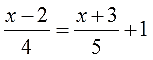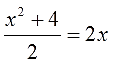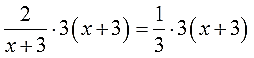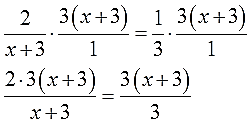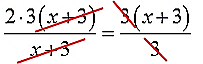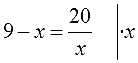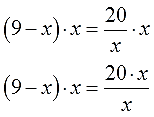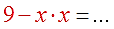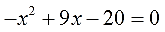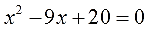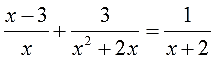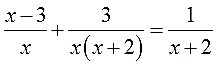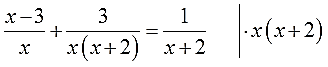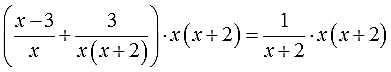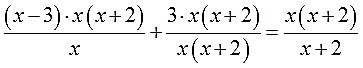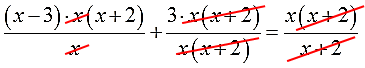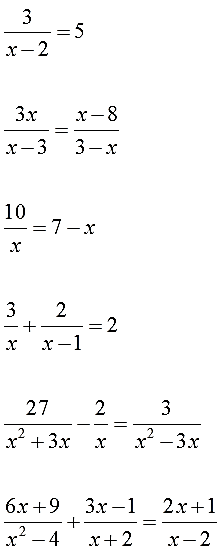Что бы избавится от дроби

Калькулятор дробей

Как перевести смешанную дробь в обыкновенную

Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i n d = i · d + n d

5 3 4 = 5 · 4 + 3 4 = 23 4

Как перевести обыкновенную дробь в смешанную

Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:

1. Поделить числитель дроби на её знаменатель
2. Результат от деления будет являться целой частью
3. Остаток отделения будет являться числителем

Как перевести обыкновенную дробь в десятичную

Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.

Как перевести десятичную дробь в обыкновенную или смешанную

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:

1. Записать дробь в виде десятичная дробь 1
2. Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
3. Найти наибольший общий делитель и сократить дробь.

Например, переведем 0.36 в обыкновенную дробь:

1. Записываем дробь в виде: 0.36 1
2. Умножаем на 10 два раза, получим 36 100
3. Сокращаем дробь 36 100 = 9 25

Как перевести дробь в проценты

Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.

Как перевести проценты в дробь

Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.

Сложение дробей

Алгоритм действий при сложении двух дробей такой:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Выполнить сложение дробей путем сложения их числителей.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Вычитание дробей

Алгоритм действий при вычитании двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Умножение дробей

Алгоритм действий при умножении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
3. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
4. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Деление дробей

Алгоритм действий при делении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
3. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Источник

Вычитание дробей

О чем эта статья:

4 класс, 5 класс, 6 класс

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем. А под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дробей

1. Дробь не имеет значения, при условии, если делитель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Равными называют a/b и c/d в том случае, если a * d = b * c.

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Правило вычитания дробей

Вычитание — арифметическое действие, когда от одного числа отнимают другое.

Свойства вычитания:

1. Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое, а после из результата вычесть другое слагаемое:
   a — (b + c) = (a — b) — c,
   a — (b + c) = (a — с) — b.

1. Скобки в выражении (a — b) — c не имеют значения и их можно опустить:
   (a — b) — c = a — b — c.

1. Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся:
   (a + b) — c = (a — c) + b, если a > c или а = с,
   (a + b) — c = (b — c) + a, если b > c или b = с.

1. Если из числа вычесть нуль, получится оно же:
   a — 0 = a.

1. Если из числа вычесть его само, получится нуль:
   a — a = 0.

Записывайтесь на наши дополнительные занятия по математике, для учеников с 1 по 11 классы!

Вычитание дробей с одинаковыми знаменателями

Для вычитания дробей с одинаковыми знаменателями нужно от числителя первой отнять числитель второй, а знаменатель оставить тот же.

Прежде, чем зафиксировать ответ, важно проверить возможность сокращения.

Рассмотрим это правило на примере:

Вычитание дробей с разными знаменателями

Как вычитать дроби с разными знаменателями? Для этого приводим их к общему знаменателю и гаходим разность числителей.

Рассмотрим пример, в котором нужно найти разность 2/9 и 1/15.

Как решаем:

• Знаменатели разные, значит найдем наименьшее общее кратное (далее — НОК) для определения единого делителя. Для этого записываем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (9, 15) = 3 * 3 * 5 = 45

• Найдем дополнительные множители. Для этого НОК делим на каждый знаменатель:

• Полученные числа умножим на соответствующие дроби:

• Перейдем к вычитанию заданных чисел:

Вычитание обыкновенной дроби из натурального числа

Для вычитания из обыкновенной дроби натурального числа необходимо это действие привести к вычитанию обыкновенных дробей.

Разберем для наглядности пример разности 3 и 6/7.

Как решаем:

• Представим натуральное число в виде смешанного — займем единицу и переведем ее в неправильную дробь с тем же знаменателем, что у вычитаемой:

Ответ: две целых одна седьмая.

Вычитание натурального числа из обыкновенной дроби

Для вычитания натурального числа из обыкновенной дроби нужно последовать тому же алгоритму, что и в предыдущем примере. А именно: перевести натуральное число в вид дроби, привести все к единому знаменателю, найти разность.

Рассмотрим пример разности 3 из 83/21.

Как решаем:

А еще можно вот так:

• Представим 83/21 в виде смешанной дроби, для этого разделим делитель на делимое:

3 * 20/21 — 3 = 20/21

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Как решать дробные уравнения?

Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.

Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)

Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:

1. Дроби и действия с дробями и дробными выражениями.

3. Решение линейных и квадратных уравнений.

Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т.д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)

Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.

Что такое дробное уравнение? Примеры.

Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.

Например, вот такое уравнение:

И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.

Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.

Или такое уравнение:

Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.

В общем, вы поняли.

Как решать дробные уравнения? Убираем дроби!

Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?

Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)

Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?

Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)

Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:

Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.

А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?

Давайте его конструировать.) Смотрим ещё раз на уравнение:

Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)

Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.

Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).

Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:

Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!

А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:

Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:

А его (надеюсь) уже решит каждый:

Решаем следующий примерчик:

И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.

Вот и домножаем! Всю левую часть и всю правую часть:

Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».

А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!

Дело всё в том, что частенько после умножения народ записывает левую часть вот так:

Это категорически неверно. Дальше можно уже не решать, да…)

Но у нас всё хорошо, будем дорешивать.

С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.

Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:

Переносим всё влево и приводим к стандартному виду:

Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:

Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:

Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.

А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.

Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…

Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)

Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.

Раскладываем на множители!

Решаем третье уравнение по списку:

А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить

и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?

Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)

А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х 2 +2х вполне себе раскладывается! Выносим один икс за скобку и получаем:

Отлично. Вставим наше разложение в исходное уравнение:

Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).

Вот на х(х+2) и умножаем:

И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:

А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:

Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)

С удовольствием сокращаем все дроби:

Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:

И снова получили квадратное уравнение.) Решаем и получаем два корня:

Вот и всё. Это и есть ответ.)

Из этого примера можно сделать важный вывод:

Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!

Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)

Ну что, порешаем?)

Ответы (как обычно, вразброс):

Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)

Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!

Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…

Источник