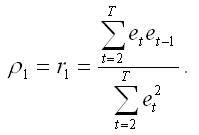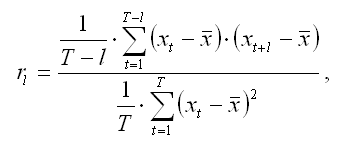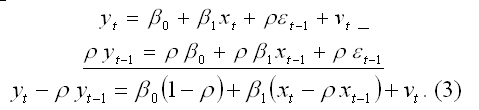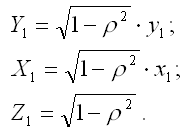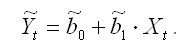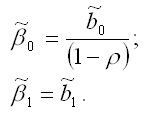Как избавиться от автокорреляции остатков

Устранение автокорреляции остатков модели регрессии

В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков должна быть устранена.

Устранить автокорреляцию остатков модели регрессии можно с помощью включения в модель автокорреляционного параметра, однако на практике данный подход реализовать весьма затруднительно, потому что оценка коэффициента автокорреляции является величиной заранее неизвестной.

Авторегрессионной схемой первого порядка называется метод устранения автокорреляции первого порядка между соседними членами остаточного ряда в линейных моделях регрессии либо моделях регрессии, которые можно привести к линейному виду.

На практике применение авторегрессионной схемы первого порядка требует априорного знания величины коэффициента автокорреляции. Однако в связи с тем, что величина данного коэффициента заранее неизвестна, в качестве его оценки рассчитывается выборочный коэффициент остатков первого порядка ρ₁.

Выборочный коэффициент остатков первого порядка ρ₁ рассчитывается по формуле:

В общем случае коэффициент автокорреляции порядка l рассчитывается по формуле:

где l – временной лаг;

T – число наблюдений;

t – момент времени, в который осуществлялось наблюдение;

x – среднее значение исходного временного ряда.

Предположим, что на основе собранных наблюдений была построена линейная парная модель регрессии:

Рассмотрим применение авторегрессионной схемы первого порядка на примере данной модели.

Исходная линейная модель парной регрессии с учётом процесса автокорреляции остатков первого порядка в момент времени t может быть представлена в виде:

где ρ – коэффициент автокорреляции, |ρ| 2 (ν_t).

Модель регрессии в момент времени (t-1) может быть представлена виде:

Если модель регрессии в момент времени (t-1) умножить на величину коэффициента автокорреляции β и вычесть её из исходной модели регрессии в момент времени t, то в результате мы получим преобразованную модель регрессии, учитывающую процесс автокорреляции первого порядка:

Для более наглядного представления преобразованной модели воспользуемся методом замен:

В результате преобразованная модель регрессии примет вид:

В преобразованной модели регрессии случайная ошибка β_t не подвержена процессу автокорреляции, поэтому можно считать автокорреляционную зависимость остатков модели устранённой.

Авторегрессионную схему первого порядка можно применить ко всем строкам матрицы данных Х, кроме первого наблюдения. Однако если не вычислять Y1 и X1, то подобная потеря в небольшой выборке может привести к неэффективности оценок коэффициентов преобразованной модели регрессии. Данная проблема решается с помощью поправки Прайса-Уинстена. Введём следующие обозначения:

Тогда оценки неизвестных коэффициентов преобразованной модели регрессии (4) можно рассчитать с помощью классического метода наименьших квадратов:

Оценки коэффициентов исходной модели регрессии (1) определяются по формулам:

В результате оцененная модель регрессии будет иметь вид:

Источник

§ 4. Методы устранения автокорреляции

Основной причиной наличия случайного члена в модели являются несовершенные знания о причинах и взаимосвязях, определяющих то или иное значение зависимой переменной. Поэтому свойства случайных отклонений, в том числе и автокорреляция, в первую очередь зависят от выбора формулы зависимости и состава объясняющих переменных.

Однако если все разумные процедуры изменения спецификации модели исчерпаны, а автокорреляция имеет место, то можно предположить, что она обусловлена какими-то внутренними свойствами ряда . В этом случае можно воспользоваться авторегрессионным преобразованием. В линейной регрессионной модели либо в моделях, сводящихся к линейной, наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка AR(1).

Для простоты изложения AR(1) рассмотрим модель парной линейной регрессии:

Тогда наблюдениям t и (t — 1) соответствуют формулы:

Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка:

гд — случайные отклонения, удовлетворяющие

всем предпосылкам МНК, а коэффициент р известен.

Так как по предположению коэффициент р известен, то оче-

видно, у*, xt, vt вычисляются достаточно просто. В силу того что случайные отклонения vt удовлетворяют предпосылкам МНК, оценки параметров в 0 и в1 будут обладать свойствами наилучших линейных несмещенных оценок.

Способ вычисления уt, xt приводит к потере первого наблюдения (если мы не обладаем предшествующим ему наблюдением). Число степеней свободы уменьшится на единицу, что при больших выборках не так существенно, но при малых может привести к потере эффективности. Эта проблема обычно преодолевается с помощью поправки Прайса-Винстена:

Отметим, что авторегрессионное преобразование может быть обобщено на произвольное число объясняющих переменных, т. е. использовано для уравнения множественной регрессии.

Авторегрессионное преобразование первого порядка AR(1) может быть обобщено на преобразования более высоких порядков AR(2), AR(3) и т. д.:

Можно показать, что в случае автокорреляции остатков ковариационная матрица вектора случайных отклонений имеет вид:

В обобщенном методе наименьших квадратов, если известны элементы матрицы Q, параметры уравнения регрессии определяются по формуле Эйткена (AC AifkenV

Однако на практике значение коэффициента р обычно неизвестно и его необходимо оценивать.

Рассмотрим определение р на основе статистики Дарбина- Уотсона.

Напомним, что статистика Дарбина-Уотсона тесно связана с коэффициентом корреляции между соседними отклонениями через соотношение:

Тогда в качестве оценки коэффициента р может быть взят коэффициент r = r :

Этот метод оценивания весьма неплох при большом числе наблюдений. В этом случае оценка r параметра р будет достаточно точной.

Другим возможным методом оценивания р и устранения автокорреляции остатков является итеративный процесс, называемый методом Кохрана-Оркатта. Опишем данный метод на примере парной регрессии:

и авторегрессионной схемы первого порядка St = р St-1 + Vt.

Оцениваетсяпо мнк регрессия Y = в0 + в1 X + s (находится

и определяются остатки (оценки

Пусть р — оценка коэффициента р .

На основе данной оценки строится уравнение:

Коэффициенты в0, в1 оцениваются по уравнению регрессии:

Значения b0 = b0/(1 — /Р),b1 подставляются в Y = b0 + bX . Вновь вычисляются оценки et = yt-yt, t = 1, 2. T отклонений et

и процесс возвращается к этапу 2.

Чередование этапов осуществляется до тех пор, пока не будет достигнута требуемая точность, т. е. пока разность между предыдущей и последующей оценками р не станет меньше любого наперед заданного числа.

Вернемся к примеру 4.1. Полагая, что остаток et линейно зависит от предыдущего значения остатка et-1, и оценивая коэффициент р, получим:

Расчетная таблица

При такой оценке р рассчитаем по приведенным выше форму* *

лам значения xt,yt.

Расчетная таблица

Оценим параметры уравнения обычным ме

тодом наименьших квадратов. Получим:

тогда исправленные оценки коэффициентов исходного уравнения

(первоначальные оценки равны b0 = 2,09, b1 = 2,014). Мы выполнили один цикл процедуры Кохрана-Оркатта.

По данному методу регрессия (4.10) оценивается для каждого возможного значения р из отрезка [-1, 1] с небольшим шагом (например, 0,001; 0,01 и т. д.). Величина р, дающая наименьшую стандартную ошибку регрессии, принимается в качестве оценки коэффициента р . И значения в0, в1 оцениваются из уравнения

регрессии yt = b 0 + b1xt именно с данным значением р . Этот метод широко используется в пакетах прикладных программ.

Итак, подведем итог. В силу ряда причин (ошибок спецификации, инерционности рассматриваемых зависимостей и др.) в регрессионных моделях может иметь место корреляционная зависимость между соседними случайными отклонениями. Это нарушает одну из фундаментальных предпосылок МНК. Вследствие этого оценки, полученные на основе МНК, перестают быть эффективными. Это делает ненадежными выводы по значимости коэффициентов регрессии и по качеству самого уравнения. Поэтому достаточно важным является умение определить наличие автокорреляции и устранить это нежелательное явление. При установлении автокорреляции необходимо в первую очередь проанализировать правильность спецификации модели. Если после ряда возможных усовершенствований регрессии (уточнения состава объясняющих переменных либо изменения формы зависимости) автокорреляция по-прежнему имеет место, то, возможно, это связано с внутренними свойствами ряда отклонений . В этом случае возможны определенные преобразования, устраняющие автокорреляцию. Среди них выделяется авторегрессионная схема первого порядка AR(1), которая, в принципе, может быть обобщена в AR(k), k = 2, 3, . Для применения указанных схем необходимо оценить коэффициент корреляции между отклонениями. Это может быть сделано различными методами: на основе статистики Дарбина-Уотсона, Кохрана-Оркатта, Хилдрета-Лу и др. В случае наличия среди объясняющих переменных лаговой зависимой переменной наличие автокорреляции устанавливается с помощью й-статистики Дарби- на. А для ее устранения в этом случае предпочтителен метод Хилдрета-Лу.

Рассмотрим применение формулы Эйткена для авторегрессионной схемы первого порядка. В этом случае:

Подставив в матрицу Q 1 вместо параметра р его оценку, найдем оценку коэффициентов уравнения по формуле Эйткена:

При автокорреляции случайных возмущений оценки параметров регрессионной модели остаются несмещенными и состоятельными, но становятся неэффективными, и их стандартные ошибки оцениваются неправильно, часто занижаются. Критерий Дарбина-Уотсона является одним из методов обнаружения автокорреляции остатков регрессионной модели. Этот критерий применяется только для обнаружения автокорреляции первого порядка между соседними рядами случайных остатков. Наиболее простым и распространенным методом обнаружения автокорреляции случайных остатков регрессионной модели является графический метод, сутью которого является построение графиков автокорреляционной и частной автокорреляционной функций. Для устранения автокорреляции можно применять методы Кохрана-Оркатта и Хилдрета-Лу.

Вопросы для самопроверки

Как ведут себя остатки относительно линии регрессии в случае положительной автокорреляции случайных возмущений?
Как ведут себя остатки относительно линии регрессии в случае отрицательной автокорреляции случайных возмущений?
Как выглядит ковариационная матрица вектора случайных отклонений, если предпосылки Гаусса-Маркова выполняются?
Как выглядит ковариационная матрица вектора случайных отклонений в случае автокорреляции?
Как выглядит ковариационная матрица вектора случайных отклонений в случае автокорреляции этих отклонений в соседних наблюдениях?
Сохраняется ли несмещенность оценок параметров линейной модели при автокорреляции случайных возмущений?
Сохраняется ли эффективность оценок параметров линейной модели при автокорреляции случайных возмущений?
Сохраняется ли состоятельность оценок параметров линейной модели при автокорреляции случайных возмущений?
По какой формуле рассчитывается статистика Дарбина- Уотсона?
Сколько критических значений имеет статистика Дарбина- Уотсона?
В каких диапазонах статистики Дарбина-Уотсона имеется автокорреляция случайных возмущений?
Запишите формулы, по которым преобразуются переменные в методе Кохрана-Оркатта.
Когда применяется обобщенный метод наименьших квадратов?

Источник