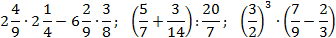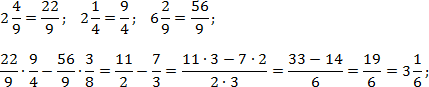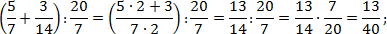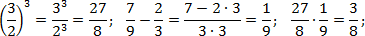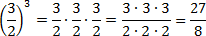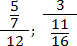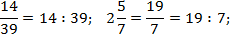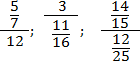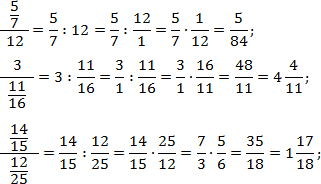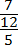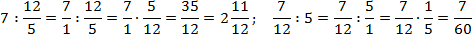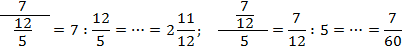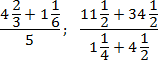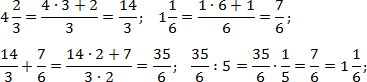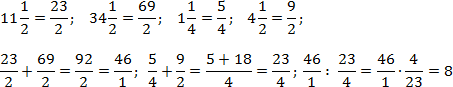Как избавиться от дроби под дробью

Сложные выражения с дробями. Порядок действий

Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?

В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:

1. Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
2. Затем — деление и умножение;
3. Последним шагом выполняется сложение и вычитание.

Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.

Задача. Найдите значения выражений:

Переведем все дроби из первого выражения в неправильные, а затем выполним действия:

Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, . Тогда:

Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, , имеем:

Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.

Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:

Многоэтажные дроби

До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.

Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:

Здесь и далее мы будем называть эти дроби . Однако имейте в виду, что общепризнанного названия у них нет, и в разных учебниках могут встречаться другие определения.

Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:

Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:

Задача. Переведите многоэтажные дроби в обычные:

В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Получаем:

В последнем примере перед окончательным умножением дроби были сокращены.

Специфика работы с многоэтажными дробями

В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:

Это выражение можно прочитать по-разному:

1. В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
2. В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.

Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:

Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.

Если следовать этому правилу, то приведенные выше дроби надо записать так:

Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:

Задача. Найдите значения выражений:

Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:

Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:

Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили в форме дроби, чтобы выполнить деление.

Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.

Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.

Источник

Как вынести из-под корня

Вынесение множителя из-под знака корня — это извлечение корня из одного из множителей (числа или буквы), которые находятся под корнем.

Говорят: «Число « 25 » вынесли из-под знака корня».

Рассмотрим подробнее пример вынесения множителя из-под знака корня.

№ 15 .1 (в) Мордкович 8 класс

Вынесите множитель из-под знака корня:

Извлечь квадратный корень из « √ 5 » целым числом не получится, поэтому нам остается только извлечь квадратный корень из « √ 16 ».

Обязательно выучите таблицу квадратов чисел от « 1 » до « 15 » и таблицу часто используемых квадратных корней.

Вспомним, чему равен квадрат числа четыре?

Решение примера выше записываем следующим образом.

√ 16 · 5 = √ 16 · √ 5 = 4 · √ 5

Действие выше называют вынесением множителя из-под знака корня. Говорят: «Число « 16 » вынесли из-под знака корня, получив число « 4 ».

Выносить из-под знака корня можно, только если все действия под знаком корня — умножение .

Примеры правильного и неправильного вынесения из-под знака корня:

• √ 144 · 2 = √ 144 · √ 2 = 12 √ 2 (верно) . Под знаком квадратного корня только действие умножения;
• √ 16 + 5 ≠ 4 + √ 5 (неверно) . Нельзя выносить « 16 » из-под знака корня, так как под знаком корня сложение ;
• √ 25 − 3 ≠ 5 − √ 3 (неверно) . Нельзя выносить из-под знака корня « 25 », так как под знаком корня вычитание ;
• √ 16 ·2 + 3 ≠ 4 √ 2 + 3 (неверно) . Нельзя выносить « 16 » из-под знака корня, так как под знаком корня есть сложение (должно быть только умножение ).

Как вынести множитель из корня с одним числом

Рассмотрим пример, когда под корнем только одно число и по условию задания требуется вынести множитель из-под знака корня.

№ 524 (1) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

Извлечь целое число из квадратного корня « √ 8 » нельзя, так как нет такого целого числа, которое в квадрате давало бы « 8 ».

Обязательно выучите таблицу квадратов чисел от « 1 » до « 15 » и таблицу часто используемых квадратных корней.

Подумаем, на какие множители можно разложить число « 8 », чтобы была возможность вынести один из множителей из-под знака корня. Вспоминаем таблицу умножения.

Число « 8 » — это произведение
« 8 = 4 · 2 ». Теперь можем вынести « 4 » из-под знака корня.

√ 8 = √ 4 · 2 = √ 4 · √ 2 = 2 √ 2

Разберем другие примеры вынесения множителя из-под знака квадратного корня

№ 524 (4) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

Зададим себе вопрос: «На какие множители нужно разложить « 54 », чтобы была возможность вынести один из множителей из-под знака квадратного корня?».

Видим число « 9 ». Подходит, так как « √ 9 = 3 ».

Завершим решение примера вынесением из-под знака корня числа « 9 ».

√ 54 = √ 9 · 6 = 3 √ 6

Извлечь « √ 6 » целым числом невозможно. Поэтому ответ оставляем в таком виде.

№ 524 (5) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

В примерах с числами, которые делятся на « 10, 100, 1000… » и так далее, стоит сразу попробовать разложить число на « 10, 100, 1000… » и второй множитель.

То есть число « 490 » можно разложить на « 490 = 49 · 10 ». Из « 49 » можно извлечь квадратный корень.

Теперь можно вынести « 49 » из-под знака корня.

√ 490 = √ 49 · 10 = 7 √ 10

№ 524 (6) Мерзляк 8 класс

№ 524 (8) Мерзляк 8 класс

√ 108 = √ 54 · 2 = √ 9 · 6 · 2 =

= 3 √ 6 · 2 = 3 √ 12 = 3 √ 4 · 3 =

№ 526 (6) Мерзляк 8 класс

0,4 · √ 250 = 0,4 · √ 25 · 10 =

Завершим пример, умножив десятичную дробь « 0,4 » на « 5 » по правилу умножения десятичной дроби на число.

0,4 · √ 250 = 0,4 · √ 25 · 10 =

= 0,4 · 5 √ 10 = 2 √ 10

№ 526 (8) Мерзляк 8 класс

4

9

· √ 63 =

4

9

· √ 9 · 7 =

4

9

· 3 √ 7 = …
Умножим дробь «

4

9

» на число « 3 », которое вынесли из-под знака квадратного корня. Используем правило умножения обыкновенной дроби на число.

4

9

· √ 63 =

4

9

· √ 9 · 7 =

4

9

· 3 √ 7 =

=

4 · 3

9

· √ 7 =

4 · 3

9 3

· √ 7 =

=

4

3

· √ 7 = …

Чтобы дать окончательный ответ, выделим целую часть неправильной дроби «

4

3

».

4

9

· √ 63 =

4

9

· √ 9 · 7 =

4

9

· 3 √ 7 =

=

4 · 3

9

· √ 7 =

4 · 3

9 3

· √ 7 =

4

3

· √ 7 =

= 1

1

3

· √ 7

Как вынести десятичную дробь из-под знака корня

В уроке «Как извлечь квадратный корень из дроби» мы разбирали, каким образом извлечь квадратный корень из десятичной дроби. Например, извлечение квадратного корня из десятичной дроби « √ 0,25 ».

√ 0,25 = 0,5 , так как
0,5 2 = 0,5 · 0,5 = 0,25

Тот же самый метод используется при вынесении десятичной дроби из-под знака корня.

№ 524 (10) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

Разложим десятичную дробь на произведение множителей, чтобы потом была возможность вынести один из множителей из-под знака корня.

Подберем десятичную дробь, на которую делится « 0,48 », из которой потом можно извлечь квадратный корень.

Например, « 0,16 ». Десятичная дробь « 0,48 » делится на « 0,16 » нацело.

Извлечь квадратный корень из « √ 0,16 » по правилу нахождения квадратного корня из десятичной дроби.

Завершим пример вынесением « 0,16 » из-под знака корня.

Примеры вынесения десятичной дроби из-под знака квадратного корня

№ 524 (9) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

№ 526 (7) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

−2 · √ 0,18 = −2 · √ 0,09 · 2 =

= −2 · 0,3 √ 2 = −0,6 √ 2

Как вынести букву из-под знака корня

При вынесении из-под знака квадратного корня множителя в степени (буквы или числа) степень делится на « 2 ».

• √ a 2 = a
  

  2

  2

  = a 1 = a , гдe a ≥ 0

• √ y 4 = y
  

  4

  2

  = y 2 , гдe y ≥ 0

• √ 12 4 = 12
  

  4

  2

  = 12 2 = 144

• √ x 6 = x
  

  6

  2

  = x 3 , гдe x ≥ 0

Рассмотрим примеры вынесения буквы в степени из-под корня.

№ 347 (2, 4) Колягин (Алимов) 8 класс

Вынести множитель из-под знака корня (буквами обозначены положительные числа).

2) √ 2x 2 = x

2

2

√ 2 = x √ 2

4) √ 3a 6 = a

6

2

√ 3 = a 3 √ 3

В более сложных примерах требуется вынести и числовой множитель, и букву в степени из-под корня.

№ 348 (2) Колягин (Алимов) 8 класс

Вынести множитель из-под знака корня (буквами обозначены положительные числа).

Вначале отдельно вынесем буквенный множитель из-под корня.

√ 75a 2 = a

2

2

· √ 75 = a √ 75 = …

Теперь разложим число « 75 » на множители, один из которых можно вынести из-под знака квадратного корня.

Число « 75 » явно делится на « 5 ». Проверим, можно ли число « 75 » разложить на квадрат числа « 5 2 = 25 ».

Завершим пример, вынеся число « 25 » из-под знака корня.

√ 75a 2 = a

2

2

· √ 75 = a √ 75 =

= a √ 25 · 3 = 5a √ 3

№ 549 (2) Мерзляк 8 класс

Не всегда удается сразу вынести букву в степени из-под знака корня. В данном примере степень « 9 » не делится нацело на « 2 ».

Вспомним из урока «Свойства степени» правило произведение степеней с одинаковым основанием.

Свойство работает и в обратную сторону.

Вернемся к нашему примеру. Разложим « y 9 » на множители со степенями так, чтобы одна из степеней нацело делилась на « 2 ». Представим степень « 9 » как сумму чисел « 9 = 6 + 3 ».

Используем свойство произведения степеней с одинаковым основанием в обратную сторону и разложим « у » на множители.

Источник