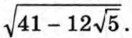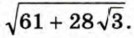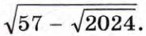Как избавится от двойного радикала

Преобразование двойных радикалов

Сторона а₅ правильного пятиугольника, вписанного в круг радиуса R, вычисляется по формуле

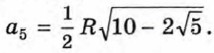
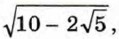
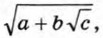
Выражение входящее в эту формулу, имеет вид

где а, b, с — некоторые рациональные числа. Выражение такого вида называют двойным радикалом.

В преобразованиях выражений, содержащих двойные радикалы, стремятся освободиться от внешнего радикала. Это нетрудно сделать, когда выражение, стоящее под знаком радикала, можно представить в виде квадрата суммы или квадрата разности.

Пример 1. Освободимся от внешнего радикала в выражении

Попытаемся представить выражение 41 — 12√5 в виде квадрата разности двух выражений. Для этого 12√5 будем рассматривать как удвоенное произведение двух выражений, а 41 как сумму их квадратов. Выражение 12√5 можно представить, например, как 2 • 6 • √5 или как 2 • 3 • 2√5. Проверка убеждает нас, что именно в первом случае сумма квадратов множителей 6 и √5 равна 41. Значит,

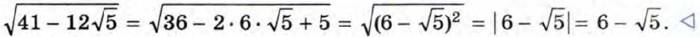
Пример 2. Освободимся от внешнего радикала в выражении

Покажем, как можно решить эту задачу, используя метод неопределённых коэффициентов.

Пусть где а и b — некоторые числа.

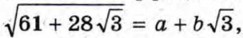
Тогда (а + √3) 2 = 61 + 28√3 и а + b√3 ≥ 0. Значит,

а 2 + 2ab√3 + 3b 2 = 61 + 28√3.

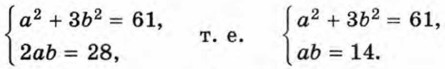
Выпишем все пары целых чисел (а; b), для которых ab = 14: (-14; -1), (-7; -2), (-2; -7), (-1; -14), (1; 14), (2; 7), (7; 2), (14; 1).

Из этих пар выберем те, которые удовлетворяют условиям

а 2 + 3b 2 = 61 и a + b√3 ≥ 0.

Нетрудно убедиться, что такая пара единственная — это пара (7; 2). Значит,

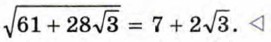
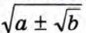
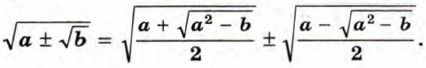
В тех случаях, когда а ≥ 0, b ≥ 0 и разность а2 — b равна квадрату рационального числа, освободиться от внешнего радикала в выражении можно с помощью формулы двойного радикала:

В правой части этой формулы записано неотрицательное число. Покажем, что его квадрат равен а ± √b:

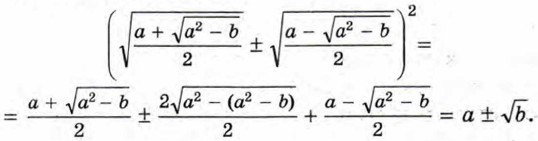
Пример 3. Освободимся от внешнего радикала в выражении

По формуле двойного радикала имеем

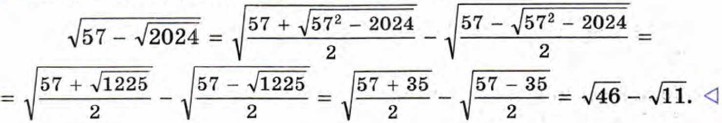
Освобождение от внешнего радикала используется в преобразованиях выражений с переменными, содержащих двойные радикалы.

Пример 4. Упростим выражение

Представим в двойном радикале подкоренное выражение в виде

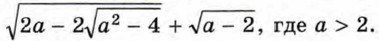
Источник

Сложные радикалы. Освобождение от внешнего корня в сложном радикале

Освобождение от внешнего корня в сложном радикале

Выделение полного квадрата под корнем

Если подкоренное выражение в сложном радикале представляет собой полный квадрат, то можно освободиться от внешнего корня, применив тождество

Освободиться от внешнего радикала в выражении .

Метод неопределенных коэффициентов

Если устный подбор полного квадрата под внешним корнем сложного радикала затруднителен, можно попытаться выделить полный квадрат методом неопределенных коэффициентов

Освободиться от внешнего радикала в выражении

методом неопределенных коэффициентов.

Пусть существуют целые х и у такие, что

Возведем уравнение системы в квадрат:

Тогда

Для целых х и у возможны 4 варианта: (3;1), (1;3), (-3;-1), (-1;-3), второй и третий из которых не удовлетворяют неравенству .

Рассмотрим первый и четвертый варианты:

1.

2. Решений нет.

Следовательно, х = 3, у = 1 и

Применение формул сложных радикалов

В некоторых примерах удается освободиться от внешнего корня с помощью формул сложных радикалов:

В случае если является точным квадратом, эти формулы позволяют представить сложный радикал в виде суммы двух простых радикалов.

Эти формулы можно легко доказать, убедившись в том, что левая и правая части при неотрицательны, и возведя обе части формул в квадрат .

Представьте сложный радикал в виде суммы двух простых радикалов.

Источник

Урок алгебры в 8-м классе на тему: «Преобразование двойных радикалов»

Разделы: Математика

Цели урока:

1) Познакомить учащихся с понятием двойного радикала.

2) Научить преобразовывать двойные радикалы выделением полного квадрата подкоренного выражения и по формулам двойного радикала.

3) Развивать умения и навыки работы с квадратными корнями, выявить закономерности и обобщить учебный материал.

1) Развитие внимания учащихся.

2) Развитие умения слушать товарища, доводить начатое дело до конца.

3) Развитие интереса к изучению алгебры и навыки самостоятельной и исследовательской работы.

1) Воспитание чувства коллективизма.

2) Продолжить формирование чувства ответственности за результат работы.

1 этап работы. Организационный момент.

2 этап работы. Устный счёт.

а) Найти два последовательных натуральных числа, между которыми заключено число:

б) Имеет ли смысл выражение:

в) Упростите выражение:

г) Выполни умножение:

Вводим понятие двойного радикала:

Выражения вида и называют двойными радикалами или сложными радикалами.

Преобразовать двойной радикал – это значит избавиться от внешнего радикала.

Обратим внимание, что во время устного счёта мы с вами уже преобразовывали двойные радикалы. Преобразование двойных радикалов произошло во время алгебраических действий с квадратными корнями.

Преобразовать выражение в тетради:

1)

На этом примере мы убедились, что мы уже умеем преобразовывать двойные радикалы в процессе выполнения алгебраических действий.

2) Вместо “?” поставить числа так, чтобы получилось верное равенство:

Преобразовать следующие выражения, используя формулы полного квадрата:

Вывод: Если подкоренное выражение представить в виде полного квадрата, то можно легко освободиться от внешнего радикала.

Работаем в тетрадях примерам 1;2;3;5 с листа контрольных заданий.

Последний пример пытаются выполнить и не получается.

В тех случаях, когда подкоренное выражение нелегко представить в виде полного квадрата, можно использовать готовые формулы:

При данных условиях каждое подкоренное выражение не отрицательно. Докажем справедливость одной из формул.

Возведём обе части первого равенства в квадрат. Имеем:(доказывает ученик):

Применяя данные формулы решить примеры 7;8;10;17; 21 с листа контрольных заданий.

7)

Вывод урока: преобразовать двойные радикалы можно

1) при выполнении алгебраических действий в некотором выражении, содержащем двойные радикалы.

2) приводя подкоренное выражение к полному квадрату;

3) по формулам сложного радикала.

Дома вы преобразуете двойные радикалы с контрольного листа разными способами.

Источник

Урок по алгебре: «Преобразования двойных радикалов» (8 класс)

Ищем педагогов в команду «Инфоурок»

Преобразования двойных радикалов

1) Познакомить учащихся с понятием двойного радикала.

2) Научить преобразовывать двойные радикалы выделением полного квадрата подкоренного выражения и по формулам двойного радикала.

3) Развивать умения и навыки работы с квадратными корнями, выявить закономерности и обобщить учебный материал.

1) Развитие внимания учащихся.

2) Развитие умения слушать товарища, доводить начатое дело до конца.

3) Развитие интереса к изучению алгебры и навыки самостоятельной и исследовательской работы.

1) Воспитание чувства коллективизма.

2) Продолжить формирование чувства ответственности за результат работы.

1 этап работы. Организационный момент.

2 этап работы. Устный счёт.

а) Найти два последовательных натуральных числа, между которыми заключено число:

б) Имеет ли смысл выражение:

в) Упростите выражение:

г) Выполни умножение:

Вводим понятие двойного радикала:

Выражения вида и называют двойными радикалами или сложными радикалами.

Преобразовать двойной радикал – это значит избавиться от внешнего радикала.

Обратим внимание, что во время устного счёта мы с вами уже преобразовывали двойные радикалы. Преобразование двойных радикалов произошло во время алгебраических действий с квадратными корнями.

Преобразовать выражение в тетради:

1)

На этом примере мы убедились, что мы уже умеем преобразовывать двойные радикалы в процессе выполнения алгебраических действий.

2) Вместо “?” поставить числа так, чтобы получилось верное равенство:

Преобразовать следующие выражения, используя формулы полного квадрата:

Вывод: Если подкоренное выражение представить в виде полного квадрата, то можно легко освободиться от внешнего радикала.

Работаем в тетрадях примерам 1;2;3;5 с листа контрольных заданий.

Последний пример пытаются выполнить и не получается.

В тех случаях, когда подкоренное выражение нелегко представить в виде полного квадрата, можно использовать готовые формулы:

При данных условиях каждое подкоренное выражение не отрицательно. Докажем справедливость одной из формул.

Возведём обе части первого равенства в квадрат. Имеем:(доказывает ученик):

Применяя данные формулы решить примеры 7;8;10;17; 21 с листа контрольных заданий.

7)

Вывод урока: преобразовать двойные радикалы можно

1) при вып-ии алгебраич-х действий в некот выражении, содержащем двойные радикалы.

2) приводя подкоренное выражение к полному квадрату;

3) по формулам сложного радикала.

Дома вы преобразуете двойные радикалы с контрольного листа разными способами.

Источник