- Преобразование двойных радикалов
- Преобразование двойных радикалов
- Алгоритм решения уравнений с двойными радикалами
- Преобразование выражений вида $ \sqrt> $
- Примеры
- Урок по алгебре: «Преобразования двойных радикалов» (8 класс)
- Преобразования двойных радикалов
- Урок алгебры по теме «Двойной радикал». 8-й класс
- Ход урока
- 1 этап работы. Организационный момент.
- 2 этап работы. Мотивация и выход на постановку проблемы
- 3 этап работы. Повторение ранее изученного материала
- 4 этап работы. Ввести понятие двойного радикала и доказатьформулу сложного радикала.
- 5 этап работы. Рассмотрим способы преобразования двойного радикала.
- 6 этап работы. Закрепление изученного материала.
- 7 этап работы. Вывод урока.
- 8 этап работы. Домашнее задание.
Преобразование двойных радикалов
Сторона а5 правильного пятиугольника, вписанного в круг радиуса R, вычисляется по формуле
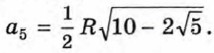
Выражение 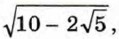
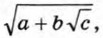
где а, b, с — некоторые рациональные числа. Выражение такого вида называют двойным радикалом.
В преобразованиях выражений, содержащих двойные радикалы, стремятся освободиться от внешнего радикала. Это нетрудно сделать, когда выражение, стоящее под знаком радикала, можно представить в виде квадрата суммы или квадрата разности.
Пример 1. Освободимся от внешнего радикала в выражении

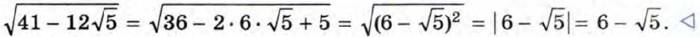
Пример 2. Освободимся от внешнего радикала в выражении
Покажем, как можно решить эту задачу, используя метод неопределённых коэффициентов.

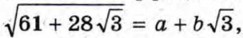
Тогда (а + √3) 2 = 61 + 28√3 и а + b√3 ≥ 0. Значит,
а 2 + 2ab√3 + 3b 2 = 61 + 28√3.
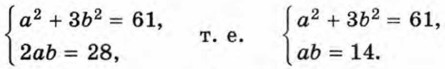
Выпишем все пары целых чисел (а; b), для которых ab = 14: (-14; -1), (-7; -2), (-2; -7), (-1; -14), (1; 14), (2; 7), (7; 2), (14; 1).
Из этих пар выберем те, которые удовлетворяют условиям
а 2 + 3b 2 = 61 и a + b√3 ≥ 0.
Нетрудно убедиться, что такая пара единственная — это пара (7; 2). Значит,
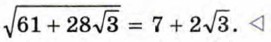
В тех случаях, когда а ≥ 0, b ≥ 0 и разность а2 — b равна квадрату рационального числа, освободиться от внешнего радикала в выражении 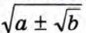
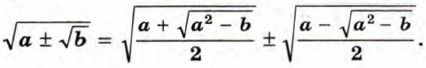
В правой части этой формулы записано неотрицательное число. Покажем, что его квадрат равен а ± √b:
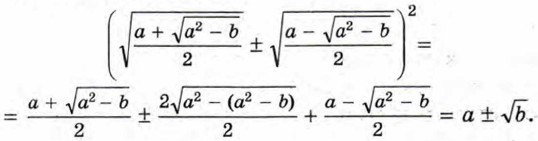
Пример 3. Освободимся от внешнего радикала в выражении

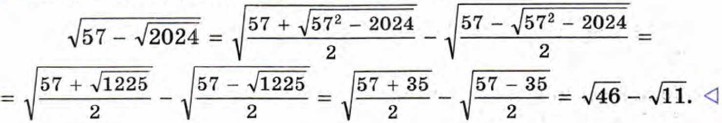
Освобождение от внешнего радикала используется в преобразованиях выражений с переменными, содержащих двойные радикалы.
Пример 4. Упростим выражение
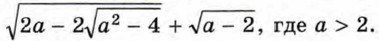

Источник
Преобразование двойных радикалов
Алгоритм решения уравнений с двойными радикалами
Решаем уравнение вида $ \sqrt
Шаг 1. Если $e \ge 0$, возвести в квадрат левую и правую части.
Если $e \lt 0$, решений нет, $x \in \varnothing$, перейти на шаг 5.
Шаг 2. $ax+b \sqrt
Шаг 3. Возвести в квадрат левую и правую части
с условием, что правая часть неотрицательна:
Шаг 4. Решить полученное квадратное уравнение (см. главу 4 данного справочника)
и проверить для корней условие $\frac
Шаг 5. Конец работы.
Преобразование выражений вида $ \sqrt> $
Справедлива следующая формула:
Примеры
Пример 1. Решите уравнения:
Возводим в квадрат: $1+\sqrt<2>+\sqrt
Возводим в квадрат: $2+\sqrt
Возводим в квадрат: x = 49
Возводим в квадрат: $x+2\sqrt
Замечаем, что по определению арифметического корня:
$$ <\left\< \begin
Единственное возможное решение x=1. Подставляем: $ \sqrt<1+2\sqrt<1-1>> ≡ 1$
Пример 2. Вычислите:
Исходное выражение: $A = \pm \sqrt<2>$.
Очевидно, что $\sqrt<9-\sqrt<17>> \lt \sqrt<9 + \sqrt<17>>$ и $A \lt 0$. Поэтому $A = — \sqrt<2>$.
Используем формулу преобразования двойных радикалов.
$$A = 9, B = 17 \Rightarrow C = A^2-B = 81-17 = 64 \Rightarrow \sqrt
$$ A \gt 0: A = \sqrt <4>= 2 $$
Подставляем: $ \frac<4-2> <4>= \frac<1><2>$
Пример 3. Используя формулу преобразования двойных радикалов, упростите выражение:
$$ A = 2, B = 3 \Rightarrow C = A^2-B = 4-3 = 1 \Rightarrow \sqrt
$$ A = 7, B = 24 \Rightarrow C = A^2-B = 49-24 = 25 \Rightarrow \sqrt
$$ A = 11, B = 112 \Rightarrow C = A^2-B = 121-112 = 9 \Rightarrow \sqrt
$$ A = 9, B = 80 \Rightarrow C = A^2-B = 81-80 = 1 \Rightarrow \sqrt
$$ A = a, B = a^2-b^2 \Rightarrow C = A^2-B = a^2-(a^2-b^2 ) = b^2 \Rightarrow \sqrt
Пример 4. Докажите равенство индийского математика Бхаскара (1114-1185):
Возведём в квадрат левую и правую части равенства. Для квадрата суммы трёх выражений используем формулу из §26 справочника для 7 класса.
Выражения слева и справа тождественно равны.
Что и требовалось доказать.
Пример 5*. Упростите выражение (задача Ж.Бертрана (1822-1900)):
Используем результат из примера 3(а):
$$ (\sqrt<3>+1)^2 = 3+2\sqrt<3>+1 = 4+2\sqrt <3>= 2(2+\sqrt<3>) \Rightarrow 2+\sqrt <3>= \frac<(\sqrt<3>+1)^2> <2>$$
Источник
Урок по алгебре: «Преобразования двойных радикалов» (8 класс)
Ищем педагогов в команду «Инфоурок»
Преобразования двойных радикалов
1) Познакомить учащихся с понятием двойного радикала.
2) Научить преобразовывать двойные радикалы выделением полного квадрата подкоренного выражения и по формулам двойного радикала.
3) Развивать умения и навыки работы с квадратными корнями, выявить закономерности и обобщить учебный материал.
1) Развитие внимания учащихся.
2) Развитие умения слушать товарища, доводить начатое дело до конца.
3) Развитие интереса к изучению алгебры и навыки самостоятельной и исследовательской работы.
1) Воспитание чувства коллективизма.
2) Продолжить формирование чувства ответственности за результат работы.
1 этап работы. Организационный момент.
2 этап работы. Устный счёт.
а) Найти два последовательных натуральных числа, между которыми заключено число:
б) Имеет ли смысл выражение:
в) Упростите выражение:
г) Выполни умножение:
Вводим понятие двойного радикала:
Выражения вида 

Преобразовать двойной радикал – это значит избавиться от внешнего радикала.
Обратим внимание, что во время устного счёта мы с вами уже преобразовывали двойные радикалы. Преобразование двойных радикалов произошло во время алгебраических действий с квадратными корнями.
Преобразовать выражение в тетради:
1)
На этом примере мы убедились, что мы уже умеем преобразовывать двойные радикалы в процессе выполнения алгебраических действий.
2) Вместо “?” поставить числа так, чтобы получилось верное равенство:
Преобразовать следующие выражения, используя формулы полного квадрата:
Вывод: Если подкоренное выражение представить в виде полного квадрата, то можно легко освободиться от внешнего радикала.
Работаем в тетрадях примерам 1;2;3;5 с листа контрольных заданий.
Последний пример пытаются выполнить и не получается.
В тех случаях, когда подкоренное выражение нелегко представить в виде полного квадрата, можно использовать готовые формулы:
При данных условиях каждое подкоренное выражение не отрицательно. Докажем справедливость одной из формул.
Возведём обе части первого равенства в квадрат. Имеем:(доказывает ученик):
Применяя данные формулы решить примеры 7;8;10;17; 21 с листа контрольных заданий.
7)
Вывод урока: преобразовать двойные радикалы можно
1) при вып-ии алгебраич-х действий в некот выражении, содержащем двойные радикалы.
2) приводя подкоренное выражение к полному квадрату;
3) по формулам сложного радикала.
Дома вы преобразуете двойные радикалы с контрольного листа разными способами.
Источник
Урок алгебры по теме «Двойной радикал». 8-й класс
Разделы: Математика
Класс: 8
Цели урока:
- Углубить знания учащихся по теме квадратные корни и обобщить учебный материал.
- Познакомить учащихся с понятием двойного радикала.
- Научить преобразовывать двойные радикалы выделением полного квадрата подкоренного выражения.
- Научить учащихся использовать формулу двойного радикала.
- Развивать умения и навыки работы с иррациональными выражениями.
- Развитие внимания учащихся.
- Развитие умения добиваться результатов труда.
- Развитие интереса к изучению алгебры и навыков самостоятельной работы.
- Воспитание чувства коллективизма.
- Формирование чувства ответственности за результат работы.
- Формирование у учащихся адекватной самооценки при выборе отметки за работу на уроке.
Оборудование: компьютер, проектор.
Ход урока
1 этап работы. Организационный момент.
2 этап работы. Мотивация и выход на постановку проблемы
До восьмого класса мы осуществляли над числами пять арифметических действий: сложение, вычитание, умножение, деление и возведение в степень, причем при вычислениях, мы активно использовали различные свойства этих операций.
В курсе алгебры восьмого класса была введена новая операция – извлечение квадратного корня из неотрицательного числа. Выражения, содержащие операцию извлечения квадратного корня, называются иррациональными.
В большом толковом словаре можно найти следующее определение иррациональности:
С философской точки зрения иррациональность – недоступность разуму, то, что не может быть постигнуто разумом, что явно не подчиняется законам логики, и не может быть выражено в логических понятиях, что оценивается как «сверхразумное». С математической точки зрения иррациональность – несоизмеримость с единицей; не является ни целой, ни дробной величиной.
Действительно ли понятие иррациональности – это что-то «уму не постижимое, несоизмеримое, немыслимое»?
На этот вопрос мы постараемся сегодня найти ответ.
3 этап работы. Повторение ранее изученного материала
1) Свойства квадратного корня
Чтобы успешно выполнять преобразования выражений, содержащих операцию извлечения квадратного корня, нужно знать свойства этой операции.
Вспомним эти свойства:
1) Квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней из этих чисел.
2) Если a≥0, b>0, то справедливо равенство
3) Если a≥0 и n – натуральное число, то
4) При любом a справедливо тождество
Если хорошо знать приёмы преобразования рациональных выражений, приёмы преобразования алгебраических дробей, усвоить определение понятия корня и свойства квадратного корня, уметь вносить множитель под знак квадратного корня, выносить множитель из – под знака квадратного корня, то можно выполнить преобразование любого выражения, содержащего операцию извлечения квадратного корня.
2) Способы преобразования радикалов
Кроме перечисленных теорем при преобразовании радикалов применяются некоторые специальные приёмы, тоже вытекающие из этих теорем, но требующие некоторого навыка.
Первый называется уничтожением иррациональности в знаменателе дроби. Если в знаменателе дроби имеется корень или несколько корней, то обращаться с такой дробью не совсем удобно. Смысл этого приёма заключается в том, что надо подобрать такой множитель, чтобы его произведение на знаменатель не содержало корней.
Второе интересное преобразование радикалов называется преобразованием двойного радикала .
4 этап работы. Ввести понятие двойного радикала и доказатьформулу сложного радикала.
Выражения вида 


=
При 
Докажем эти равенства(доказывает ученик):
Для этого возведём в квадрат обе части данных выражений, воспользовавшись при этом формулой квадрата суммы (разности) двух чисел и формулой разности квадратов.
Возведем в квадрат левую часть:
=
Возведем в квадрат правую часть:
=
∙
= =
=
= =
=
=
Заметим, что доказанное тождество позволяет существенно облегчить вычисления и преобразования, если выражение 
5 этап работы. Рассмотрим способы преобразования двойного радикала.
1 способ:
Можно выполнить алгебраические действия в некотором выражении, содержащем двойные радикалы.
Примеры:
=
=
=
= =
=










2 способ
Можно привести подкоренное выражение к полному квадрату.
Примеры:
=
=
= =
=
=
=
=
=
= =
=
=
=
=
= =
Таким образом, если подкоренное выражение представить в виде полного квадрата, то можно легко освободиться от внешнего радикала.
Попробуем решить
НЕ УДАЕТСЯ.
3 способ
В тех случаях, когда подкоренное выражение нелегко представить в виде полного квадрата, то можно использовать готовую формулу сложного радикала
=
Примеры:
=
=
=
=
= =
=
=
=
=
= =
=
=
=
=
= =
=
6 этап работы. Закрепление изученного материала.
Преобразуйте выражения, содержащие двойные радикалы:
7 этап работы. Вывод урока.
Преобразовать двойные радикалы можно следующим образом:
- выполняя в выражении, содержащем двойные радикалы, алгебраические действия, применив свойства квадратных корней;
- приводя подкоренное выражение к полному квадрату;
- используя формулы сложного радикала.
8 этап работы. Домашнее задание.
Дома вы преобразуете двойные радикалы разными способами (раздать листы с заданиями).
Источник

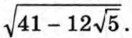
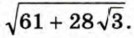
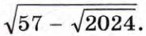

















 =
= 
 =
= 
 =
=  ∙
∙ = =
= =  =
=  = =
= =  =
=  =
= 
 =
=  =
=  =
=  = =
= =  =
= 


 =
= =
= = =
= = =
= =
= =
=
 =
= =
= = =
= = =
=
 =
= =
= =
= = =
= =

 =
= 
 =
= =
= =
= =
= = =
= = =
=
 =
= =
= =
= = =
= = =
=
 =
= =
= =
= = =
= = =
=











