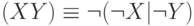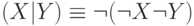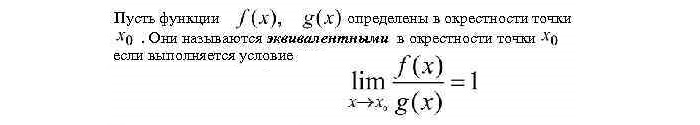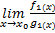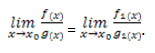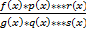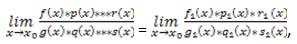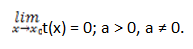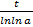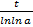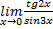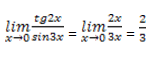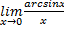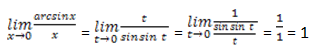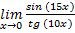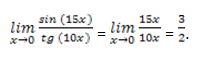Как избавиться от эквивалентности

Эквивалентность формул

Смотреть на youtube || на ИНТУИТ в качестве: низком | среднем | высоком

Одну и ту же функцию можно задать разными формулами. Поэтому возникает задача определения эквивалентности формул логики высказываний.

Две формулы эквивалентны, если они задают одну и ту же функцию. Как можно установить эквивалентность формул? Один из способов состоит в том, чтобы построить таблицу истинности. Если две формулы на всех возможных значениях переменных дают одно и то же значение , то они определяют одну и ту же функцию, следовательно, формулы эквивалентны.

Давайте установим эквивалентности для некоторых функций из таблицы 3 предыдущего урока.

Исключающее Или эквивалентно отрицанию эквивалентности:

Построим таблицы истинности для этих двух формул:

0	0	1	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	0	0

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Штрих Шеффера эквивалентен отрицанию конъюнкции:

Построим таблицы истинности для этих двух формул:

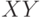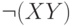0	0	0	1	1
0	1	0	1	1
1	0	0	1	1
1	1	1	0	0

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Операцию Штрих Шеффера называют антиконъюнкцией.

Стрелка Пирса эквивалентна отрицанию дизъюнкции:

Построим таблицы истинности для этих двух формул:

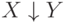0	0	0	1	1
0	1	1	0	0
1	0	1	0	0
1	1	1	0	0

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Операцию Стрелка Пирса называют антидизъюнкцией.

Импликация 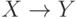эквивалентна дизъюнкции и отрицания :

Построим таблицы истинности для этих двух формул:

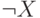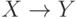0	0	1	1	1
0	1	1	1	1
1	0	0	0	0
1	1	0	1	1

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Эту эквивалентность , позволяющую избавиться от импликаций, часто используют при преобразовании формул.

Конъюнкция 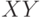эквивалентна отрицанию дизъюнкции отрицаний:

Построим таблицы истинности для этих двух формул:

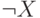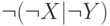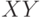0	0	1	1	1	0	0
0	1	1	0	1	0	0
1	0	0	1	1	0	0
1	1	0	0	0	1	1

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Дизъюнкция эквивалентна отрицанию конъюнкции отрицаний:

Построим таблицы истинности для этих двух формул:

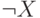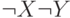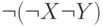0	0	1	1	1	0	0
0	1	1	0	0	1	1
1	0	0	1	0	1	1
1	1	0	0	0	1	1

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Почему на практике используется небольшое число функций?

Логических функций много, особенно функций многих переменных. Почему же мы знаем и оперируем небольшим числом функций? Связано это с тем, что одни функции можно выражать через другие, как мы видели на примерах. А можно ли любую функцию выразить через немногие, базисные функции? Ответ на этот вопрос положителен.

Каждую функцию от любого числа переменных можно представить в так называемой нормальной форме, в которой используются только три базисные функции – отрицание, конъюнкция и дизъюнкция.

Источник

Эквивалентные функции — формулы, свойства и примеры решений

В данной статье речь пойдет об основных понятиях эквивалентных функций, с помощью которых можно найти значение пределов. Понятие эквивалентности поменяется не только в высшей математике, но и в логике, психологии, при переводах с иностранных языков. Оно означает «равнозначность», «равносильность», «равенство».

Определение эквивалентных функций

Эквивалентные функции — это функции, имеющие одинаковое значение. Они могут представлять собой бесконечность малых и больших величин.

Функция может иметь такое понятие лишь при наличии предела. Следует понимать, что одна и та же функция принимает значение малой или большой до бесконечности лишь в единственной точке.

Теорема о замене функций эквивалентными в пределе частного

Если при x₁, стремящимся к x₂, f(x)

g₁(x) существует предел:

то существует и предел:

Доказательство

Допустим, что следствие этой теоремы часто применяемое. Если мы имеем частное, являющееся результатом произведения функций:

в этом случае, при нахождении предела, можно сделать замену этих функций на эквивалентные:

Выражения равны друг другу, это значит, что при существовании одного из таких пределов, применимо существование выражения, равного первому. Соответственно, если не существует такой предел, то не может существовать и второй.

Следует отметить, что можно делать замену как одной величины функции, так и нескольких одновременно.

Таблица эквивалентных функций

Ниже приведена таблица равнозначных функций и формул при t → 0. В данном случае величина t может представлять собой как переменную, так и до бесконечности малую функцию t = t(x) при x → x₀:

Эквивалентность при t → 0

Равенство при t → 0

a t – 1 = t ln a + 0(t)

(1 + t) b — 1 = bt + 0(t)

Всегда ли можно сделать замену функций эквивалентными?

Свойства замены функций равносильными доступны для дробных выражений с перемножаемыми величинами и произведений, где необходимо найти предел.

В этом случае величины в числителе или знаменателе допускается заменить равнозначными функциями. Если математическое выражение представляет собой сумму чисел, замену сделать нельзя.

Примеры решения пределов с помощью эквивалентных функций

Для сравнения рассмотрим несколько примеров.

Пример 1

Начнём решение, учитывая, что tg2x

3x при x → 0, тогда

Пример 2

Пусть arcsin x = t, тогда x = sin t и t → 0 при x → 0. Исходя из этого:

Значит, arcsin x

Пример 3

Решение: если sin (15x)

Для решения пределов можно использовать онлайн калькуляторы, размещенные на ресурсах в свободном доступе.

Источник