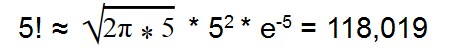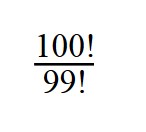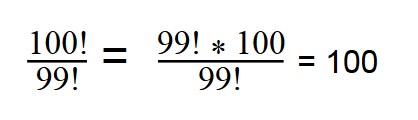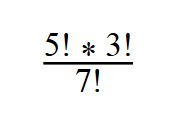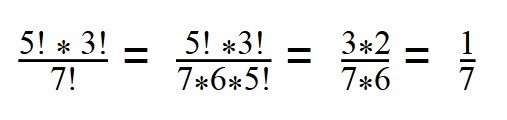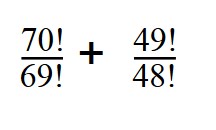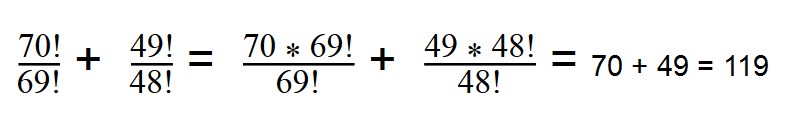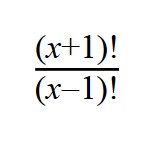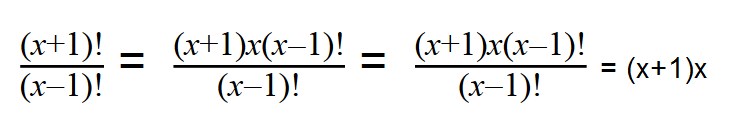Пределы с факториалами
Факториал числа $n!$ равен произведению чисел от 1 до $n$. Например, $5! = 1\cdot 2\cdot 3\cdot 4\cdot 5$. Для решения примеров на пределы с факториалами понадобится знать и понимать формулу разложения на множители. $$ (n+1)! = n!(n+1) \qquad (1) $$
Например, $5! = 4! \cdot 5 $, или $5! = 3! \cdot 4 \cdot 5$, а можно еще так $5! = 2! \cdot 3 \cdot 4 \cdot 5 $.
Основная суть идеи:
- Выносим наименьший факториал числа за скобки в числителе и знаменателе
- Сокращаем факториалы, избавляя тем самым предел от них
- Вычисляем предел подходящим способом
| Пример 1 |
| Вычислить предел с факториалами $\lim_\limits |
| Решение |
| Ответ |
| $$\lim_\limits |
| Пример 2 |
| Решить предел с факториалом $ \lim_\limits |
| Решение |
| Ответ |
| $$ \lim_\limits |
| Пример 3 | |||||||||||||||||||||||||||
| Найти предел $\lim_\limits | |||||||||||||||||||||||||||
| Решение | |||||||||||||||||||||||||||
| Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
- n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
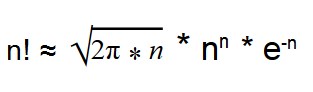 |
Рекуррентная формула
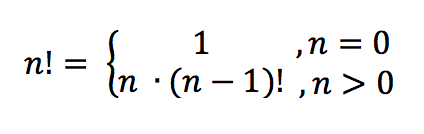 |
- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Источник
Пара слов о простых уравнениях с факториалами
Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел. Формула факториала: n! = 1 * 2 * … * n. Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала. Пример: 7! = 1 * … * 7 = 5040. Факторизация — разложение функции на множители.
Рекуррентная формула:
n! = 1 если n = 0
n! = (n — 1)! * n если n > 0
Комбинаторная интерпретация:
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга:
Позволяет не перемножать большие числа. Обычно необходим только главный член: n! ≈ √(2πт) * (n / e)^n
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее. Гамма-функция позволяет вычислять факториалы дробных чисел.
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0. Однако было решено, что в случае 0 результат будет равен 1. Из определения факториала следует соотношение (n-1)! = n! / n, откуда при n = 1 формально находим 0! = 1. Последнее равенство обычно принимают в качестве соглашения, хотя, как показано выше, оно следует из определения факториала для натуральных чисел при условии, что все значения функции связаны единым рекуррентным соотношением.
Факториал активно используется в различных разделах математики: комбинаторике, математическом анализе, теории чисел, функциональном анализе и др.
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем любая показательная функция или любая степенная функция, а также быстрее, чем любая сумма произведений этих функций. Однако степенно-показательная функция n^n растёт быстрее факториала, так же как и большинство двойных степенных, например exp(exp(n)).
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества
ABCD BACD CABD DABC
ABDC BADC CADB DACB
ACBD BCAD CBAD DBAC
ACDB BCDA CBDA DBCA
ADBC BDAC CDAB DCAB
ADCB BDCA CDBA DCBA
Не лишним будет сказать, что комбинаторная интерпретация факториала подтверждает целесообразность соглашения 0!=1 — количество перестановок пустого множества равно единице.
Факториал связан с гамма-функцией от целочисленного аргумента соотношением n! = Г(n + 1). Это же выражение используют для обобщения понятия факториала на множество вещественных чисел. Используя аналитическое продолжение гамма-функции, область определения факториала также расширяют на всю комплексную плоскость, исключая особые точки при n = -1,-2,-3.
Факториальные выражения появились ещё в ранних исследованиях по комбинаторике, хотя компактное обозначение n! предложил французский математик Кристиан Крамп только в 1808 году. Важным этапом стало открытие формулы Стирлинга, которую Джеймс Стирлинг опубликовал в своём трактате «Дифференциальный метод» (лат. Methodus differentialis, 1730 год). Немного ранее почти такую же формулу опубликовал друг Стирлинга Абрахам де Муавр, но в менее завершённом виде (вместо коэффициента √(2π) была неопределённая константа).
Стирлинг подробно исследовал свойства факториала, вплоть до выяснения вопроса о том, нельзя ли распространить это понятие на произвольные вещественные числа. Он описал несколько возможных путей к реализации этой идеи и высказал мнение, что: (1/2)! = √π / 2
Стирлинг не знал, что годом ранее решение проблемы уже нашёл Леонард Эйлер.
Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y)^n в многочлен).
Источник
Алгоритмы быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
Реализуем описанный алгоритм:
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K 2 -ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K 2 . Аналогично для K 3 , K 4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K 2 + N / K 3 + N / K 4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
График с линейной шкалой
График с логарифмической шкалой
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
Исходные коды реализованных алгоритмов приведены под спойлерами
Источник