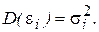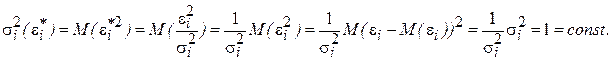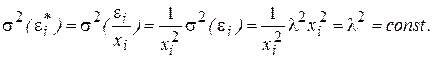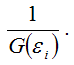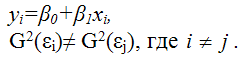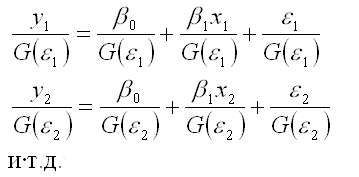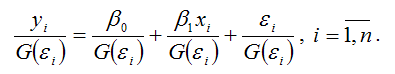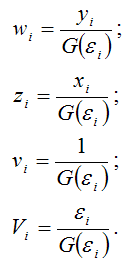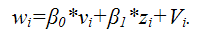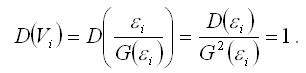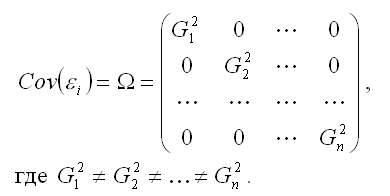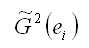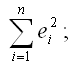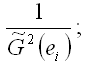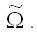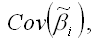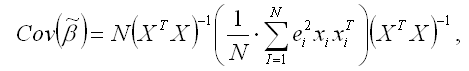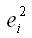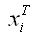Как избавиться от гетероскедастичности

Устранение гетероскедастичности

В случае, когда присутствие гетероскедастичности установлено, возникает необходимость преобразования регрессионной модели с целью устранения данного нежелательного явления. Вид преобразования зависит от того, известны или нет дисперсии случайных отклонений

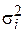
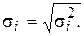
Предположим, что рассматриваемая модель гетероскедастична, и нам известны значения дисперсий остатков для каждого t-го наблюдения. При отсутствии автокорреляции это означает, что ковариационная матрица случайных отклонений V(e) = W — диагональная. В данном случае можно устранить гетероскедастичность, разделив каждое значение зависимой и объясняющих переменных на соответствующее стандартное отклонение Нормируя («взвешивая») переменные по σ_i, мы стремимся получить более точные оценки. В этом заключается суть так называемого взвешенного метода наименьших квадратов (ВМНК).

Для простоты изложения опишем ВМНК на примере парной регрессии:

Разделим каждый член модели (5.7) на известное σ_i:

(5.8)

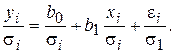
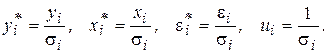
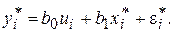
Введем обозначения Тогда уравнение модели (5.7) примет вид:

(5.9)

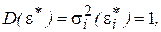
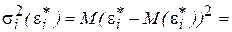
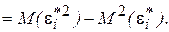
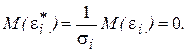
Полученное уравнение представляет собой регрессию без свободного члена, но с дополнительной объясняющей переменной U и с преобразованным случайным отклонением e*. Для преобразованной модели (5.9) дисперсия остатков т. е. имеет место гомоскедастичность. Действительно, можно записать Так как, согласно первой предпосылке МНК, математическое ожидание М(e_i) = 0, то Следовательно,

Таким образом, ковариационная матрица W в выражении (5.1) становится единичной, а сама преобразованная модель (5.9) – классической, к которой применим «обычный» МНК. Другими словами, в данном случае обобщенным методом наименьших квадратов для модели с гетероскедастичностью является взвешенный метод наименьших квадратов (ВМНК). «Взвешивая» каждый остаток 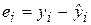с помощью коэффициента 1/σ_i, мы добиваемся равномерного вклада остатков в общую дисперсию и, в конечном счете, получения эффективных оценок параметров модели.

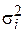
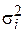
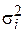
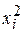
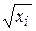
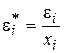
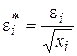
Рассмотренная выше процедура применения ВМНК предполагает, что фактические значения дисперсий нам известны. Как уже было отмечено, такое предположение реализуется крайне редко. Для применения ВМНК на практике необходимо сделать некоторые достаточно реалистические предположения о значениях . Например, может оказаться целесообразным предположить, что дисперсии остатков e_i пропорциональны значениям (стандартное отклонение остатков пропорционально независимой переменной) или значениям х_i. Тогда необходимым преобразованием будет деление уравнения регрессии (5.7) на х_i или соответственно, что позволит нам получить «преобразованные» случайные отклонения и , для которых выполняется условие гомоскедастичности. Например, определим дисперсию случайного члена для случая пропорциональности стандартного отклонения значениям независимой переменной (σ_i = σ(e_i) = lх_i, где l — коэффициент пропорциональности). В силу выполнимости предпосылки МНК имеем:

Несложно показать, что для отклонений 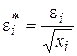также выполняется условие гомоскедастичности. Таким образом, для оценки преобразованных регрессий возможно применение МНК.

Рассматривая проведенные выше преобразования и их результаты, следует отметить, что применение обобщенного метода наименьших квадратов для моделей с гетероскедастичностью остатков заключается в минимизации суммы взвешенных квадратов отклонений выборочных данных от их оценок.

Автокорреляция

При анализе временных рядов часто приходится учитывать статистическую зависимость (коррелированность) наблюдений в разные моменты времени. Следовательно, в данном случае для регрессионных моделей Cov(e_i, e_j) ¹ 0, i ¹ j, т. е. третья предпосылка Гаусса-Маркова о некоррелированности остатков не выполняется. Такие регрессионные зависимости называются моделями с автокорреляцией (сериальной корреляцией) остатков. Для обобщенной линейной регрессионной модели с автокорреляцией ковариационная матрица случайных отклонений W не может быть диагональной.

Последствия автокорреляции остатков во многом сходны с последствиями гетероскедастичности (см. раздел 5.2). Среди них особенно следует выделить ухудшение прогнозных качеств моделей временных рядов.

Поскольку автокорреляция рассматривается в регрессионном анализе при использовании данных временных рядов, в дальнейших выкладках вместо символа i порядкового номера наблюдения будем использовать символ t отражающий момент наблюдения во времени (t = 1, 2, …, n). В экономических задачах более часто встречается так называемая положительная автокорреляция (Cov(e_{t — 1}, e_t) > 0 для соседних отклонений), нежели отрицательная автокорреляция (Cov(e_{t — 1}, e_t)

Дата добавления: 2016-06-02 ; просмотров: 2426 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

60. Устранение гетероскедастичности остатков модели регрессии

60. Устранение гетероскедастичности остатков модели регрессии

Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.

Наиболее простым методом устранения гетероскедастичности остатков модели регрессии является взвешивание параметров модели регрессии. В этом случае отдельным наблюдениям независимой переменой, характеризующимся максимальным среднеквадратическим отклонением случайной ошибки, придаётся больший вес, а остальным наблюдениям с минимальным среднеквадратическим отклонением случайной ошибки придаётся меньший вес. После данной процедуры свойство эффективности оценок неизвестных коэффициентов модели регрессии сохраняется.

Если для устранения гетероскедастичности был использован метод взвешивания, то в результате мы получим взвешенную модель регрессии с весами

Предположим, что на основе имеющихся данных была построена линейная модель парной регрессии, в которой было доказано наличие гетероскедастичности остатков

Рассмотрим подробнее процесс взвешивания для данной модели регрессии.

Разделим каждый член модели регрессии на среднеквадратическое отклонение случайной ошибки G(?i):

В общем виде процесс взвешивания для линейной модели парной регрессии выглядит следующим образом:

Для более наглядного представления полученной модели регрессии воспользуемся методом замен:

В результате получим преобразованный вид взвешенной модели регрессии:

Преобразованная взвешенная модель регрессии является двухфакторной моделью регрессии.

Дисперсию случайной ошибки взвешенной модели регрессии можно рассчитать по формуле:

Полученный результат доказывает постоянство дисперсий случайных ошибок преобразованной модели регрессии, т. е. о выполнении условия гомоскедастичности.

Главный недостаток метода взвешивания заключается в необходимости априорного знания среднеквадратических отклонений случайных ошибок модели регрессии. По той причине, что в большинстве случаев данная величина является неизвестной, приходится использовать другие методы, в частности методы коррекции гетероскедастичности.

Определение. Суть методов коррекции гетероскедастичности состоит в определении оценки ковариационной матрицы случайных ошибок модели регрессии:

Для определения оценок

используется метод Бреуше-Пайана, который реализуется в несколько этапов:

1) после получения оценок неизвестных коэффициентов модели регрессии рассчитывают остатки ei и показатель суммы квадратов остатков

2) рассчитывают оценку дисперсии остатков модели регрессии по формуле:

3) строят взвешенную модель регрессия, где весами являются оценка дисперсии остатков модели регрессии

4) если при проверке гипотез взвешенная модель регрессии является незначимой, то можно сделать вывод, что оценки матрицы ковариаций ? являются неточными.

Если вычислены оценки дисперсий остатков модели регрессии, то в этом случае можно использовать доступный обобщённый или взвешенный методы наименьших квадратов для вычисления оценок коэффициентов модели регрессии, которые отличаются только оценкой

Если гетероскедастичность остатков не поддаётся корректировке, то можно рассчитать оценки неизвестных коэффициентов модели регрессии с помощью классического метода наименьших квадратов, но затем подвергнуть корректировке ковариационную матрицу оценок коэффициентов

т. к. условие гетероскедастичности приводит к увеличению данной матрицы.

Ковариационная матрица оценок коэффициентов

может быть скорректирована методом Уайта:

где N – количество наблюдений;

X – матрица независимых переменных;

– квадрат остатков модели регрессии;

– транспонированная i-тая строка матрицы данных Х.

Корректировка ковариационной матрицы оценок коэффициентов

методом Уайта приводит к изменению t-статистики и доверительных интервалов для коэффициентов регрессии.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

11. Критерии оценки неизвестных коэффициентов модели регрессии

11. Критерии оценки неизвестных коэффициентов модели регрессии В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные

14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии

15. Оценка дисперсии случайной ошибки модели регрессии

15. Оценка дисперсии случайной ошибки модели регрессии При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой

18. Характеристика качества модели регрессии

18. Характеристика качества модели регрессии Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии

35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом

35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости

39. Модели регрессии, нелинейные по факторным переменным

39. Модели регрессии, нелинейные по факторным переменным При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных

40. Модели регрессии, нелинейные по оцениваемым коэффициентам

40. Модели регрессии, нелинейные по оцениваемым коэффициентам Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по

41. Модели регрессии с точками разрыва

41. Модели регрессии с точками разрыва Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)

44. Методы нелинейного оценивания коэффициентов модели регрессии

44. Методы нелинейного оценивания коэффициентов модели регрессии Функцией потерь или ошибок называется функционал вида Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических

46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии

46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все

57. Гетероскедастичность остатков модели регрессии

57. Гетероскедастичность остатков модели регрессии Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается

58. Тест Глейзера обнаружения гетероскедастичности остатков модели регрессии

58. Тест Глейзера обнаружения гетероскедастичности остатков модели регрессии Существует несколько тестов на обнаружение гетероскедастичности остатков модели регрессии.Рассмотрим применение теста Глейзера на примере линейной модели парной регрессии.Предположим, что

59. Тест Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии

59. Тест Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии Основным условием проведения теста Голдфелда-Квандта является предположение о нормальном законе распределения случайной ошибки ?i модели регрессии.Рассмотрим применение данного

61. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция

61. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция Автокорреляцией называется корреляция, возникающая между уровнями изучаемой переменной. Это корреляция, проявляющаяся во времени. Наличие автокорреляции чаще всего

62. Критерий Дарбина-Уотсона обнаружения автокорреляции остатков модели регрессии

62. Критерий Дарбина-Уотсона обнаружения автокорреляции остатков модели регрессии Помимо автокорреляционной и частной автокорреляционной функций для обнаружения автокорреляции остатков модели регрессии используется критерий Дарбина-Уотсона. Однако данный критерий

63. Устранение автокорреляции остатков модели регрессии

63. Устранение автокорреляции остатков модели регрессии В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков

Источник