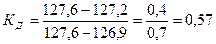Как избавиться от грубых погрешностей

Способы обнаружения и исключения грубых погрешностей

Грубая погрешность или промах – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором. К ним можно отнести:

— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;

— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например гирь;

— хаотические изменения параметров питающего СИ напряжения, например его амплитуды или частоты.

Грубые погрешности, как правило, возникают при однократных измерениях и обычно устраняются путем повторных измерений. Их причинами могут быть внезапные и кратковременные изменения условий измерения или оставшиеся незамеченными неисправности в аппаратуре. При многократных измерениях для обнаружения промахов используют статистические критерии.

Для выявления грубых погрешностей используются, например, критерий «трех сигм», критерий Романовского, критерий Шарлея, вариационный критерий Диксона и другие.

Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q 3S ,

где 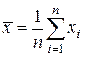— среднее арифметическое значение результатов наблюдений;

n – количество наблюдений или измерений.

Данный критерий надежен при числе измерений n > 20. 50.

Критерий Романовского применяется, если число измерений n 20). Тогда по теореме Бернулли число результатов, превышающих по абсолютному значению среднее арифметическое значение на величину К_ШS, будет n[l — Ф(К_Ш)], где Ф(К_Ш) — значение нормированной функции Лапласа для X = К_Ш. Если сомнительным в ряду результатов наблюдений является один результат, то n[1-Ф(К_Ш)] = 1. Отсюда Ф(К_Ш) = (n -1)/n.

Значения критерия Шарлье приведены в таблице1.2.

Таблица 1.2 – Значения критерия Шарлье

n
КШ	1,3	1,65	1,96	2,13	2,24	2,32	2,58

Пользуясь критерием Шарлье, отбрасывают результат, для значения которого в ряду из n наблюдений выполняется неравенство |х_i — х̅| > К_ШS.

Вариационный критерий Диксона удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд х₁, х₂, . . ., x_n (x₁ Z_q) = q. Значения Z_q приведены в таблице 1.3

Таблица 1.3 – Значения критерия Диксона

n	Zq при q, равном
0,10	0,05	0,02	0,01
0,68	0,76	0,85	0,89
0,48	0,56	0,64	0,70
0,40	0,47	0,54	0,59
0,35	0,41	0,48	0,53
0,29	0,35	0,41	0,45
0,28	0,33	0,39	0,43
0,26	0,31	0,37	0,41
0,26	0,30	0,36	0,39
0,22	0,26	0,31	0,34

Кроме рассмотренных критериев, существуют и другие, например критерии Граббса и Шовенэ.

Источник

Как избавиться от грубых погрешностей

Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей

n Уровень значимости α n Уровень значимости α 0.10 0.05 0.025 0.01 0.10 0.05 0.025 0.01 3 1.41 1.41 1.41 1.41 15 2.33 2.49 2.64 2.80 4 1.65 1.69 1.71 1.72 16 2.35 2.52 2.67 2.84 5 1.79 1.87 1.92 1.96 17 2.38 2.55 2.70 2.87 6 1.89 2.00 2.07 2.13 18 2.40 2.58 2.73 2.90 7 1.97 2.09 2.18 2.27 19 2.43 2.60 2.75 2.93 8 2.04 2.17 2.27 2.37 20 2.45 2.62 2.78 2.96 9 2.10 2.24 2.35 2.46 21 2.47 2.64 2.80 2.98 10 2.15 2.29 2.41 2.54 22 2.49 2.66 2.82 3.01 11 2.19 2.34 2.47 2.61 23 2.50 2.68 2.84 3.03 12 2.23 2.39 2.52 2.66 24 2.52 2.70 2.86 3.05 13 2.26 2.43 2.56 2.71 25 2.54 2.72 2.88 3.07 14 2.30 2.46 2.60 2.76

Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения X_ср и среднеквадратичного отклонения S для выборки нового объема n — 1.

Рассмотрим другой метод отсева грубых погрешностей для малой выборки [3]. В этом случае вычисляют статистику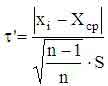

и полученный результат сравнивают с критическим значением, взятым из Таблицы 2 при соответствующих n и q = 1 — α.

Критические точки для отсева грубых погрешностей при малых выборках

n 1 — α = 0.90,
α = 0.10 1 — α = 0.95,
α = 0.05 1 — α = 0.99,
α = 0.01 3 1.41 1.41 1.41 4 1.64 1.69 1.72 5 1.79 1.87 1.96 6 1.89 2.00 2.13 7 1.97 2.09 2.26 8 2.04 2.17 2.37 9 2.10 2.24 2.46 10 2.15 2.29 2.54

Отсев грубых погрешностей можно производить и для больших выборок. Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике и в большинстве серьезных математических пакетов. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике.

Известно, что критическое значение τ_p (p — процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента t_{p, n-2} [4]: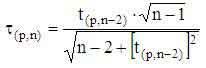
.

1. Микешина Н.Г. Выявление и исключение аномальных значений (обзор). «Заводская лаборатория» 1966, № 3, стр. 310.

2. Пустыльник Е.И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968.

3. Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. — М.: Наука, 1970.

4. Таблицы математической статистики. Большев Л.Н., Смирнов Н.В. — М.: Наука. Главная редакция физико-математической литературы, 1983. — 416 с.

Использована публикация: Львовский Е.Н. Статистические методы построения эмпирических формул: Учеб. пособие для втузов. — 2-е изд., перераб. и доп. — М.: Высш. шк., 1988. — 293 с. Стр. 23 — 25.

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди «Не укради»

Источник

Методы исключения грубых погрешностей

Грубая погрешность, или промах – это погрешность резуль­тата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные опе­ратором.

К ним можно отнести:

• неправильный отсчет по шкале измерительного прибора, про­исходящий из-за неверного учета цены малых делений шкалы;

• неправильная запись результата наблюдений, значений от­дельных мер использованного набора, например гирь;

• хаотические изменения параметров питающего СИ напряже­ния, например его амплитуды или частоты.

Корректная статистическая обработка выборки возможна только при ее однородности, т.е. в том случае, когда все ее члены принадлежат к одной и той же генеральной совокупно­сти. В противном случае обработка данных бессмысленна. «Чу­жие» отсчеты по своим значениям могут существенно не отли­чаться от «своих» отсчетов. Их можно обнаружить только по виду гистограмм или дифференциальных законов распределе­ния. Наличие таких аномальных отсчетов принято называть загрязнениями выборки , однако выделить члены выборки, при­надлежащие каждой из генеральных совокупностей, практиче­ски невозможно.

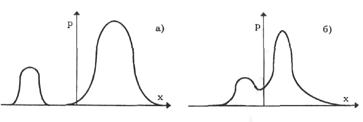
Если «свои» и «чужие» отсчеты различаются по значениям, то их исключают из выборки (рис.6.1,а). Особую неприятность дос­тавляют отсчеты, которые хотя и не входят в компактную группу основной массы отсчетов выборки, но и не удалены от нее на зна­чительное расстояние, – так называемые предполагаемые промахи (рис. 6.1,6).

Рисунок 6.1 – Проявление промахов на дифференциальном законе распределения вероятности

Отбрасывание «слишком» удаленных от центра вы­борки отсчетов называется цензурированием выборки. Это осуще­ствляется с помощью специальных критериев.

При однократных измерениях обнаружить промах не представ­ляется возможным. Для уменьшения вероятности появления про­махов измерения проводят два-три раза и за результат принимают среднее арифметическое полученных отсчетов. При многократных измерениях для обнаружения промахов используют статистиче­ские критерии, предварительно определив, какому виду распреде­ления соответствует результат измерений.

Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается общими методами проверки статистиче­ских гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдения х_i не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опро­вергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погреш­ность и его исключают.

Для выявления грубых погрешностей задаются вероятностью q (уровнем значимости) того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений.

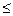
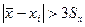
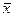
Критерий «трех сигм» применяется для результатов измере­ний, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q0,003, маловероятен и его можно считать промахом, если , где S_x – оценка СКО измерений. Величины и S_x вычисляют без учета экстремальных значений х_i. Данный критерий надежен при числе измерений n > 20-50.

Это правило обычно считается слишком жестким, поэтому ре­комендуется назначать границу цензурирования в зависимости от объема выборки: при 6 Данное правило также применимо только для нормального закона.

В общем случае границы цензурирования t_гр, S_х выборки зави­сят не только от объема n, но и от вида распределения. Назначая ту или иную границу, необходимо оценить уровень значимости q, т.е. вероятность исключения какой-либо части отсчетов, при­надлежащих обрабатываемой выборке.

Выра­жение для приближенного расчета коэффициента t_гр при уровне значимости q

• кругловершинных двухмодальных распределений с ε = 1,5, 3, являющихся композицией дискретного двузначного и нормального распределений;

• островершинных двухмодальных распределений с ε = 1,5, 6, являющихся композицией дискретного двузначного распределе­ния и распределения Лапласа;

• композиций равномерного и экспоненциальных распределе­ний с показателем степени α = 1/2 при ε = 1,8, 6;

• экспоненциальных распределений с ε = 1,5, 6.

Критерий Романовского применяется, если число измерений n β_т, то результат x_i считается промахом и отбрасывается.

Пример 6.3. При диагностировании топливной системы автомобиля ре­зультаты пяти измерений расхода топлива составили: 22, 24, 26, 28, 30 л на 100 км. Последний результат вызывает сомнение. Проверить по крите­рию Романовского, не является ли он промахом.

Значения критерия Романовского β = f(n)

q	n = 4	n = 6	n = 8	n = 10	n = 12	n = 15	n = 20
0,01 0,02 0,05 0,10	1,73 1,72 1,71 1,69	2,16 2,13 2,10 2,00	2,43 2,37 2,27 2,17	2,62 2,54 2,41 2,29	22,75 2,66 2,52 2,39	2,90 2,80 2,64 2,49	3,08 2,96 2,78 2,62

Найдем среднее арифметическое значение расхода топлива и его СКО без учета последнего результата, т.е. для четырех измерения. Они соответственно равны 25 и 2,6 л на 100 км.

Критерий Романовского свидетельствует о необходимости отбрасыва­ния последнего результата измерения.

Вариационный критерий Диксона удобный и достаточно мощ­ный (с малыми вероятностями ошибок). При его применении получен­ные результаты наблюдений записывают в вариационный возрастаю­щий ряд x₁, х₂, х_n (х₁ Z_p) = q. Значения Z_p приведены в табл. 6.2.

Пример 6.4. Было проведено пять измерений напряжения в электросети. Получены следую­щие данные: 127,1; 127,2; 126,9; 127,6; 127,2 В. Результат 127,6 В существенно (на первый взгляд) от­личается от остальных. Прове­рить, не является ля он промахом.

Составим вариационный ряд из результатов измерений напряжения в электросети: 126,9; 127,1; 127,2; 127,2; 127,6 В. Для крайнего члена этого ряда (127,6 В) критерий Диксона

Значения критерия Диксона

n	Zq при q, равном
0,10	0,05	0,02	0,01
0,68 0,48 0,40 0,35 0,29 0,28 0,26 0,26 0,22	0,76 0,56 0,47 0,41 0,35 0,33 0,31 0,30 0,26	0,85 0,64 0,54 0,48 0,41 0,39 0,37 0,36 0,31	0,89 0,70 0,59 0,53 0,45 0,43 0,41 0,39 0,34

Как следует из табл.6.2, по этому критерию результат 127,6 В может быть отброшен как промах лишь на уровне значимости q = 0,10.

Применение рассмотренных критериев требует осмотрительности и учета объективных условий измерений. Конечно, оператор должен ис­ключить результат наблюдения с явной грубой погрешностью и выпол­нить новое измерение. Но он не имеет права отбрасывать более или менее резко отличающиеся от других результаты наблюдений. В сомни­тельных случаях лучше сделать дополнительные измерения (не взамен сомнительных, а кроме них) и затем привлекать на помощь рассмотрен­ные выше статистические критерии. Кроме рассмотренных критериев, существуют и другие, например критерии Граббса и Шовенэ.

Источник