Как избавиться от интеграла

Избавиться от знака интеграла

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Какой смысл у знака определённого интеграла ?
Геометрический или аналитический или физический или всё вместе .

Избавиться от определённого знака в конце строки
Подскажите пожалуйста как избавить от знака вопроса в конце строки. Тобишь если он есть что бы.

Как выводить спецсимволы? Типа знака степени, знака корня и т.д.
Вы уж извините, что много тем создаю. Я не нашел.

Как сделать так чтобы в паскале после знака запятой оставалось только 4 знака?
Как сделать так чтобы в паскале после знака запятой оставалось только 4 знака? Например число.

Решение

Уважаемый мягко намекает вам о некорректности вашей формулировки «избавиться от знака интеграла». Такого понятия в математике нет. Есть «найти/взять определённый интеграл». Так что нет ни оффтопа, ни грубости. И пользуйтесь редактором формул — формулы не рассказывают.

Добавлено через 1 час 55 минут
А если по теме, нужно сделать замену переменных , чтобы пределы интегрирования были от 0 до 1, и попытаться свести к бета-функции. Тогда

Дальше нужно анализировать чётность-нечётность k. То, что k может быть только целым, видно из условия: подинтегральное выражение в указанных пределах может быть только 2

Источник

Сегодня вы поймёте, что такое интеграл в математике

(и в программировании)

Недавно мы разобрали, что такое знаки Σ и П в математике — это операции, которые, по сути, похожи на циклы в программировании. В одном случае мы складывали много чисел по определённому принципу, а в другом — умножали.

Сегодня посмотрим на интеграл ∫ — что это такое и какой цикл можно сделать из него.

Но сначала: что такое функция

Интегралы в математике всегда связаны с функциями, поэтому сначала поговорим про них.

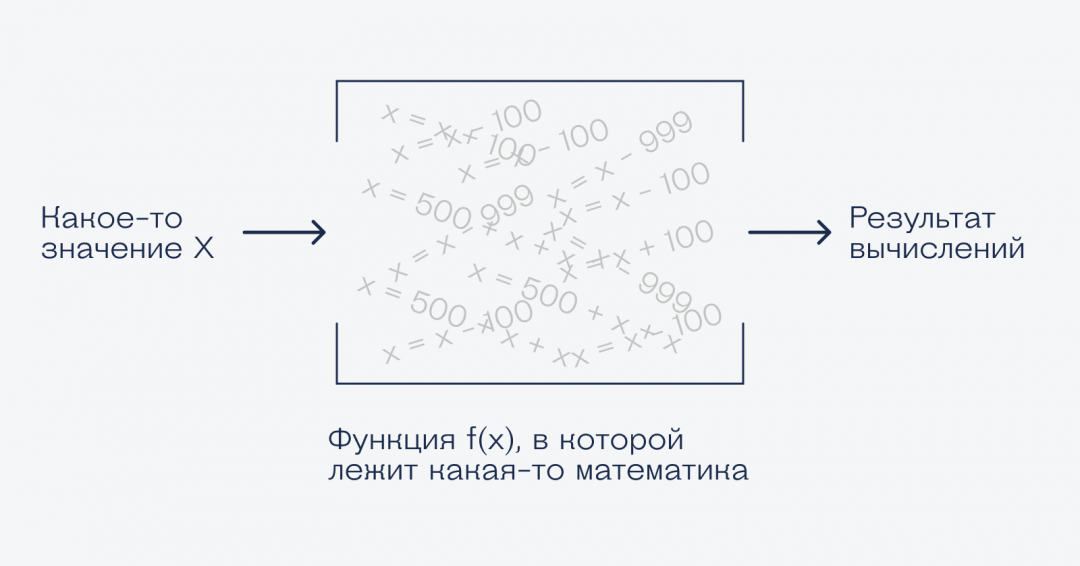
Функцию можно представить как «коробку с математикой». У тебя есть какая-то масса математических операций, ты их «запаковываешь» в функцию. Теперь ты можешь эту массу операций вызывать в своих математических выражениях одним действием.

У функции есть один или несколько аргументов — это те числа, к которым нужно применить массу математических операций. Можно представим, что мы засунули это число в коробку с математикой, потрясли и получили на выходе другое число.

Из школы вы наверняка помните функции sin() и cos() — синус и косинус. На вход им подаётся какое-то число, это число насилуют по теореме Пифагора, а на выходе получается дробное число от –1 до 1.

Функции можно засовывать в другие функции. Например, возьмём новую функцию f(x) и положим в неё выражение sin(x) + cos(x) . Это будет работать так:

1. Берется значение x.
2. Считается синус x.
3. Считает косинус x.
4. Результаты складываются.
5. Результат сложения отдаётся туда, где была вызвана функция.

Если посчитать f(x) для одного числа, получится другое число. Если посчитать f(x) от 100 чисел, получится 100 других чисел. А если непрерывно считать f(x) для бесконечного количества чисел, то получится бесконечное количество других чисел.

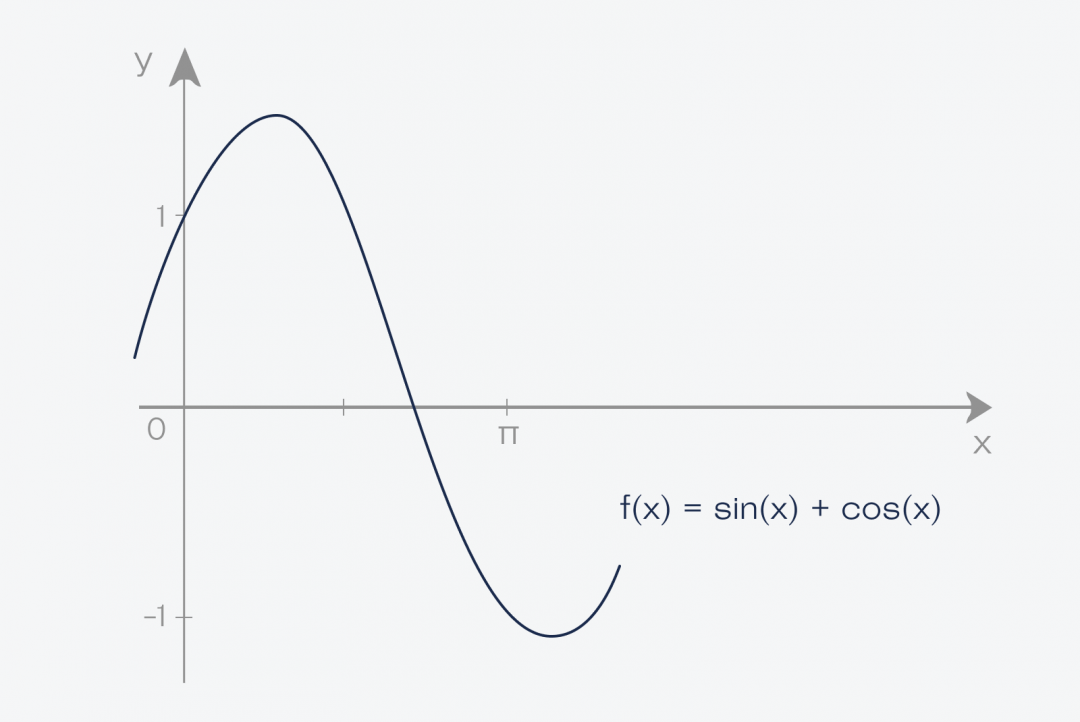
Если поставить эти числа по возрастанию x, то можно построить график функции y = f(x) . Это означает, что по горизонтали мы имеем все возможные значения x, а по вертикали — результат вычисления функции f(x) . Если каждый результат отметить точкой, получится линия:

Что такое интеграл

Итак, у нас есть некая функция, у неё есть числа на входе и числа на выходе. Эти пары чисел можно использовать для построения графика функции.

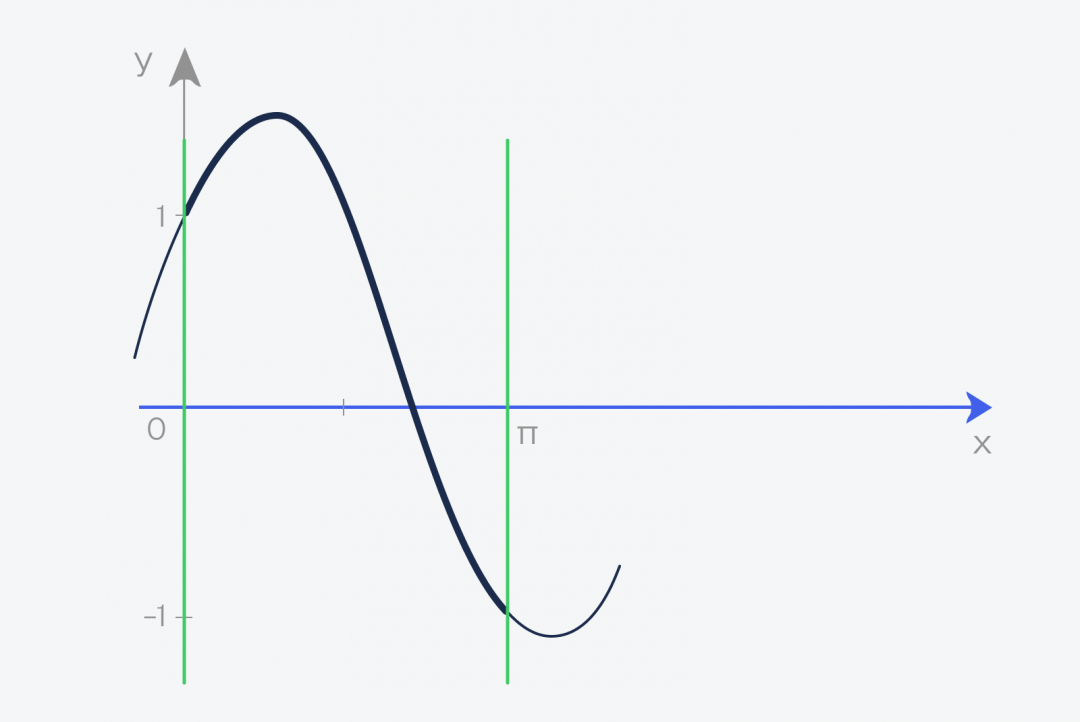
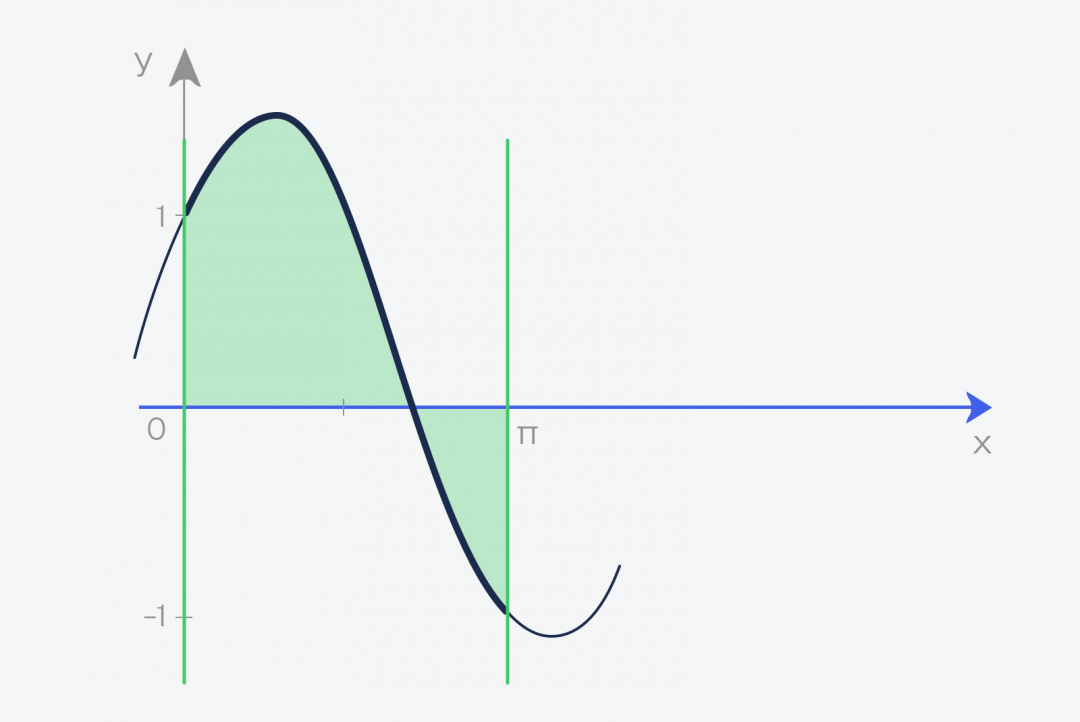
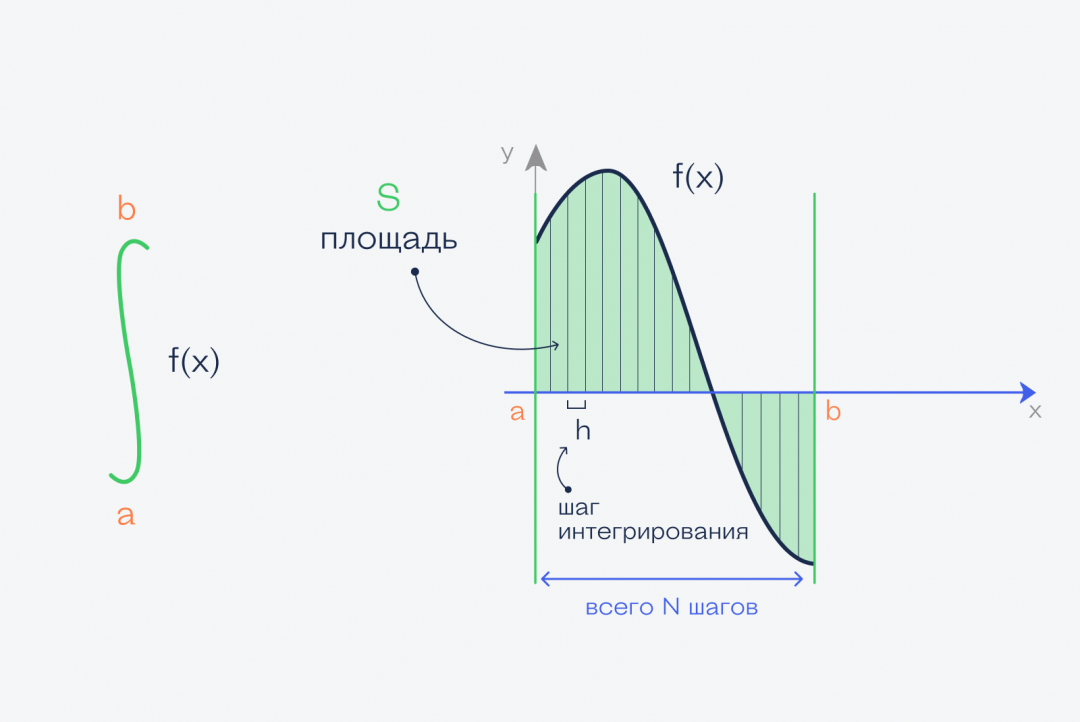
Теперь берём этот график функции и проводим две линии, которые ограничивают график. Получается фигура, которая сверху зависит от нашей функции, а с остальных сторон ограничена прямыми линиями и осью:

А теперь то, ради чего всё это затевалось:

✅ Площадь этой фигуры и есть интеграл функции f(x) = sin(x) + cos(x) на отрезке от a до b

В нашем случае мы считаем интеграл от нуля до числа пи — 3,1415926.

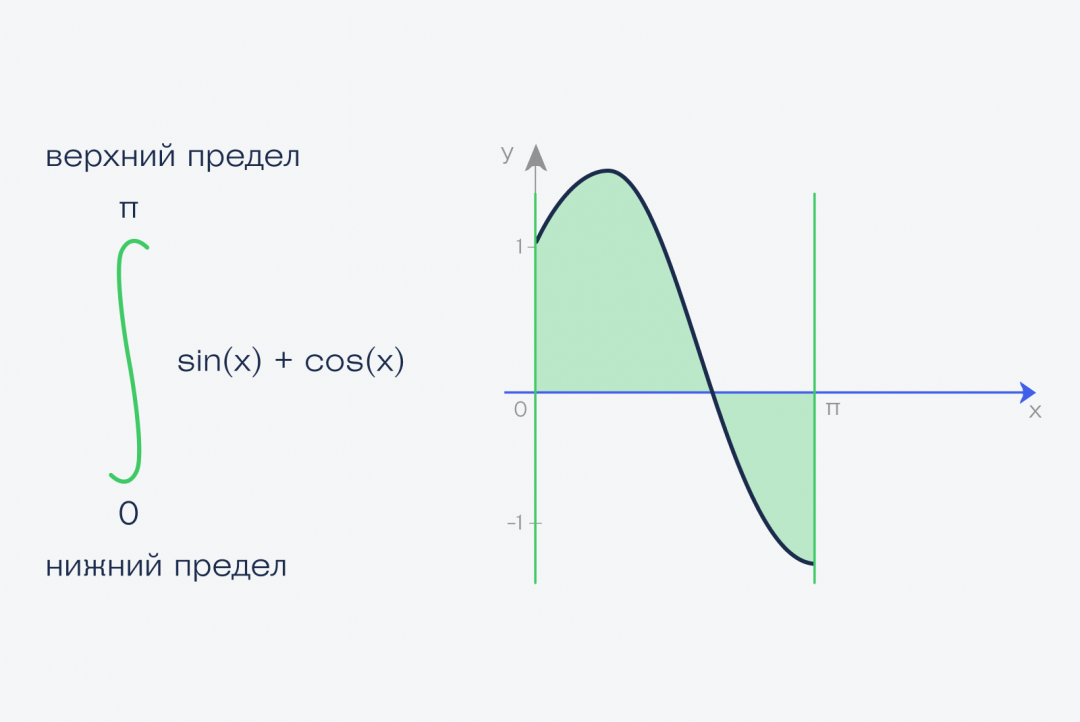
Это называется определённый интеграл. Определённый — это когда у нас определены начало и конец фигуры — в математике это называют пределами интегрирования. Записывается этот интеграл так:

В математике есть ещё неопределённые интегралы, у которых нет пределов интегрирования. Ими мы заниматься не будем, потому что ответом к неопределённому интегралу будет не конкретное число, а формула.

Зачем нужны интегралы в народном хозяйстве

Вы удивитесь, но в первую очередь интегралы нужны, чтобы находить площади и объёмы. В буквальном смысле: вот фигура, вот её описание в виде функции, проинтегрировали — узнали площадь. Будете, например, заливать бетоном красивую кривую дорожку — узнаете, сколько вам нужно бетона.

Интегралы нужны в математике и физике, это один из инструментов вычислений.

Если вы астрофизик, интеграл поможет вам рассчитать какие-нибудь свойства звёзд с течением времени. А математики говорят, что в интегралах не нужно искать практический смысл; их нужно любить, как мать, и почитать, как отца.

Как посчитать интеграл (то есть найти площадь)

Если бы у нас был прямоугольник, то всё просто: перемножаем высоту на ширину. Если бы была трапеция, тоже ещё как-то что-то можно. Но сверху у нас кривая, поэтому так сделать не получится. Решение придумали такое:

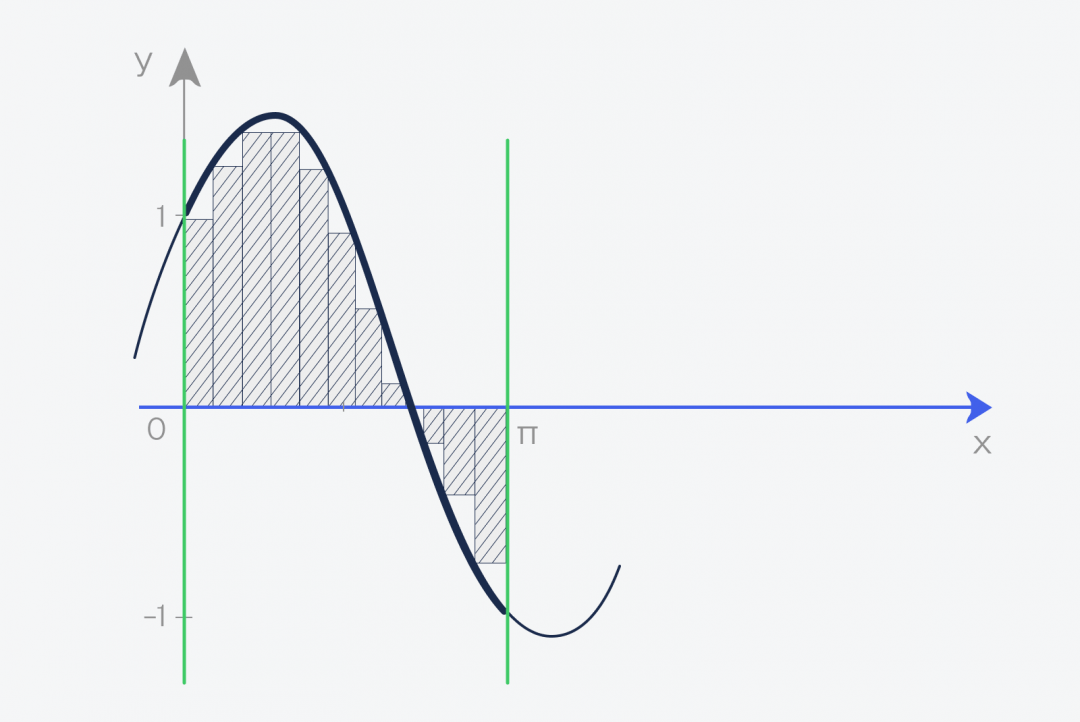
1. Разбиваем фигуру слева направо на много маленьких частей.
2. В каждой части рисуем маленький прямоугольник и находим его площадь.
3. Складываем площади всех прямоугольников и получаем общую площадь фигуры, а значит — значение интеграла.

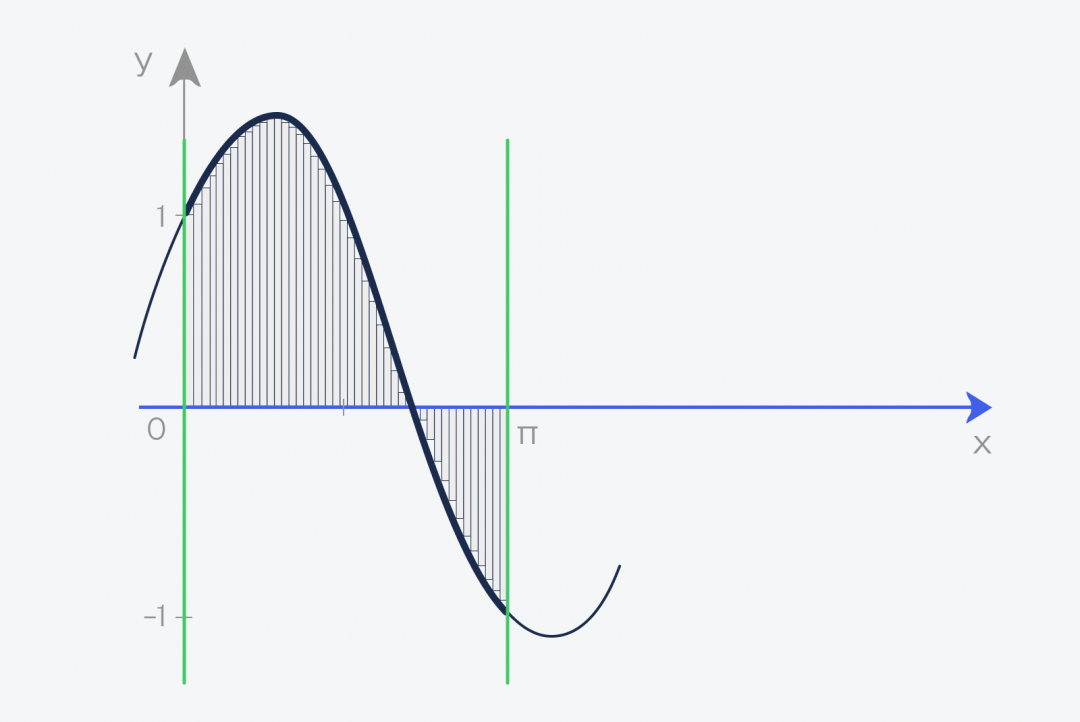
Минус такого подхода в том, что, как бы мы ни старались, прямоугольники не могут повторить все изгибы, и появится погрешность. С другой стороны, чем тоньше будут эти прямоугольники, тем точнее будет ответ. Получается, что наша задача — нарезать фигуру как можно тоньше.

Теперь задача становится намного проще: мы просто считаем площадь каждого прямоугольника и складываем их вместе. В таком виде задачу уже можно решить простым алгоритмом.

Пишем код

Раз нам нужно разбить интервал на много частей а потом с каждой из них сделать одно и то же, то это точно задача для цикла. Для этого нам понадобится шаг цикла — какой ширины будут наши прямоугольники, чтобы бы могли их одинаково перебирать.

Чтобы посчитать шаг, находим расстояние между конечной и начальной точкой и делим на желаемое количество прямоугольников (это будет нашей точностью интегрирования).

Общая логика работы будет такая:

1. Берём предыдущую точку и прибавляем к ней значение шага — так получаем новую точку.
2. Находим значение функции в новой точке — это будет высота прямоугольника.
3. Умножаем её на значение шага (ширину прямоугольника) — так получаем площадь прямоугольника.
4. Прибавляем значение площади к общей сумме всех площадей — так получаем значение интеграла.

На картинке — все исходные данные, а ниже — код, который считает интеграл. Смотрите на картинку и читайте комментарии: так будет ещё проще разобраться в коде:

Что дальше

Теперь этот код можно изменить так, чтобы он считал интеграл в любых пределах у любой функции. С точки зрения математики это не самый точный результат, но всё зависит от того, сколько точных знаков после запятой нам нужно.

В следующей серии продолжим разбираться со страшной математикой. Если есть пожелания для разбора — напишите в комментариях.

Источник

Разбираемся, как решать интегралы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос. Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения.

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Почему вы не знаете, как решать интегралы

• вычисление площади фигуры.
• вычисление массы тела с неравномерной плотностью.
• определение пройденного пути при движении с непостоянной скоростью.
• и др.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием. Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».

Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования. Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C». Пример решения неопределенного интеграла.

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

Таблица интегралов для студентов (основные формулы)

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Решение неопределенного интеграла

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Нескучные интегралы

Некоторые из вас, вероятно, видали на просторах сети эту задачку: какое число продолжает следующий ряд? Предлагался такой очевидный правильный ответ: Для тех, кому неочевидно, как он получен, предлагалось объяснение. Пусть (ну и 1 при x = 0, хотя неважно). Тогда каждый член ряда — это значение следующего интеграла в цепочке: Пока всё идёт хорошо, но тут внезапно: В принципе, этого достаточно, чтобы повеселить друзей-математиков, но мне захотелось узнать, как вообще считаются такие интегралы и почему получается такой смешной результат. Если кому-то ещё охота тряхнуть стариной и вспомнить матан с функаном, прошу читать дальше.

Начинает сказка сказываться

Для начала отдельно посмотрим на первый интеграл: Некоторое время назад я подумал: «Эй, я ещё не совсем забыл матан! Дайте-ка я возьму этот интеграл как неопределённый, а потом подставлю пределы. Наверняка пару раз по частям, и дело в шляпе.

Вот сейчас на бумажке всё решу без посторонней помощи». Хочу предостеречь вас: не повторяйте моей ошибки. Вас ждёт бессонная ночь, а потом вы заглянете в справочник и узнаете, что неопределённый интеграл не берётся в элементарных функциях. Для него даже специальную функцию ввели. Однако с данными конкретными пределами взять интеграл можно разными способами. Мы пойдём путём, который требует минимум базовых знаний (самое суровое — то же интегрирование по частям). Для начала сделаем внезапную замену: Вы спросите: откуда вообще это взялось и зачем нам ещё один интеграл, мало что ли? Спокойно, так надо (знакомые со свойствами преобразования Лапласа весело ухмыляются). Подставим замену в исходную формулу и поменяем порядок интегрирования: Внутри получился почти классический интеграл по dx, которым всех пугали у нас в физматшколе. Его можно взять и как неопределённый, дважды использовав формулу интегрирования по частям.

Тогда справа получится какая-то муть и ещё раз тот же самый интеграл, домноженный на что-то, и в результате можно будет решить уравнение относительно этого интеграла и получить ответ, а потом подставить пределы. Кому интересно, проделайте это сами, а я лениво запишу готовый результат: Ну а теперь совсем всё просто: это табличный интеграл из средней школы, который равен арктангенсу. В бесконечности пи-пополам, в нуле — ноль, вот мы и получили ответ. Интеграл, кстати, настолько хорош, что у него есть своё имя — интеграл Дирихле. По ссылке вы можете найти другие способы взять его.

Скоро сказка сказывается, а не скоро дело делается

Для следующего путешествия нам понадобятся четыре вещи: прямоугольная функция, косинусное преобразование Фурье, свёртка и теорема Парсеваля. Сперва скажу пару слов об этих замечательных штуках. Прямоугольная функция — это у нас будет такая ступенька вокруг нуля:

Значение 1/2 в точках разрыва нужно в основном для соблюдения свойств преобразования Фурье, в целом для нашей задачи оно непринципиально.

Косинусное преобразование Фурье. Для простоты мы немного отступим от математической точности и сформулируем грубовато. Для достаточно хорошей чётной функции f(x) выполняются такие соотношения:

Функция и называется косинусным преобразованием Фурье (FCT) от f(x) (её ещё называют образом f). То есть, косинусное преобразование от косинусного преобразования даёт снова исходную функцию f(x)!

Людям, знакомым с обработкой сигналов, хорошо известно, что FCT от прямоугольной функции — это . Это легко доказать, пользуясь вышеприведёнными формулами и школьными знаниями.

Так как прямоугольная функция за пределами промежутка [-a, a] равна нулю, то можно просто интегрировать cos(xt) dt по этому промежутку, тут простая замена переменной и табличный интеграл. Приведённое выше свойство говорит, что FCT от — это прямоугольная функция.

Свёртка — это ещё одна прекрасная штука, без которой не обходится обработка сигналов. Для двух функций f1(x) и f2(x) можно определить функцию-свёртку (обозначается звёздочкой) вот так:

У свёртки есть прекрасное свойство, за которое её любят: преобразование Фурье превращает её в умножение, а умножение — в свёртку. Если точнее, косинусное преобразование произведения двух хороших чётных функций есть свёртка их образов, делённая на корень из двух пи: .

Теорема Парсеваля — это очень крутое утверждение о равенстве энергии сигнала и его спектра, которое записывают по-разному в разных целях. Нам потребуется такая версия: для чётных и достаточно хороших функций .

Доселева Макар огороды копал, а нынече Макар в воеводы попал

Возьмём второй интеграл из нашей чудесной последовательности. Как многие уже догадались, мы воспользуемся теоремой Парсеваля и заменим множители на их FCT-образы:

• Чтобы дальше было проще, обозначим эту ступеньку под интегралом как F1(x) и нарисуем её график:

Первая прямоугольная функция под интегралом равна единице для аргументов меньше единицы и нулю для аргументов больше единицы. Поэтому ничто нам не мешает убрать её из интеграла, откорректировав пределы интегрирования: Под интегралом осталась ступенька высотой 3 и шириной 1/3.

Такой интеграл возьмёт даже третьеклассник: надо всего лишь умножить 3 и 1/3. От интеграла остаётся единица, и мы имеем искомое пи-пополам! Таким образом мы почти честно взяли второй интеграл из ряда. Кто желает сделать это совсем честно, тому придётся разобраться, что же такое хорошесть функции, и доказать, что наши функции хорошие.

Пойдём веселиться дальше и посмотрим на интеграл с тремя множителями. Чтобы применить теорему Парсеваля, мы теперь все множители со второго будем считать одним множителем: . С образом первого множителя всё уже понятно, а образ второго множителя, выражается через свёртку:

На первый взгляд жутковато. Но можно кое-чего повыносить, кое-чего посокращать и подставить нашу F1(x). Тогда получим: Внутренний интеграл — это просто прямоугольный фильтр, эдакий «блюр» для функции F1(x): мы просто для каждой точки усредняем все значения в окрестности плюс-минус одна пятая.

Можно опять же избавиться от прямоугольной функции, подшаманив пределы интегрирования. И со внешним интегралом сделаем такую же процедуру. Вот что получится в итоге: Слева график функции F2(x), которая на самом деле — сглаженная F1(x).

Нетрудно доказать, что после сглаживания функции по нормированному ядру её интеграл не меняется. Ну, вообще-то речь об интеграле от -∞ до +∞, но для чётной функции это верно и для интеграла от нуля. В данном случае ядром была ступенька от -1/5 до +1/5, умноженная на 5/2.

Площадь под ступенькой единица, значит, ядро нормировано. Тут тоже можно сравнить с блюром в фотошопе: после применения блюра картинка в целом не становится светлее или темнее. А раз так, то интеграл F2(x) в точности равен интегралу F1(x), то есть единице, поэтому и третий интеграл равен пи-пополам!

Дальше процедура во многом похожая. Четвёртый интеграл сгруппируем так: . Сначала теорему Парсеваля, для скобок свёртку, причём мы уже умеем выразить образ внутренней скобки через F2(x). Дальше всё то же самое, что в прошлый раз, и в результате получим:

Теперь мы уже имеем F3(x), которая на самом деле — сглаженная F2(x) с ядром шириной 2/7. Ядро нормировано, значит, интеграл F3(x) равен интегралу F2(x), то есть единице, и мы снова имеем пи-пополам!

Источник