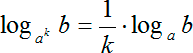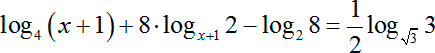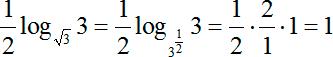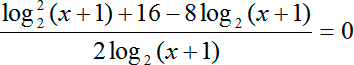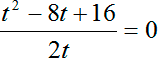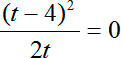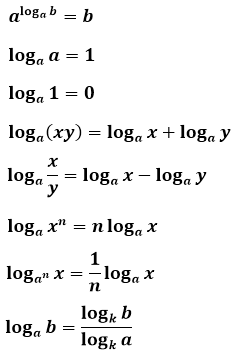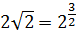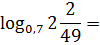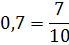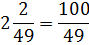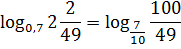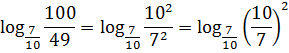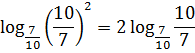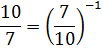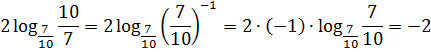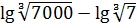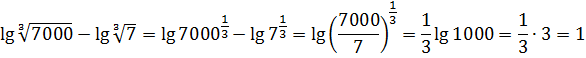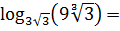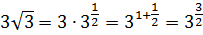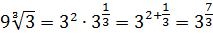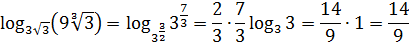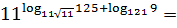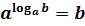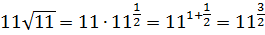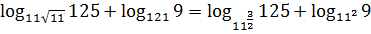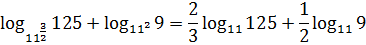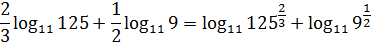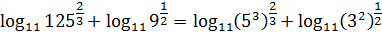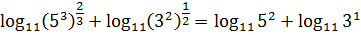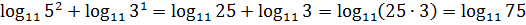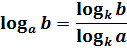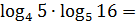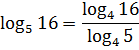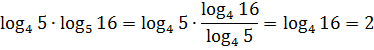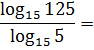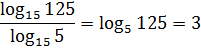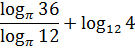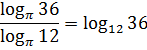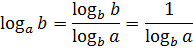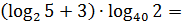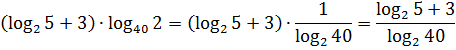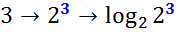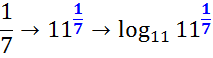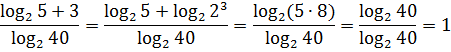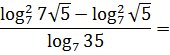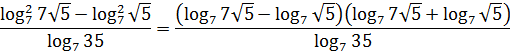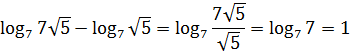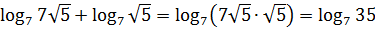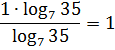Уравнения, квадратные относительно логарифма, и прочие нестандартные приемы
На уравнениях такого вида многие ученики «зависают». При этом сами задачи отнюдь не являются сложными — достаточно просто выполнить грамотную замену переменной, для чего следует научиться выделять устойчивые выражения.
В дополнение к этому уроку вас ждет довольно объемная самостоятельная работа, состоящая из двух вариантов по 6 задач в каждом.
Метод группировки
Сегодня мы разберем два логарифмических уравнения, одно из которых не решается «напролом» и требует специальных преобразований, а второе. впрочем, не буду рассказывать все сразу. Смотрите видео, скачивайте самостоятельную работу — и учитесь решать сложные задачи.
Итак, группировка и вынесение общих множителей за скобку. Дополнительно я расскажу вам, какие подводные камни несет область определения логарифмов, и как небольшие замечания по области определений могут существенно менять как корни, так и все решение.
Начнем из группировки. Нам нужно решить следующее логарифмическое уравнение:
log2 x · log2 ( x − 3) + 1 = log2 ( x 2 − 3 x )
В первую очередь отметим, что x 2 − 3 x можно разложить на множители:
Затем вспоминаем замечательную формулу:
Сразу же небольшое замечание: данная формула прекрасно работает, когда а, f и g — обычные числа. Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию:
f g fg будет положительным, следовательно, log a ( fg ) будет существовать, а вот log a f и log a g отдельно существовать не будут, и выполнить такое преобразование мы не сможем.
Игнорирование данного факта приведет к сужению области определения и, как следствие, к потере корней. Поэтому прежде чем выполнять такое преобразование, нужно обязательно заранее убедиться, что функции f и g положительные.
В нашем случае все просто. Поскольку в исходном уравнении есть функция log2 x , то x > 0 (ведь переменная x стоит в аргументе). Также имеется log2 ( x − 3), поэтому x − 3 > 0.
Следовательно, в функции log2 x ( x − 3) каждый множитель будет больше нуля. Поэтому можно смело раскладывать произведение на сумму:
log2 x log2 ( x − 3) + 1 − log2 x − log2 ( x − 3) = 0
На первый взгляд может показаться, что легче не стало. Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные:
a · b + 1 − a − b = 0
А теперь сгруппируем третье слагаемое с первым:
( a · b − a ) + (1 − b ) = 0
a (1 · b − 1) + (1 − b ) = 0
Заметим, что и в первой, и во второй скобке стоит b − 1 (во втором случае придется вынести «минус» за скобку). Разложим нашу конструкцию на множители:
a (1 · b − 1) − ( b − 1) = 0
А теперь вспоминаем наше замечательно правило: произведение равно нулю, когда хотя бы один из множителей равен нулю:
Вспоминаем, что такое b и а. Получим два простейших логарифмических уравнения, в которых останется лишь избавиться от знаков logи приравнять аргументы:
Мы получили два корня, но это не решение исходного логарифмического уравнения, а лишь кандидаты в ответ. Теперь проверим область определения. Для первого аргумента:
Оба корня удовлетворяют первому требованию. Переходим ко второму аргументу:
А вот здесь уже x = 2 нас не удовлетворяет, зато x = 5 вполне нас устраивает. Следовательно, единственным ответом будет x = 5.
Переходим ко второму логарифмическому равнению. На первый взгляд, оно существенно проще. Однако в процессе его решения мы рассмотрим тонкие моменты, связанные с областью определения, незнание которых существенно усложняет жизнь начинающим ученикам.
log0,7 ( x 2 − 6 x + 2) = log0,7 (7 − 2 x )
Перед нами каноническая форма логарифмического уравнения. Ничего преобразовывать не нужно — даже основания одинаковые. Поэтому просто приравниваем аргументы:
x 2 − 6 x + 2 = 7 − 2 x
x 2 − 6 x + 2 − 7 + 2 x = 0
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
Но эти корни еще не являются окончательными ответами. Нужно найти область определения, поскольку в исходном уравнении присутствуют два логарифма, т.е. учет области определения строго обязателен.
Итак, выпишем область определения. С одной стороны, аргумент первого логарифма должен быть больше нуля:
С другой — второй аргумент тоже должен быть больше нуля:
Эти требования должны выполняться одновременно. И вот тут начинается самое интересное. Безусловно, мы можем решить каждое из этих неравенств, затем пересечь их и найти область определения всего уравнения. Но зачем так усложнять себе жизнь?
Давайте заметим одну тонкость. Избавляясь от знаков log, мы приравниваем аргументы. Отсюда следует, что требования x 2 − 6 x + 2 > 0 и 7 − 2 x > 0 равносильны. Как следствие, любое из двух неравенств можно вычеркнуть. Давайте вычеркнем самое сложное, а себе оставим обычное линейное неравенство:
x x = −1, потому что x = 5 > 3,5.
Можно записать ответ: x = 1 является единственным решением исходного логарифмического уравнения.
Выводы из данного логарифмического уравнения следующие:
- Не бойтесь раскладывать логарифмы на множители, а потом множители раскладывать на сумму логарифмов. Однако помните, что разбивая произведение на сумму двух логарифмов, вы тем самым сужаете область определения. Поэтому прежде чем выполнять такое преобразование, обязательно проверьте, каковы требования области определения. Чаще всего никаких проблем не возникает, однако лишний раз перестраховаться не помешает.
- Избавляясь от канонической формы, старайтесь оптимизировать вычисления. В частности, если от нас требуется, чтобы f > 0 и g > 0, но в самом уравнении f = g , то смело вычеркиваем одно из неравенств, оставляя себе лишь самое простое. Область определения и ответы при этом никак не пострадают, а вот объем вычислений существенно сократится.
Вот, собственно, и все, что я хотел рассказать о группировке.:)
Типичные ошибки при решении
Сегодня мы разберем два типичных логарифмических уравнения, на которых спотыкаются многие ученики. На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений.
Дробно-рациональные уравнения с логарифмами
Сразу следует отметить, что это довольно коварный тип уравнений, в которых отнюдь не всегда сразу присутствует дробь с логарифмом где-то в знаменателе. Однако в процессе преобразований такая дробь обязательно возникнет.
При этом будьте внимательны: в процессе преобразований изначальная область определения логарифмов может существенно измениться!
Переходим к еще более жестким логарифмическим уравнениям, содержащим дроби и переменные основания. Чтобы за один короткий урок успеть больше, я не буду рассказывать элементарную теорию. Сразу перейдем к задачам:
4 log25 ( x − 1) − log3 27 + 2 log x − 1 5 = 1
Посмотрев на это уравнение, кто-то спросит: «При чем здесь дробно-рациональное уравнение? Где в этом уравнении дробь?» Давайте не будем спешить и внимательно посмотрим на каждое слагаемое.
Первое слагаемое: 4 log25 ( x − 1). Основанием логарифма является число, но в аргументе стоит функция от переменной x . С этим мы пока ничего сделать не можем. Идем дальше.
Следующее слагаемое: log 3 27. Вспоминаем, что 27 = 3 3 . Следовательно, весь логарифм мы можем переписать следующим образом:
log 3 27 = 3 3 = 3
Итак, второе слагаемое — это просто тройка. Третье слагаемое: 2 log x − 1 5. Тут тоже не все просто: в основании стоит функция, в аргументе — обычное число. Предлагаю перевернуть весь логарифм по следующей формуле:
Такое преобразование можно выполнить только если b ≠ 1. Иначе логарифм, который получится в знаменателе второй дроби, просто не будет существовать. В нашем случае b = 5, поэтому все в порядке:
2 log x − 1 5 = 2/log5 ( x − 1)
Перепишем исходное уравнение с учетом полученных преобразований:
4 log25 ( x − 1) − 3 + 2/ log5 ( x − 1) = 1
В знаменателе дроби у нас стоит log5 ( x − 1), а в первом слагаемом мы имеем log25 ( x − 1). Но 25 = 5 2 , поэтому выносим квадрат из основания логарифма по правилу:
Другими словами, степень в основании логарифма становится дробью спереди. А выражение перепишется так:
4 1/2 log5 ( x − 1) − 3 + 2/ log5 ( x − 1) − 1 = 0
У нас получилось длинное уравнение с кучей одинаковых логарифмов. Введем новую переменную:
А вот это уже дробно-рациональное уравнение, которое решается средствами алгебры 8—9 класса. Для начала разделим все на двойку:
( t 2 − 2 t + 1)/ t = 0
В скобках стоит точный квадрат. Свернем его:
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Никогда не забывайте про этот факт:
Вспоминаем, что такое t :
Избавляемся от знаков log, приравниваем их аргументы, и получаем:
Все. Задача решена. Но давайте вернемся к исходному уравнению и вспомним, что там присутствовали сразу два логарифма с переменной x . Поэтому нужно выписать область определения. Поскольку x − 1 стоит в аргументе логарифма, это выражение должно быть больше нуля:
С другой стороны, тот же x − 1 присутствует и в основании, поэтому должен отличаться от единицы:
Эти требования должны выполняться одновременно. Значение x = 6 удовлетворяет обоим требованиям, поэтому является x = 6 окончательным решением логарифмического уравнения.
Переходим ко второй задаче:
Вновь не будем спешить и посмотрим на каждое слагаемое:
log4 ( x + 1) — в основании стоит четверка. Обычное число, и его можно не трогать. Но в прошлый раз мы наткнулись на точный квадрат в основании, который пришлось выносить из-под знака логарифма. Давайте сейчас сделаем то же самое:
Фишка в том, что у нас уже есть логарифм с переменной x , хоть и в основании — он является обратным к логарифму, который мы только что нашли:
8 log x + 1 2 = 8 · (1/log2 ( x + 1)) = 8/log2 ( x + 1)
Следующее слагаемое — log2 8. Это константа, поскольку и аргументе, и в основании стоят обычные числа. Найдем значение:
То же самое мы можем сделать и с последним логарифмом:
Теперь перепишем исходное уравнение:
1/2 · log2 ( x + 1) + 8/log2 ( x + 1) − 3 − 1 = 0;
log2 ( x + 1)/2 + 8/log2 ( x + 1) − 4 = 0
Приведем все к общему знаменателю:
Перед нами опять дробно-рациональное уравнение. Введем новую переменную:
Перепишем уравнение с учетом новой переменной:
Будьте внимательны: на этом шаге я поменял слагаемые местами. В числителе дроби стоит квадрат разности:
Как и в прошлый раз, дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля:
( t − 4) 2 = 0 ⇒ t = 4;
Получили один корень, который удовлетворяет всем требованиям, поэтому возвращаемся к переменной x :
Все, мы решили уравнение. Но поскольку в исходном уравнении присутствовало несколько логарифмов, необходимо выписать область определения.
Так, выражение x + 1 стоит в аргументе логарифма. Поэтому x + 1 > 0. С другой стороны, x + 1 присутствует и в основании, т.е. x + 1 ≠ 1. Итого:
Удовлетворяет ли найденный корень данным требованиям? Безусловно. Следовательно, x = 15 является решением исходного логарифмического уравнения.
Напоследок хотел бы сказать следующее: если вы смотрите на уравнение и понимаете, что вам предстоит решать что-то сложное и нестандартное, по старайтесь выделить устойчивые конструкции, которые впоследствии будут обозначены другой переменной. Если же какие-то слагаемые вообще не содержат переменную x , их зачастую можно просто вычислить.
Вот и все, о чем я хотел сегодня рассказать. Надеюсь, этот урок поможет вам в решении сложных логарифмических уравнений. Смотрите другие видеоуроки, скачивайте и решайте самостоятельные работы, и до встречи в следующем видео!
Источник
Действия с логарифмами. Набиваем руку!
В данном уроке мы будем учиться работать с логарифмом на уже весьма и весьма приличном уровне. Поэтому для успешного решения примеров этого урока рекомендую погулять по ссылкам:
Почитайте, пока не поздно.) Почитали? Всё понятно! Отлично! Тогда движемся дальше.)
Теперь настал черёд завязывания более крепкой дружбы с логарифмами и, соответственно, решения серьёзных (в том числе сложных и нестандартных) примеров.
Чтобы не скакать из темы в тему, прежде всего я ещё разочек выпишу все основные свойства и формулы логарифмов. Вот они:
Это основной набор формул, необходимых для успешной работы с логарифмами практически на любом уровне сложности. Иногда в школе (и в некоторых продвинутых учебниках) дают больше формул, но в целом приведённого перечня для решения большей части примеров оказывается вполне достаточно. Эти формулы надо помнить! Но, ещё раз повторяю, не просто помнить, а уметь применять! Причём в обоих направлениях — как слева направо, так и справа налево. Вроде бы это всё и так понятно и очевидно, но… дальше всё поймёте.) Как надо помнить формулы, я вам вряд ли смогу подсказать, а вот как уметь применять — подробно расскажу и покажу в этом уроке.
Итак, продолжаем наши игры!
Все формулы. Все степени. Много дробей! Двоюродные и троюродные братья.
Ну что ж, теперь приступаем к работе со всеми формулами (кроме последней формулы перехода к новому основанию). Используем все свойства степеней и активно включаем в работу степени с отрицательными и дробными показателями. Поди сообрази, что, например,
Это уже не родные, а двоюродные и троюродные братья по степени получаются…)
Посему, если есть пробелы в степенях, то для начала милости прошу сюда:
Ну, а для тех, кто со степенями давно на «ты» — продолжаем.)
Пример 1
За что зацепиться? Хорошо, если сразу догадались, а если нет? Если нет, значит, перечитываем первый практический совет прошлого урока — переходим к обыкновенным дробям!
У нас в одну кучу намешаны десятичная дробь и смешанное число. Вот и перейдём к единообразию — к обычным дробям. А там, глядишь, и забрезжит свет в конце тоннеля…
Так, уже кое-чего проясняется: 49 с семёркой родня, а 100 — с десяткой:
Стало быть, по свойствам степеней можно записать:
Ну, вот и спасительный лучик света! Выносим двойку за логарифм и получаем:
Уже всё стало выглядеть гораздо симпатичнее. Всё бы ничего, только основание 7/10 и аргумент 10/7 у нас записаны кверху ногами. Что делать? Да свойства степеней вспомнить! На этот раз — с отрицательным показателем:
И снова выносим показатель степени (минус единицу) за знак логарифма, переворачиваем аргумент и получаем:
Готово дело.) Теперь пробуем самостоятельно:
А теперь вовлекаем в наш увлекательный процесс корни. То есть, не что иное, как… степени с дробными показателями. Да-да!
Пример 2
Надеюсь, вы не забыли, что lg — это просто логарифм по основанию 10? Или десятичный логарифм? Пример достаточно простой, без заморочек. Надо всего лишь вспомнить, что корень кубический из 7000 — это 7000 1/3 . С семёркой — аналогично. А дальше по формуле разности логарифмов да по формуле деления степеней. Получим:
Вот так вот. Здесь мы снова перешли к обычным дробям. Но не от десятичных дробей или смешанных чисел, а от корней. В этом безобидном примере вполне можно было бы и без дробей обойтись, работать напрямую с корнями, но в более сложных примерах корни могут вконец запутать. Как, например, вот в таком примерчике:
Пример 3
С чего начать? И тройка есть, и девятка. Правда, три в квадрате — это и будет девятка… Но в примере ещё и корни разных степеней смешались в кучу — квадратный и кубический! Ужас… Но паниковать и сдаваться рано. Перейдём-ка от корней к степеням с дробными показателями! Распишем девятку как 3 2 . А там, того гляди, всё и наладится.)
Верные мысли! Итак, по свойствам степеней для основания и для аргумента мы можем записать:
Вот всё и прояснилось.) Оба числа — и основание, и аргумент — оказались… родственниками! По тройке.) Только совсем уж дальними. Даже не троюродными, а десятиюродными братьями: основание — это три в степени 3/2, а аргумент — та же тройка, но в степени 7/3… Тем не менее факт остаётся фактом — родство по степени (хоть и очень дальнее) установлено. Вот и все формулы и свойства заработали! Выносим наши дробные показатели из за знак логарифма и аккуратно считаем:
Вот так. Здесь уже, конечно, немножко повозиться со степенями пришлось. А что делать… Так что не стесняемся переходить от корней к дробям! И всё получится. Обязательно.)
Вот вам и очередные практические советы:
При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями.
При наличии корней переходим от корней к степеням с дробными показателями.
Что ж, пришла пора разгрызть и какой-нибудь особо крепкий орешек. Как, например, вот такой примерчик:
Пример 4
Опять же, с чего начинать? Если имеете хоть малейшее представление — флаг вам в руки. Вперёд и с песнями, как говорится.) Если понятия не имеете — подключаем зелёные практические советы и размышляем синим цветом. Примерно так:
«Ух, наворотили… Кошмар! Напролом явно не решается, надо сначала как-то преобразовывать пример. Но — как? Будем вспоминать практические советы.
1. Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.
Где здесь дроби? Дробей не видно. Ладно, этот пункт пока пропустим. Что там у нас ещё есть? Вот это:
2. Степени популярных чисел надо знать. В лицо! При наличии в примере разных чисел пытаемся найти «братьев по степени».
Так, кое-какая зацепочка уже появилась… 121 — это 11 в квадрате. Ещё можно расписать 125 как 5 в кубе и 9 как 3 в квадрате, но 5 и 3 — никакие не братья и не сёстры по степени. Пригодится или нет — пока непонятно, но к сведению примем. Поехали дальше.)
3. Любую степень можно записать множителем перед логарифмом. И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.
Коэффициентов в нашем примере нет, логарифмы и так чистые. Отметаем этот совет. Что у нас там ещё припасено?
4. Всегда прикидываем, нельзя исходное выражение преобразовать под какую-нибудь готовую формулу?
Вот и прикидываем: на что похож внешний вид нашего примера? Ну же? Ну, конечно! На самую первую формулу — основное логарифмическое тождество! Единственная формула, где логарифм тусуется в показателе степени.
С ним мы пока что ни разу не работали. Что ж, поработаем! Попробуем преобразовать наш пример под эту формулу: других вариантов как-то выкрутиться у нас просто нет!
Но в формуле в показателе стоит один логарифм! А у нас — сумма. Что нам мешает сложить логарифмы по соответствующей формуле суммы? Основания мешают! Они… они — разные! Ну-ка, может, ещё не все практические советы у нас использованы? Вспоминаем:
5. При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями. При наличии корней переходим от корней к степеням с дробными показателями.
Так, ну дробей в нашем примере нету, это видно. А вот корень в основании — преобразуем. Вот так:
А во втором логарифме в основании тоже стоит 11, только в квадрате… Уже кое-какие проблески! Выпишу-ка я показатель отдельно, дабы не запутаться… С учётом наших размышлений.)
Уже лучше. Теперь выносим показатели степеней из оснований перед логарифмами (не забыть бы перевернуть…):
Великолепно! Основания логарифмов выровнялись! Только вот новая беда… Коэффициенты появились… Хотелось бы сложить логарифмы, ан нет, не канает… Так стоп! Чего же я туплю-то! Можно же их по другой формуле спрятать вовнутрь!
Ну вот. Уже идеально для формулы сложения! Только внутри логарифмов что-то несусветное стало твориться. Не беда, перейдём к маленьким числам: зря, что ли, мы 125 и 9 в виде степеней пятёрки и тройки расписывали?
Пока всё чин-чинарём. Теперь, по правилам действий со степенями, можно записать:
Вот, практически, и всё. Досчитываем наш показатель по формуле сложения логарифмов:
Пример становится всё лучше и лучше! Возвращаемся к нашему исходному примеру, вставляем в него наш преобразованный показатель и получаем ответ!
Йес. Ничего себе, примерчик, однако ж…»
Вот такой пример. Запутанный, да, я не спорю. И зачем я так детально его разобрал? С практическими советами, мыслями… Мог бы и в пару строк уложиться… Дело в том, что разбор одного конкретного примера — занятие бесполезное. Не попадётся он. А вот разъяснить на конкретном примере, как именно надо выкручиваться в любом (да-да, любом!) задании — совсем другое дело!
Главное в этом разборе — подход. Мы применяем весь наш арсенал инструментов к конкретному примеру. Пробуем поочерёдно все инструменты, как ключики к замку. Что-то срабатывает, а что-то нет. Это не страшно и не смертельно. Не подошло — пробуем что-то другое! Что-то обязательно подойдёт! Сложные и запутанные задания именно так и решаются. И никак иначе.)
Конечно, с опытом всё будет делаться гораздо короче и какие-то шаги будут в уме делаться и вообще пропускаться. За ненадобностью. Тут практика рулит. Тренироваться и решать надо. Используя изложенный здесь подход. И тогда всё получится. Обязательно!
Формула перехода к новому основанию. Немного приколов… И немного формул сокращённого умножения.
Поднимаемся ещё на ступень повыше. Запускаем теперь в дело самую последнюю формулу из нашего списка — это формула перехода к новому основанию. Вот она:
В чём суть этой формулы, когда она применяется и как именно она работает? Объясняю по пунктам.
Формула эта применяется, когда основания логарифмов — разные. Но не просто разные, а ещё и не родственные по степени! Которые друг в друга через простую степень не превращаются. Скажем, 2 и 3. Или 5 и 7. Заметьте, что нам уже встречались разные основания у логарифмов в одном и том же примере, но там или всё и так славненько срасталось, или переход был через степени. Например, если основания логарифмов 1/125 и 25, то можно догадаться, что это родня! По пятёрке. Ибо 1/125 = 5 -3 , а 25 = 5 2 . Не так очевидно, конечно, но и мы уже всё-таки на серьёзном уровне с вами. А дальше дело техники: выносим показатели за логарифмы и — вперёд.
Но если основания не родственные, а без выравнивания оснований в примере никак, то выход только один — работать по этой формуле.
Запомнить её очень легко. По шагам:
1) Слева пишем логарифм, основание которого нам не нравится. Справа рисуем черту дроби.
2) В числитель пишем логарифм числа b, но уже по новому основанию k. Какому именно основанию? А какому угодно! В том-то весь и фокус! Естественно, тому, которое нам удобнее. Кроме единицы, разумеется.)
3) В знаменатель пишем логарифм старого основания a по тому же новому основанию k.
Обратите внимание на саму структуру формулы: слева в основании буквы k вообще нет! В этом-то и вся фишка! Это означает, что новому логарифму мы можем выбрать какое угодно основание. Обычно выбирают то, которое нам удобно в конкретном примере. Если, скажем, в примере куча логарифмов по основанию 3 и затесался один по основанию 7, то его и менять будем. На тройку.
А в знаменатель пишем логарифм старого основания. Так уже математика требует. В результате логарифм со старым основанием исчезает из примера. Вот и всё. Вот и вся суть формулы перехода. Ну что, посмотрим на формулу перехода в действии?
Пример 5
Что тут можно увидеть? Ну, во-первых, разные основания. Причём не родственные: из четвёрки пятёрку простым возведением в степень никак не получить. Во-вторых, наблюдаем произведение логарифмов. Такой формулы в наших свойствах нету. Не путаем с логарифмом произведения! Или с суммой логарифмов… Что же делать? Первым делом перейдём к одному основанию. Что-то же делать всё равно надо! К какому основанию пойдём? Ну, ясное дело, что не к 30 или 1,234. У нас на выбор два варианта — либо к четвёрке, либо к пятёрке. В данном примере абсолютно без разницы, к чему переходить. Давайте к четвёрке пойдём: всё-таки число поменьше.) Итак, первый логарифм не трогаем (у него и так основание четыре), а вот второй логарифм превращаем по формуле перехода в дробь:
Всё. Логарифм по основанию 5 из примера благополучно исчез, и в основаниях остались только четвёрки. Вставляем полученную дробь в наш пример, упрощаем и считаем:
Вот так. Откуда же я узнал, что надо переходить к другому основанию? Ведь я мог и что-то ещё замутить. Скажем, log516 расписать как
и дальше как-то ещё выкручиваться. Да. Можно. Но с богатым опытом приходит уже так называемое математическое чутьё на формулы и преобразования.) Когда в уме наперёд уже умеешь просчитывать, к чему может привести тот или иной манёвр и не идёшь по заведомо негодному пути.
Вот вам очередной практический совет на данную тему.
Если перед вами сложное логарифмическое выражение, в котором основания логарифмов разные, то первым делом пробуем сделать их одинаковыми. Или через степени или по формуле перехода. Очень часто этот манёвр срабатывает проясняет дальнейшую ситуацию.
А теперь рассмотрим один фокус на формулу перехода, который частенько любят проделывать составители примеров. По-другому эту фишку даже и не назовёшь. Настолько элементарна, а в тупик может поставить даже отличника!
Пример 6
Основания уже одинаковые, но формулы деления логарифмов не существует, да… Можно, конечно, сообразить, что 125 = 5 3 и старым добрым способом, но что делать, если внутри логарифмов сидит что-нибудь более навороченное? Вот и впадают в ступор…
Здесь же достаточно всего лишь разглядеть формулу перехода к новому основанию. Вернее, не просто формулу, а её правую часть! И, если запустить эту формулу справа налево, то сразу получим:
И все дела! Да-да! Это ответ.)
Частенько эту фишку применяют с какими-нибудь совершенно дикими основаниями. На испуг берут, типа.) Как, например, вот такое задание:
Пример 7
В основании число «пи», как тут не испугаться… Однако, если догадаться, что наша ужасная дробь — всего лишь правая часть формулы перехода к новому основанию и сработать справа налево, то получим всего-навсего:
Вот и всё. И нету больше никакого «пи».) А уж сложить парочку логарифмов с одинаковыми основаниями — пустяшное дело. Не пример, а одно удовольствие:
Вот такой вот приёмчик. Теперь, надеюсь, не растеряетесь, в случае чего.)
Рассмотрим ещё одну распространённую фишку с формулой перехода. Вернее, её частный случай.
Что произойдёт, если за новое основание мы возьмём аргумент логарифма? Давайте посмотрим!
Во как! Оказывается, если поменять местами a и b, то наш новый логарифм станет всего лишь обратным к старому! Весьма и весьма полезная формулка. Имеет смысл запомнить.) Решим примерчик и на эту тему:
Пример 8
Что делать будем? Скобки раскрывать? Можно, конечно, но пример явно намекает на более элегантное преобразование. Перейдём в логарифме по основанию 40 к основанию 2. Двойка чем-то привлекательнее, чем сорок, не находите?) Поскольку в аргументе логарифма стоит также двойка, то при переходе к основанию 2 достаточно просто перевернуть этот логарифм. И все дела.)
И что дальше? Куда пристегнуть тройку? А дальше новый фокус! Дело всё в том, что мы не можем напрямую сложить логарифм и число. Но зато логарифмы между собой — запросто! Как выкрутимся? А сделаем-ка из тройки… логарифм! Да-да! Для этого сначала выберем ему основание. Вариантов выбора много, но я предлагаю выбрать 2. Думаю, возражений не будет?)
А дальше пишем вот такое простое равенство:
Всё легко и просто: тройка уходит показателем в степень нашего выбранного основания. Сама цепочка превращений выглядит вот так:
1) Вместо тройки пишем степень с выбранным основанием 2 и показателем, равным этой самой тройке.
2) Берём логарифм от этой степени по тому же самому основанию 2.
Конечно, можно было бы и сразу тройку на логарифм заменить, благо здесь числа совсем простые, но лучше запомнить эту простую цепочку. А то придётся где-нибудь, к примеру, превращать в логарифм по основанию 11 число 1/7… А по цепочке всё совсем элементарно:
Просекли фишку? Тогда возвращаемся к нашим баранам и дорешиваем:
Да… Кто бы мог подумать.)
Конечно, в числовых выражениях этот приёмчик с превращением числа в логарифм достаточно экзотичен. Но вот в логарифмических уравнениях и неравенствах он применяется на полную катушку! Имейте его в виду.)
Заметьте, что обычно мы стараемся поступать наоборот — упрощать всякие ужасы типа дробей, корней, синусов да логарифмов. Доводить их, по возможности, до конечного числа. А тут — наоборот, из числа делаем логарифм. Что хотим, то и творим! Так что математика — на самом деле весьма и весьма творческая наука! Во многом даже искусство.)
При необходимости любое число можно превратить в логарифм по любому основанию (кроме единицы, конечно).
Осталось разобраться с совсем уж хардкорными примерами. Где и так пробуешь и сяк, но не упрощается он никак! На такие примеры есть своё особое секретное оружие.) Срабатывает безотказно. Если уметь грамотно им пользоваться, конечно. Как вам такой примерчик!
Пример 9
За что зацепиться? Все основания уже одинаковые (семёрка), но это особо не спасает. Кстати, обращаю ваше внимание на весьма и весьма частый косяк. В числителе стоят квадраты логарифмов. Именно самих логарифмов, а не их аргументов! Это означает, что вынести двойки из логарифмов наружу мы не имеем права! Не там двойки стоят… Стало быть, уже привычных нам логарифмических формул, готовых к употреблению, нету. Что же делать?
Спокойно! Без паники! Никто и никогда не может гарантировать, что сразу влёт всё решится.) К сожалению…
Чтобы расправиться с этим злым примером, забудем на минутку про логарифмы и плавненько переместимся в седьмой класс. Формулы сокращённого умножения не забыли, надеюсь? А теперь внимательно присматриваемся к нашему примеру. Что ещё, кроме логарифмов, в нём можно увидеть? Разность… Разность ква… Ну, конечно! Разность квадратов! Такая родная и до боли знакомая формула:
Правда, в применении к логарифмам. Ну и что из этого? Ведь в формуле под буковками a и b может скрываться всё что угодно — и логарифмы, и синусы, и степени — любые выражения! Формула всё равно сработает!
Итак, заменяем наш числитель на произведение скобок по формуле разности квадратов:
Вот и всё встало на свои места! И все формулы заработали! Решать пример стало одно удовольствие.)
В первых скобках (разность) получается:
Во вторых скобках (сумма) будет:
Вставляем в пример наши промежуточные результаты, сокращаем и получаем:
Простенько и со вкусом.) Здесь-то всё ясно. Но в тревожной боевой обстановке ЕГЭ подобный пример может и в ступор вогнать. Дело всё в том, что большинство учеников подсознательно пытаются решить пример в том формате, в котором он задан. Например, если задан пример на логарифмы, то мы с головой погружены в логарифмы и варимся только в них, а вынырнуть на поверхность да оглядеться вокруг — не можем. С тригонометрией аналогично — решаем пример только в рамках тригонометрии. И, в случае чего, не можем напрячься и выскочить из этих жёстких рамок… А надо уметь! Хотя бы иногда.)
Посему очередной по счёту практический совет:
Замороченные примеры проверяем на алгебру седьмого класса — разложение на множители, формулы сокращённого умножения и т.п.
Ещё из той же оперы для самостоятельного решения:
Ну что, поздравляю! Вот мы и набрались достаточного количества знаний для уверенной работы с логарифмами практически на любом уровне сложности! Дальше путь только один — решать примеры! Как можно больше.) И особо рекомендую не пренебрегать зелёными советами. Они не зря даются в материале.) Их надо помнить и им надо следовать.) И тогда не логарифмы будут командовать вами, а вы — логарифмами.)
Источник