Как избавится от мультиколлинеарности

Способы избавления от мультиколлинеарности

Для борьбы с мультиколлинеарностью можно использовать следующие способы:

1. Ничего не делать;

2. Увеличить число наблюдений;

3. Исключить из модели переменную (переменные), имеющую высокую тесноту связи с другими независимыми переменными;

4. Преобразовать мультиколлинеарные переменные путем

§ представления их в виде линейной комбинации;

§ преобразования уравнения к виду логарифмического или к уравнению в первых разностях;

Первый прием предполагает создание новой переменной, которая является функцией мультиколлинеарных переменных и использование данной новой переменной взамен мультиколлинеарных в уравнении регрессии.

Второй – представление мультиколлинеарной переменной в виде разности: ;

5. Использовать статистические методы: главных компонент, гребневой регрессии, факторного анализа.

Алгортм Фаррара-Глобера.

С помощью данного алгоритма последовательно проверяется наличие мультиколлинеарности всего массива независимых переменных, каждой независимой переменной с остальными, а также попарная мультиколлинеарность.

В первом случае используется критерий («хи»-квадрат), во втором – -критерий Фишера и в третьем – -критерий Стьюдента. Алгоритм распадается на семь шагов.

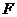
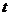
1-й шаг. Стандартизация (нормализация) данных.

Для каждого наблюдения всех независимых переменных осуществляются расчеты

. В результате получают векторы нормализованных данных , которые образуют матрицу .

2-й шаг. Нахождение корреляционной матрицы для независимых переменных.

Вычисляют или в матричном виде ,

где – матрица коэффициентов парной корреляции независимых переменных.

3-й шаг. Вычисление значения критерия для проверки гипотезы о наличии мультиколлинеарности всего массива данных.

Расчетное значение критерия получается из формулы

,

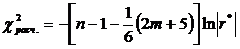
где – определитель корреляционной матрицы .

Данное значение -критерия сравнивается с табличным при числе степеней свободы и уровне значимости , где – количество независимых переменных.

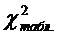
Если 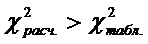, то в массиве данных имеет место мультиколлинеарность.

Следующие два шага позволяют исследовать наличие мультиколлинеарности между каждой независимой переменной и остальными независимыми переменными.

4-й шаг. Нахождение обратной матрицы

.

5-й шаг. Вычисление значений 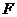-критерия Фишера для проверки гипотезы о наличии мультиколлинеарности между каждой независимой переменной и остальными независимыми переменными.

Для этого используется формула , где – диагональный элемент матрицы .

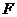
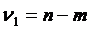
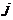
Расчетные значения -критерия сравниваются с табличными для числа степеней свободы и , и уровня значимости . Если , то -я переменная мультиколлинеарна с остальными.

Для каждой переменной можно рассчитать коэффициент детерминации

.

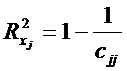
Для оценки наличия парной мультиколлинеарности производятся действия, описанные следующими двумя шагами.

6-й шаг. Расчет частных коэффициентов корреляции.

.

Частный коэффициент корреляции показывает тесноту связи между двумя переменными при условии, что остальные переменные постоянны, т.е. не меняются.

7-й шаг. Расчет значений 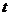-критерия Стьюдента для каждой пары независимых переменных.

Используется формула .

Расчетные значения 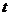-критерия сравниваются с табличным знаением при степенях свободы и уровне значимости .

Если ,то между независимыми переменными и существует мультиколлинеарность.

Дата добавления: 2018-02-18 ; просмотров: 2297 ; Мы поможем в написании вашей работы!

Источник

Мультиколлинеарность. Последствия мультиколлинеарности. Способы обнаружения мультиколлинеарности. Способы избавления от мультиколлинеарности

Ситуация, когда два фактора связаны между собой тесной линейной связью ( ), называется коллинеарностью. Коллинеарные факторы математически дублируют друг друга, поэтому один из них целесообразно исключить из рассмотрения, исходя из желаемого вида модели. Если ни одному из факторов нельзя отдать предпочтение, то в модели оставляют тот из них, который имеет больший по модулю коэффициент корреляции с результатом Y.

Когда тесной связью одновременно связаны несколько факторов, то имеет место мультиколлинеарность. Уравнение регрессии в этом случае некорректно.

Основным способом устранения мультиколлинеарности является исключение из модели одного или нескольких коллинеарных факторов. Другой способ состоит в преобразовании факторов, при котором уменьшается корреляция между ними.

Продолжения примера 2. Факторы X₁–X₂ — коллинеарные. Из них в модели целесообразно оставить фактор X₂, а фактор X₁ исключить, так как . Коллинеарными являются также и факторы X₂–X₃. Из них в модели целесообразно оставить X₃, так как . Таким образом имеет место мультиколлинеарность, и для ее устранения здесь достаточно удалить из рассмотрения фактор X₂.

Источник

Как избавится от мультиколлинеарности

Мультиколлинеарность — корреляция независимых переменных [1], которая затрудняет оценку и анализ общего результата [2]. Когда независимые переменные коррелируют друг с другом, говорят о возникновении мультиколлинеарности.

В машинном обучении (Machine Learning) мультиколлинеарность может стать причиной переобучаемости модели, что приведет к неверному результату [3]. Кроме того, избыточные коэффициенты увеличивают сложность модели машинного обучения, а значит, время ее тренировки возрастает. Еще мультиколлинеарность факторов плоха тем, что математическая модель регрессии содержит избыточные переменные, а это значит [4]:

• осложняется интерпретация параметров множественной регрессии как величин действия факторов, параметры регрессии теряют смысл и следует рассматривать другие переменные;
• оценки параметров ненадежны – получаются большие стандартные ошибки, которые меняются с изменением объема наблюдений, что делает модель регрессии непригодной для прогнозирования.

Для оценки мультиколлинеарности используется матрица парных коэффициентов корреляции, у которой необходимо вычислить определитель. При этом возможны следующие ситуации [4]:

• у совсем не коррелирующих факторов матрица парных коэффициентов корреляции единичная, у которой все элементы вне ее главной диагонали равны нулю;
• если между факторами определилась абсолютно линейная зависимость и все коэффициенты корреляции равняются единице, то определитель такой матрицы равен нулю;
• чем определитель меньше (ближе к нулю), тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии;
• чем определитель ближе к единице, тем меньше мультиколлинеарность факторов.

Две переменных коллинеарны, когда они находятся между собой в линейной зависимости, если коэффициент корреляции более 0,7. Чтобы избавиться от мультиколлинарности, необходимо исключить из модели один из факторов. Например, в эконометрике исключается фактор, который при сильной связи с результатом имеет наибольшую тесноту связи с другими переменными [4].

Источник

Мультиколлинеарность

Последствия и признаки мультиколлинеарности

Если факторные переменные связаны строгой функциональной зависимостью, то говорят о полной мультиколлинеарности. В этом случае среди столбцов матрицы факторных переменных Х имеются линейно зависимые столбцы, и, по свойству определителей матрицы, det(X T X) = 0 , т. е. матрица (X T X) вырождена, а значит, не существует обратной матрицы. Матрица (X T X) -1 используется в построении МНК-оценок. Таким образом, полная мультиколлинеарность не позволяет однозначно оценить параметры исходной модели регрессии.

К каким трудностям приводит мультиколлинеарность факторов, включенных в модель, и как они могут быть разрешены?

Мультиколлинеарность может привести к нежелательным последствиям:

1. оценки параметров становятся ненадежными. Они обнаруживают большие стандартные ошибки. С изменением объема наблюдений оценки меняются (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
2. затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;
3. становится невозможным определить изолированное влияние факторов на результативный показатель.

Вид мультиколлинеарности, при котором факторные переменные связаны некоторой стохастической зависимостью, называется частичной. Если между факторными переменными имеется высокая степень корреляции, то матрица (X T X) близка к вырожденной, т. е. det(X T X) ≈ 0.
Матрица (X T X) -1 будет плохо обусловленной, что приводит к неустойчивости МНК-оценок. Частичная мультиколлинеарность приводит к следующим последствиям:

• увеличение дисперсий оценок параметров расширяет интервальные оценки и ухудшает их точность;
• уменьшение t-статистик коэффициентов приводит к неверным выводам о значимости факторов;
• неустойчивость МНК-оценок и их дисперсий.

Точных количественных критериев для обнаружения частичной мультиколлинеарности не существует. О наличии мультиколлинеарности может свидетельствовать близость к нулю определителя матрицы (X T X). Также исследуют значения парных коэффициентов корреляции. Если же определитель матрицы межфакторной корреляции близок к единице, то мультколлинеарности нет.

Существуют различные подходы преодоления сильной межфакторной корреляции. Простейший из них – исключение из модели фактора (или факторов), в наибольшей степени ответственных за мультиколлинеарность при условии, что качество модели при этом пострадает несущественно (а именно, теоретический коэффициент детерминации -R 2 _{y(x1. xm)} снизится несущественно).

С помощью какой меры невозможно избавиться от мультиколлинеарности?
a) увеличение объема выборки;
b) исключения переменных высококоррелированных с остальными;
c) изменение спецификации модели;
d) преобразование случайной составляющей.

Парные (линейные) и частные коэффициенты корреляции

Парный коэффициент корреляции изменяется в пределах от –1 до +1. Чем ближе он по абсолютной величине к единице, тем ближе статистическая зависимость между x и y к линейной функциональной. Положительное значение коэффициента свидетельствует о том, что связь между признаками прямая (с ростом x увеличивается значение y ), отрицательное значение – связь обратная (с ростом x значение y уменьшается).
Можно дать следующую качественную интерпретацию возможных значений коэффициента корреляции: если |r| 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.
Поскольку исходные данные, по которым устанавливается взаимосвязь признаков, являются выборкой из некой генеральной совокупности, вычисленные по этим данным коэффициенты корреляции будут выборочными, т. е. они лишь оценивают связь. Необходима проверка значимости, которая отвечает на вопрос: случайны или нет полученные результаты расчетов.
Значимость парных коэффициентов корреляции проверяют по t-критерию Стьюдента. Выдвигается гипотеза о равенстве нулю генерального коэффициента корреляции: H₀: ρ = 0. Затем задаются параметры: уровень значимости α и число степеней свободы v = n-2. Используя эти параметры, по таблице критических точек распределения Стьюдента находят t_кр, а по имеющимся данным вычисляют наблюдаемое значение критерия:
, (2)
где r – парный коэффициент корреляции, рассчитанный по отобранным для исследования данным. Парный коэффициент корреляции считается значимым (гипотеза о равенстве коэффициента нулю отвергается) с доверительной вероятностью γ = 1- α, если t_Набл по модулю будет больше, чем t_крит.
Если переменные коррелируют друг с другом, то на значении коэффициента корреляции частично сказывается влияние других переменных.

Частный коэффициент корреляции характеризует тесноту линейной зависимости между результатом и соответствующим фактором при устранении влияния других факторов. Частный коэффициент корреляции оценивает тесноту связи между двумя переменными при фиксированном значении остальных факторов. Если вычисляется, например, r_yx1|x2 (частный коэффициент корреляции между y и x₁ при фиксированном влиянии x₂), это означает, что определяется количественная мера линейной зависимости между y и x₁, которая будет иметь место, если устранить влияние x₂ на эти признаки. Если исключают влияние только одного фактора, получают частный коэффициент корреляции первого порядка.
Сравнение значений парного и частного коэффициентов корреляции показывает направление воздействия фиксируемого фактора. Если частный коэффициент корреляции r_yx1|x2 получится меньше, чем соответствующий парный коэффициент r_yx1, значит, взаимосвязь признаков y и x₁ в некоторой степени обусловлена воздействием на них фиксируемой переменной x₂. И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная x₂ ослабляет своим воздействием связь y и x₁.
Частный коэффициент корреляции между двумя переменными (y и x₂) при исключении влияния одного фактора (x₁) можно вычислить по следующей формуле:
. (3)
Для других переменных формулы строятся аналогичным образом. При фиксированном x₂
;
при фиксированном x₃
.
Значимость частных коэффициентов корреляции проверяется аналогично случаю парных коэффициентов корреляции. Единственным отличием является число степеней свободы, которое следует брать равным v = n – l -2, где l – число фиксируемых факторов.
На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.

Пошаговая регрессия

На втором шаге строится уравнение регрессии с одной переменной, имеющей максимальный по абсолютной величине парный коэффициент корреляции с результативным признаком.

На третьем шаге в модель вводится новая переменная, имеющая наибольшее по абсолютной величине значение частного коэффициента корреляции с зависимой переменной при фиксированном влиянии ранее введенной переменной.
При введении в модель дополнительного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, т. е. коэффициент множественной детерминации увеличивается незначительно, то ввод нового фактора признается нецелесообразным.

Пример №1 . По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x1 (% от стоимости фондов на конец года) и от ввода в действие новых основных фондов x2 (%).

Y	X1	X2
6	10	3,5
6	12	3,6
7	15	3,9
7	17	4,1
7	18	4,2
8	19	4,5
8	19	5,3
9	20	5,3
9	20	5,6
10	21	6
10	21	6,3
11	22	6,4
11	23	7
12	25	7,5
12	28	7,9
13	30	8,2
13	31	8,4
14	31	8,6
14	35	9,5
15	36	10

Требуется:

1. Построить корреляционное поле между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации. Выдвинуть гипотезу о тесноте и виде зависимости между показателями X1 и Y .
2. Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,9.
3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости выработки продукции на одного работника от удельного веса рабочих высокой квалификации.
4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы.
5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9.
6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих.
7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров.
8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.
9. Найти коэффициенты парной и частной корреляции. Проанализировать их.
10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
11. С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9.
12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%.
13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.

Решение проводим с помощью калькулятора. Далее приводится ход решения п.13.
Матрица парных коэффициентов корреляции R:

—	y	x1	x2
y	1	0.97	0.991
x1	0.97	1	0.977
x2	0.991	0.977	1

При наличии мультиколлинеарности определитель корреляционной матрицы близок к нулю. Для нашего примера: det = 0.00081158 , что свидетельствует о наличии сильной мультиколлинеарности.
Для отбора наиболее значимых факторов x_i учитываются следующие условия:
— связь между результативным признаком и факторным должна быть выше межфакторной связи;
— связь между факторами должна быть не более 0.7. Если в матрице есть межфакторный коэффициент корреляции r_xjxi > 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.;
— при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними.
В нашем случае r_{x1 x2} имеют |r|>0.7, что говорит о мультиколлинеарности факторов и о необходимости исключения одного из них из дальнейшего анализа.
Анализ первой строки этой матрицы позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых |r_yxi| 0.3 – связь практически отсутствует; 0.3 ≤ |r| ≤ 0.7 — связь средняя; 0.7 ≤ |r| ≤ 0.9 – связь сильная; |r| > 0.9 – связь весьма сильная.
Проверим значимость полученных парных коэффициентов корреляции с помощью t-критерия Стьюдента. Коэффициенты, для которых значения t-статистики по модулю больше найденного критического значения, считаются значимыми.
Рассчитаем наблюдаемые значения t-статистики для r_yx1 по формуле:

где m = 1 — количество факторов в уравнении регрессии.

По таблице Стьюдента находим Tтабл
t_крит(n-m-1;α/2) = (18;0.025) = 2.101
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
Рассчитаем наблюдаемые значения t-статистики для r_yx2 по формуле:

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значимю
Таким образом, связь между (y и x_x1 ), (y и x_x2 ) является существенной.
Наибольшее влияние на результативный признак оказывает фактор x₂ (r = 0.99), значит, при построении модели он войдет в регрессионное уравнение первым.
Тестирование и устранение мультиколлинеарности.
Наиболее полным алгоритмом исследования мультиколлинеарности является алгоритм Фаррара-Глобера. С его помощью тестируют три вида мультиколлинеарности:
1. Всех факторов (χ 2 — хи-квадрат).
2. Каждого фактора с остальными (критерий Фишера).
3. Каждой пары факторов (критерий Стьюдента).
Проверим переменные на мультиколлинеарность методом Фаррара-Глоубера по первому виду статистических критериев (критерий «хи-квадрат»).
Формула для расчета значения статистики Фаррара-Глоубера:
χ 2 = -[n-1-(2m+5)/6]ln(det[R])
где m = 2 — количество факторов, n = 20 — количество наблюдений, det[R] — определитель матрицы парных коэффициентов корреляции R.
Сравниваем его с табличным значением при v = m/2(m-1) = 1 степенях свободы и уровне значимости α. Если χ 2 > χ_табл 2 , то в векторе факторов есть присутствует мультиколлинеарность.
χ_табл 2 (1;0.05) = 3.84146
Проверим переменные на мультиколлинеарность по второму виду статистических критериев (критерий Фишера).
Определяем обратную матрицу D = R -1 :

D =	55,365 -2,256 -52,656 -2,256 22,386 -19,642 -52,656 -19,642 72,373

Вычисляем F-критерии Фишера:

где d_kk — диагональные элементы матрицы.
Рассчитанные значения критериев сравниваются с табличными при v₁=n-m и v₂=m-1 степенях свободы и уровне значимости α. Если F_k > F_Табл, то k-я переменная мультиколлинеарна с другими.
v₁=20-2 = 18; v₂=2-1 = 1. F_Табл(18;1) = 248

Поскольку F₁ > F_табл, то переменная y мультиколлинеарна с другими.

Поскольку F₂ > F_табл, то переменная x₁ мультиколлинеарна с другими.

Поскольку F₃ > F_табл, то переменная x₂ мультиколлинеарна с другими.

Проверим переменные на мультиколлинеарность по третьему виду статистических критериев (критерий Стьюдента). Для этого найдем частные коэффициенты корреляции.
Частные коэффициенты корреляции.
Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и x_i) при условии, что влияние на них остальных факторов (x_j) устранено.
На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.


Теснота связи низкая.
Определим значимость коэффициента корреляции r_{yx1 /x2} .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:

где k = 1 — число фиксируемых факторов.

По таблице Стьюдента находим Tтабл
t_крит(n-k-2;α/2) = (17;0.025) = 2.11
Поскольку t_набл t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
Как видим, связь y и x₂ при условии, что x₁ войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x₂ остается нецелесообразным.
Можно сделать вывод, что при построении регрессионного уравнения следует отобрать факторы x₁ , x₂.

Источник