Как избавиться от мультиколлинеарности

Мультиколлинеарность. Последствия мультиколлинеарности. Способы обнаружения мультиколлинеарности. Способы избавления от мультиколлинеарности

Ситуация, когда два фактора связаны между собой тесной линейной связью ( ), называется коллинеарностью. Коллинеарные факторы математически дублируют друг друга, поэтому один из них целесообразно исключить из рассмотрения, исходя из желаемого вида модели. Если ни одному из факторов нельзя отдать предпочтение, то в модели оставляют тот из них, который имеет больший по модулю коэффициент корреляции с результатом Y.

Когда тесной связью одновременно связаны несколько факторов, то имеет место мультиколлинеарность. Уравнение регрессии в этом случае некорректно.

Основным способом устранения мультиколлинеарности является исключение из модели одного или нескольких коллинеарных факторов. Другой способ состоит в преобразовании факторов, при котором уменьшается корреляция между ними.

Продолжения примера 2. Факторы X₁–X₂ — коллинеарные. Из них в модели целесообразно оставить фактор X₂, а фактор X₁ исключить, так как . Коллинеарными являются также и факторы X₂–X₃. Из них в модели целесообразно оставить X₃, так как . Таким образом имеет место мультиколлинеарность, и для ее устранения здесь достаточно удалить из рассмотрения фактор X₂.

Источник

Способы избавления от мультиколлинеарности

Для борьбы с мультиколлинеарностью можно использовать следующие способы:

1. Ничего не делать;

2. Увеличить число наблюдений;

3. Исключить из модели переменную (переменные), имеющую высокую тесноту связи с другими независимыми переменными;

4. Преобразовать мультиколлинеарные переменные путем

§ представления их в виде линейной комбинации;

§ преобразования уравнения к виду логарифмического или к уравнению в первых разностях;

Первый прием предполагает создание новой переменной, которая является функцией мультиколлинеарных переменных и использование данной новой переменной взамен мультиколлинеарных в уравнении регрессии.

Второй – представление мультиколлинеарной переменной в виде разности: ;

5. Использовать статистические методы: главных компонент, гребневой регрессии, факторного анализа.

Алгортм Фаррара-Глобера.

С помощью данного алгоритма последовательно проверяется наличие мультиколлинеарности всего массива независимых переменных, каждой независимой переменной с остальными, а также попарная мультиколлинеарность.

В первом случае используется критерий («хи»-квадрат), во втором – -критерий Фишера и в третьем – -критерий Стьюдента. Алгоритм распадается на семь шагов.

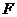
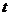
1-й шаг. Стандартизация (нормализация) данных.

Для каждого наблюдения всех независимых переменных осуществляются расчеты

. В результате получают векторы нормализованных данных , которые образуют матрицу .

2-й шаг. Нахождение корреляционной матрицы для независимых переменных.

Вычисляют или в матричном виде ,

где – матрица коэффициентов парной корреляции независимых переменных.

3-й шаг. Вычисление значения критерия для проверки гипотезы о наличии мультиколлинеарности всего массива данных.

Расчетное значение критерия получается из формулы

,

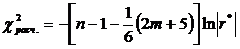
где – определитель корреляционной матрицы .

Данное значение -критерия сравнивается с табличным при числе степеней свободы и уровне значимости , где – количество независимых переменных.

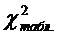
Если 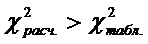, то в массиве данных имеет место мультиколлинеарность.

Следующие два шага позволяют исследовать наличие мультиколлинеарности между каждой независимой переменной и остальными независимыми переменными.

4-й шаг. Нахождение обратной матрицы

.

5-й шаг. Вычисление значений 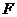-критерия Фишера для проверки гипотезы о наличии мультиколлинеарности между каждой независимой переменной и остальными независимыми переменными.

Для этого используется формула , где – диагональный элемент матрицы .

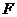
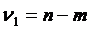
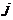
Расчетные значения -критерия сравниваются с табличными для числа степеней свободы и , и уровня значимости . Если , то -я переменная мультиколлинеарна с остальными.

Для каждой переменной можно рассчитать коэффициент детерминации

.

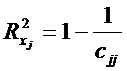
Для оценки наличия парной мультиколлинеарности производятся действия, описанные следующими двумя шагами.

6-й шаг. Расчет частных коэффициентов корреляции.

.

Частный коэффициент корреляции показывает тесноту связи между двумя переменными при условии, что остальные переменные постоянны, т.е. не меняются.

7-й шаг. Расчет значений 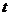-критерия Стьюдента для каждой пары независимых переменных.

Используется формула .

Расчетные значения 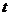-критерия сравниваются с табличным знаением при степенях свободы и уровне значимости .

Если ,то между независимыми переменными и существует мультиколлинеарность.

Дата добавления: 2018-02-18 ; просмотров: 2298 ; Мы поможем в написании вашей работы!

Источник

§ 3. Методы устранения мультиколлинеарности

Отметим, что в ряде случаев мультиколлинеарность не является таким уж серьезным «злом», чтобы прилагать существенные усилия по ее выявлению и устранению. В основном, все зависит от целей исследования.

Если основная задача модели — прогноз будущих значений зависимой переменной, то при достаточно большом коэффициенте детерминации R2(gt; 0,9) наличие мультиколлинеарности обычно не сказывается на прогнозных качествах модели (если в будущем между коррелированными переменными будут сохраняться те же отношения, что и ранее).

Если необходимо определить степень влияния каждой из объясняющих переменных на зависимую переменную, то мультиколлинеарность, приводящая к увеличению стандартных ошибок, скорее всего, исказит истинные зависимости между переменными. В этой ситуации мультиколлинеарность является серьезной проблемой.

Единого метода устранения мультиколлинеарности, годного в любом случае, не существует. Это связано с тем, что причины и последствия мультиколлинеарности неоднозначны и во многом зависят от результатов выборки.

Исключение переменной(ых) из модели

Простейшим методом устранения мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных. При применении данного метода необходима определенная осмотрительность. В данной ситуации возможны ошибки спецификации, поэтому в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока мультиколлинеарность не станет серьезной проблемой.

Получение дополнительных данных или новой выборки

Поскольку мультиколлинеарность напрямую зависит от выборки, то, возможно, при другой выборке мультиколлинеарности не будет либо она не будет столь серьезной. Иногда для уменьшения мультиколлинеарности достаточно увеличить объем выборки. Например, при использовании ежегодных данных можно перейти к поквартальным данным.

Изменение спецификации модели

В ряде случаев проблема мультиколлинеарности может быть решена путем изменения спецификации модели: либо изменяется форма модели, либо добавляются объясняющие переменные, не учтенные в первоначальной модели, но существенно влияющие на зависимую переменную. Если данный метод имеет основания, то его использование уменьшает сумму квадратов отклонений, тем самым сокращая стандартную ошибку регрессии. Это приводит к уменьшению стандартных ошибок коэффициентов.

Использование предварительной информации о некоторых параметрах

Иногда при построении модели множественной регрессии можно воспользоваться предварительной информацией, в частности известными значениями некоторых коэффициентов регрессии.

Вполне вероятно, что значения коэффициентов, рассчитанные для каких-либо предварительных (обычно более простых) моделей либо для аналогичной модели по ранее полученной выборке, могут быть использованы для разрабатываемой в данный момент модели.

Отбор наиболее существенных объясняющих переменных. Процедура последовательного присоединения элементов

Переход к меньшему числу объясняющих переменных может уменьшить дублирование информации, доставляемой сильно взаимозависимыми признаками. Именно с этим мы сталкиваемся в случае мультиколлинеарности объясняющих переменных.

корреляции между зависимой переменной Y и набором объясняющих переменных X 1,X 2. Xm.

регрессии Y = b0 + KX1 + b2X2+. + bmXm. Пусть amp; = R-1 — матрица, обратная к матрице R :

Тогда квадрат коэффициента Ry.X = Rr(xi,x2. x ) может быть вычислен по формуле:

Подправленная на несмещенность оценка R*2.X коэффициента детерминации R2y.X имеет вид:

(Если поформуле (6.7) получают отрицательное число, то полагают

Нижняя доверительная граница для

На практике, при решении вопроса о том, какие объясняющие переменные следует включать в модель, часто используют процедуру последовательного присоединения элементов.

й шаг (k = 1). Выбирается наиболее информативная объясняющая переменная, которая максимизирует величину

совпадает с квадратом обычного

парного коэффициента корреляции

тогда наиболее информативной будет переменная xp. Затем рассчитывают подправленный на несмещенность коэффициент

(при m = 1) и его нижнюю доверительную границу R2min (1) .

й шаг jk = 2) . Среди всевозможных пар объясняющих переменных jxp,xj),j = 1. m,j Ф p выбирается та, которая максимизирует величину

более информативной будет пара jxp,xq). Затемрассчитывают подправленный на несмещенность коэффициент(при m = 2)

и его нижнюю доверительную границу R2min (2) .

Процедуру продолжают до тех пор, когда на шаге (к +1) выполнится условие:

Тогда в модель включают наиболее информативные переменные, полученные на первых к шагах. Отметим, что в расчетах используют формулы (6.7) и (6.8), в которых вместо т берут соответствующее значение номера шага к.

На самом деле этот метод не гарантирует, что мы избавимся от мультиколлинеарности.

Используют и другие методы устранения мультиколлинеарности.

Пример 6.1. Имеются следующие условные данные (табл. 6.1):

Источник