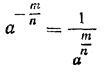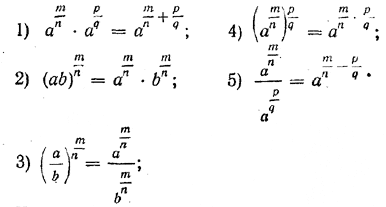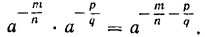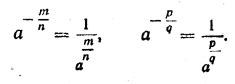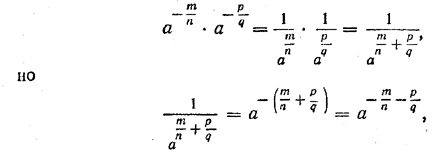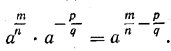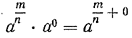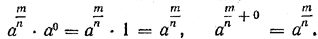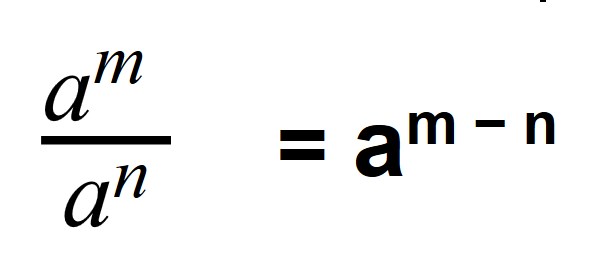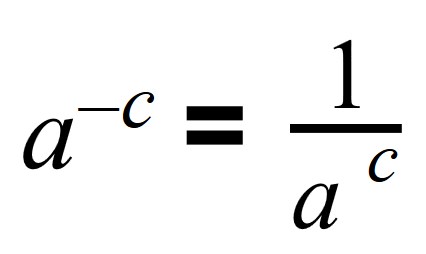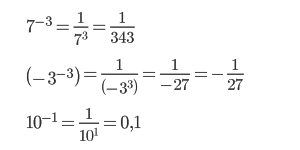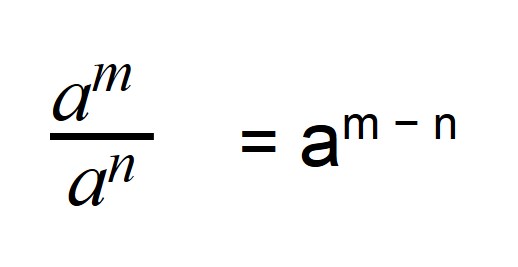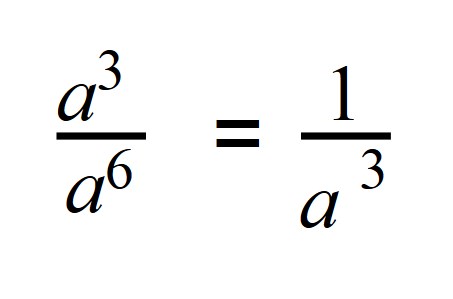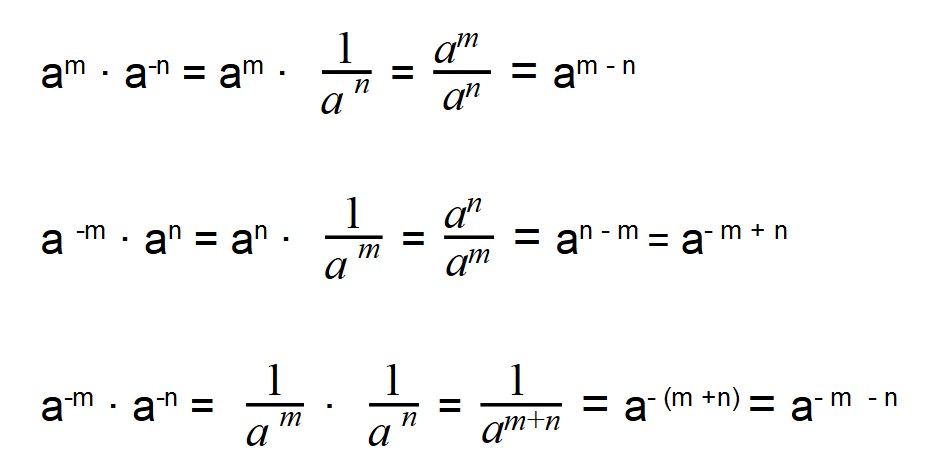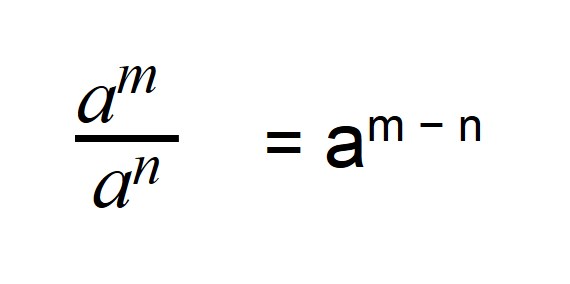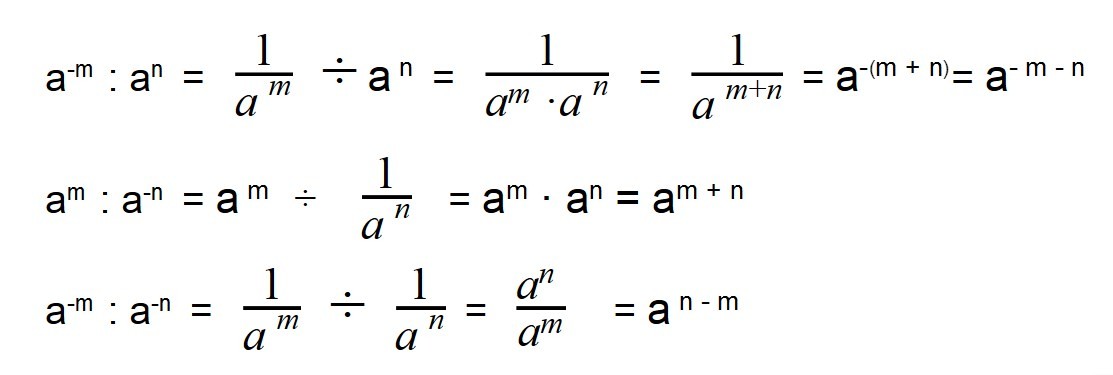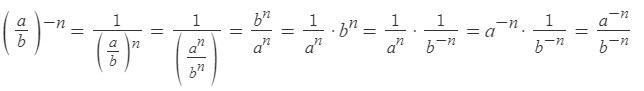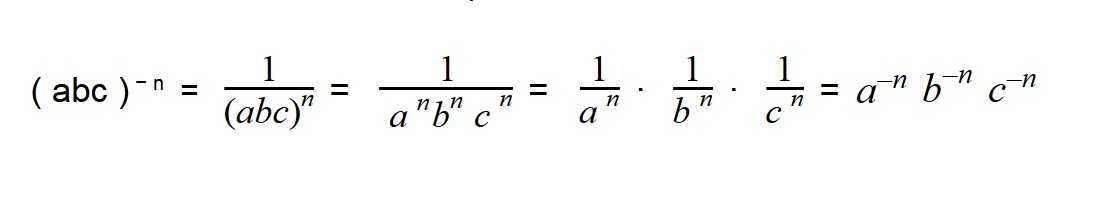- Отрицательная дробная степень числа
- Как возвести число в отрицательную дробную степень
- Считаем отрицательную дробную степень числа формула
- Разберем формулу число в отрицательной дробной степени
- Пример подсчета : «число в отрицательной дробной степени на калькуляторе»
- Как избавиться от отрицательной дробной степени
- Отрицательная степень
- Как возвести число в отрицательную степень
- Как найти 10 в минус 1 степени
- Как возвести в отрицательную степень дробь
- Как возвести отрицательное число в отрицательную степень
- Как возвести отрицательную дробь в отрицательную степень
- Свойства отрицательной степени
- Примеры решений заданий с отрицательной степенью
- Колягин 9 класс. Задание № 1
- Колягин 9 класс. Задание № 5
- Отрицательная степень
- Что такое степень числа
- Таблица степеней
- Свойства степеней
- Свойство 1: произведение степеней
- Свойство 2: частное степеней
- Свойство 3: возведение степени в квадрат
- Свойство 4: степень произведения
- Свойство 5: степень частного
- Степень с показателем 0
- Степень с отрицательным показателем
- Действия с отрицательными степенями
- Умножение отрицательных степеней
- Деление отрицательных степеней
- Возведение дроби в отрицательную степень
- Возведение произведения в отрицательную степень
Отрицательная дробная степень числа
Как посчитать отрицательную дробную степень числа на калькуляторе разберем пример!? + Разберем формулу «число в отрицательной дробной степени«
Сегодня этим и займемся!
Как возвести число в отрицательную дробную степень
Считаем отрицательную дробную степень числа формула
Чем отличается положительная дробная степень числа от отрицательной дробной степени числа!?
Тем, что после того, как вы посчитаете дробную степень числа, нужно единицу разделить на получившийся результат! Элементарно!

Разберем формулу число в отрицательной дробной степени
Возьмем ранее разобранный вариант на странице
И добавим минус, что и будет отрицательной дробной степенью числа
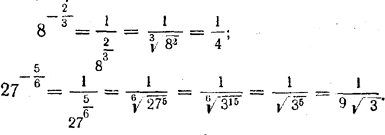
8 -1/3 = 1/ 3 √8 = 1/2 = 0.5
Пример подсчета : «число в отрицательной дробной степени на калькуляторе»
В этом пункте разберем, как можно посчитать отрицательную дробную степень числа на калькуляторе, но вначале напишем тот алгоритм, который рассматривали выше, и унас получится:
125 -1/3 = 1/ 3 √125 = 1/25 = 0.5
Чтобы проиллюстрировать работу калькулятора с отрицательной дробной степенью — на нам понадобится пример, давайте потренируемся на числе 125 и попробуем взять степень минус одна третья:
Набираем число 125 и нажимаем число степени
Теперь нам нужно набрать отрицательную степень. Набираем одну третью и ставим знак минус – нажимаем равно!
Результат возведения числа в отрицательную степень.
Источник
Как избавиться от отрицательной дробной степени
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,
СТЕПЕННАЯ ФУНКЦИЯ IV
§ 86. Степень положительного числа с отрицательным дробным показателем
Подобно тому как в § 71 мы определили степень а — п числа а с отрицательным целым показателем — п, можно определить и степень 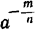
Пусть а— произвольное положительное число, а т и п — натуральные числа. Тогда по определению
Степень положительного числа с отрицательным дробным, показателем равна единице, деленной на степень того же числа с показателем, противоположным показателю данной степени.
Теперь мы знаем, что представляет собой степень положительного числа с любым рациональным показателем.
Степени с рациональными показателями обладают следующими основными свойствами:
Частично эти свойства были доказаны нами в предыдущих параграфах, но лишь для положительных показателей. Теперь же мы можем доказать их для произвольных рациональных показателей.
Докажем, например, свойство 1.
Для положительных показателей m /n и p /q доказательство было дано в предыдущем параграфе. Поэтому нам нужно рассмотреть следующие случаи:
1) оба показателя отрицательны;
2) один из показателей отрицательный, а другой — положительный;
3) хотя бы один из показателей равен нулю.
Пусть т, п, р и q — натуральные числа. Покажем, что
Действительно, по определению степени с отрицательным показателем
откуда и вытекает требуемое соотношение.
Мы рассмотрели случай, когда показатели каждой из двух степеней отрицательны. Теперь рассмотрим случай, когда один из них положителен, а другой отрицателен. Докажем, например, что
Здесь мы используем определение а 0 = 1. Таким образом,
Нам осталось рассмотреть случай, когда из двух степеней с одинаковыми основаниями хотя бы одна имеет нулевой показатель.. Докажем, например, что
Свойство 1 доказано.
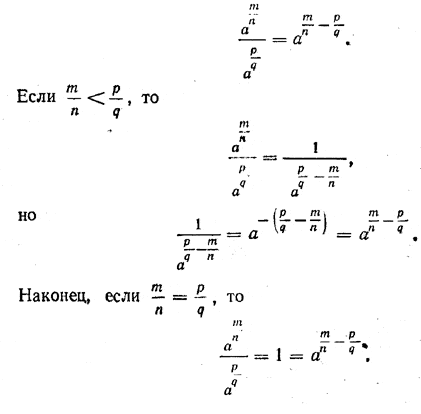
Аналогично можно доказать и все остальные свойства. Заметим, что если в предыдущем параграфе мы могли говорить о свойстве 5 лишь при m /n > p /q, то теперь, используя определения степени положительного числа с нулевым и отрицательным дробным показателем, мы можем доказать его и для случая, когда m /n p /q
Источник
Отрицательная степень
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.
Как возвести число в отрицательную степень
Чтобы возвести число в отрицательную степень нужно:
- «перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
- заменить отрицательную степень на положительную ;
- возвести число в положительную степень.
Общая формула возведения в отрицательную степень выглядит следующим образом.
a −n =
| 1 |
| a n |
,где a ≠ 0, n ∈ z ( n принадлежит целым числам).
Примеры возведения в отрицательную степень.
- 6 −2 =
1 6 2 =
1 36 - (−3) −3 =
1 (−3) 3 =
1 −27 = −
1 27 - 0,2 −2 =
1 0,2 2 =
1 0,04
Любое число в нулевой степени — единица.
Примеры возведения в нулевую степень.
- (
2 3 ) 0 = 1
- (−5) 0 = 1
Как найти 10 в минус 1 степени
В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».
Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «
| 1 |
| 10 |
» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».
Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
10 −1 =
| 1 |
| 10 1 |
=
| 1 |
| 10 |
= 0,1
По такому же принципу можно найти « 10 » в минус второй, третьей и т.д.
Для упрощения перевода « 10 » в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один ».
Проверим правило выше для « 10 −2 ».
Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».
Рассмотрим « 10 −1 ».
Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».
То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.
Как возвести в отрицательную степень дробь
Чтобы возвести дробь в отрицательную степень нужно:
- «перевернуть» дробь;
- заменить отрицательную степень на положительную ;
- возвести дробь в положительную степень.
Пример. Требуется возвести в отрицательную степень дробь.
Перевернем дробь «
| 10 |
| 3 |
» и заменим отрицательную степень « −3 » на положительную « 3 ».
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.
(
| 10 |
| 3 |
) −3 = (
| 3 |
| 10 |
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
(
| 10 |
| 3 |
) −3 = (
| 3 |
| 10 |
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
= 0,027
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.
Отрицательное число, возведённое в чётную степень, — число положительное .
Отрицательное число, возведённое в нечётную степень, — число отрицательное .
Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».
Так как степень « 2 » — четная , значит, результат возведения в степень будет положительный . Поэтому убираем знак минуса при раскрытии скобок.
Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».
(−5) −2 = (−
| 1 |
| 5 |
) 2 =
| 1 2 |
| 5 2 |
=
| 1 |
| 25 |
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Отрицательная дробь, возведённая в чётную степень, — дробь положительная .
Отрицательная дробь, возведённая в нечётную степень, — дробь отрицательная .
Разберемся на примере. Задание: возвести отрицательную дробь « (−
| 2 |
| 3 |
) » в « −3 » степень.
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».
Теперь определим конечный знак результата возведения в « 3 » степень.
Степень « 3 » — нечетная , значит, по правилу возведения отрицательного числа в степень дробь останется отрицательной .
Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.
(−
| 2 |
| 3 |
) −3 = (−
| 3 |
| 2 |
) 3 = −
| 3 3 |
| 2 3 |
= −
| 27 |
| 8 |
Для окончательного ответа выделим целую часть из дроби.
(−
| 2 |
| 3 |
) −3 = (−
| 3 |
| 2 |
) 3 = −
| 3 3 |
| 2 3 |
= −
| 27 |
| 8 |
= − 3
| 3 |
| 8 |
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
Правило возведения отрицательного числа в степень гласит: если степень четная , значит, результат возведения будет положительным .
(−
| 9 |
| 11 |
) −2 = (−
| 11 |
| 9 |
) 2 =
| 11 2 |
| 9 2 |
=
| 121 |
| 81 |
= 1
| 40 |
| 81 |
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.
Запомните!
- a m · a n = a m + n
-
a m a n = a m − n
- (a n ) m = a n · m
- (a · b) n = a n · b n
Примеры решений заданий с отрицательной
степенью
Колягин 9 класс. Задание № 1
Представить в виде степени.
2) a 6 · b 6 = (ab) 6
Колягин 9 класс. Задание № 5
Записать в виде степени с отрицательным числом.
Источник
Отрицательная степень
О чем эта статья:
7 класс, 8 класс
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
- a — основание степени,
- n — показатель степени.
Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 3 = 2 · 2 · 2, где:
- 2 — основание степени,
- 3 — показатель степени.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Свойства степеней
Степень с натуральным показателем в математике имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
a m · a n = a m + n
- a — основание степени.
- m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
- a — любое число, не равное нулю.
- m, n — любые натуральные числа, такие, что m > n
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
- a — основание степени (не равное нулю).
- m, n — показатели степени, натуральное число.
Свойство 4: степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b) n = a n · b n
- a, b — основание степени (не равное нулю).
- n — показатели степени, натуральное число.
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень сначала делимое, потом делитель, и первый результат разделить на второй.
(a : b) n = a n : b n
- a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0.
- n — показатель степени, натуральное число.
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0; 0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
К примеру, 4 в минус 2 степени — это 1/4 2 , 2 в минус 3 степени — это 1/2 3 , 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 или 0,1.
Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины. Например, одну миллиардную долю (0, 000 000 001) можно записать как 10 в минус 9 степени (10 -9 ). В школьной программе такие величины — редкость: чаще всего используют 10 в минус 1 степени или 2 в минус 1 степени.
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
a 3 : a 6 =a 3 — 6 = a -3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
a m · a n = a m + n
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Источник