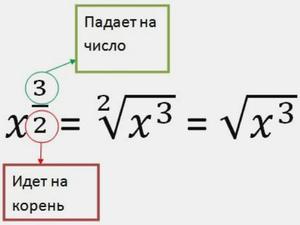
- Отрицательная степень числа
- Степень с отрицательным показателем
- Действия над степенями с отрицательными показателями
- Отрицательная степень
- Как возвести число в отрицательную степень
- Как найти 10 в минус 1 степени
- Как возвести в отрицательную степень дробь
- Как возвести отрицательное число в отрицательную степень
- Как возвести отрицательную дробь в отрицательную степень
- Свойства отрицательной степени
- Примеры решений заданий с отрицательной степенью
- Колягин 9 класс. Задание № 1
- Колягин 9 класс. Задание № 5
- Отрицательная степень числа: правила возведения и примеры
- Определение понятия
- Возведение в отрицательную степень
- Как возвести число в натуральную степeнь
- Возведение в иррациональную стeпeнь
- Как возвести чиcло в целую степень
- Видео
Отрицательная степень числа
Степень с отрицательным показателем
Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.
| d -c = | 1 | ; 7 -5 = | 1 | ; a -5 = | 1 | . |
| d c | 7 5 | a 5 |
Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
| a 5 | = | 1 | . |
| a 8 | a 3 |
| a -3 = | 1 | . |
| a 3 |
Пример 1. Замените дробь степенью с отрицательным показателем:
| 1 | . |
| x 2 |
| 1 | = x -2 . |
| x 2 |
Пример 2. Представьте в виде степени с отрицательным показателем:
| 1 | . |
| (m + n) 2 |
| 1 | = (m + n) -2 . |
| (m + n) 2 |
Действия над степенями с отрицательными показателями
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:
Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются:
Источник
Отрицательная степень
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.
Как возвести число в отрицательную степень
Чтобы возвести число в отрицательную степень нужно:
- «перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
- заменить отрицательную степень на положительную ;
- возвести число в положительную степень.
Общая формула возведения в отрицательную степень выглядит следующим образом.
a −n =
| 1 |
| a n |
,где a ≠ 0, n ∈ z ( n принадлежит целым числам).
Примеры возведения в отрицательную степень.
- 6 −2 =
1 6 2 =
1 36 - (−3) −3 =
1 (−3) 3 =
1 −27 = −
1 27 - 0,2 −2 =
1 0,2 2 =
1 0,04
Любое число в нулевой степени — единица.
Примеры возведения в нулевую степень.
- (
2 3 ) 0 = 1
- (−5) 0 = 1
Как найти 10 в минус 1 степени
В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».
Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «
| 1 |
| 10 |
» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».
Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
10 −1 =
| 1 |
| 10 1 |
=
| 1 |
| 10 |
= 0,1
По такому же принципу можно найти « 10 » в минус второй, третьей и т.д.
Для упрощения перевода « 10 » в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один ».
Проверим правило выше для « 10 −2 ».
Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».
Рассмотрим « 10 −1 ».
Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».
То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.
Как возвести в отрицательную степень дробь
Чтобы возвести дробь в отрицательную степень нужно:
- «перевернуть» дробь;
- заменить отрицательную степень на положительную ;
- возвести дробь в положительную степень.
Пример. Требуется возвести в отрицательную степень дробь.
Перевернем дробь «
| 10 |
| 3 |
» и заменим отрицательную степень « −3 » на положительную « 3 ».
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.
(
| 10 |
| 3 |
) −3 = (
| 3 |
| 10 |
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
(
| 10 |
| 3 |
) −3 = (
| 3 |
| 10 |
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
= 0,027
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.
Отрицательное число, возведённое в чётную степень, — число положительное .
Отрицательное число, возведённое в нечётную степень, — число отрицательное .
Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».
Так как степень « 2 » — четная , значит, результат возведения в степень будет положительный . Поэтому убираем знак минуса при раскрытии скобок.
Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».
(−5) −2 = (−
| 1 |
| 5 |
) 2 =
| 1 2 |
| 5 2 |
=
| 1 |
| 25 |
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Отрицательная дробь, возведённая в чётную степень, — дробь положительная .
Отрицательная дробь, возведённая в нечётную степень, — дробь отрицательная .
Разберемся на примере. Задание: возвести отрицательную дробь « (−
| 2 |
| 3 |
) » в « −3 » степень.
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».
Теперь определим конечный знак результата возведения в « 3 » степень.
Степень « 3 » — нечетная , значит, по правилу возведения отрицательного числа в степень дробь останется отрицательной .
Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.
(−
| 2 |
| 3 |
) −3 = (−
| 3 |
| 2 |
) 3 = −
| 3 3 |
| 2 3 |
= −
| 27 |
| 8 |
Для окончательного ответа выделим целую часть из дроби.
(−
| 2 |
| 3 |
) −3 = (−
| 3 |
| 2 |
) 3 = −
| 3 3 |
| 2 3 |
= −
| 27 |
| 8 |
= − 3
| 3 |
| 8 |
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
Правило возведения отрицательного числа в степень гласит: если степень четная , значит, результат возведения будет положительным .
(−
| 9 |
| 11 |
) −2 = (−
| 11 |
| 9 |
) 2 =
| 11 2 |
| 9 2 |
=
| 121 |
| 81 |
= 1
| 40 |
| 81 |
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.
Запомните!
- a m · a n = a m + n
-
a m a n = a m − n
- (a n ) m = a n · m
- (a · b) n = a n · b n
Примеры решений заданий с отрицательной
степенью
Колягин 9 класс. Задание № 1
Представить в виде степени.
2) a 6 · b 6 = (ab) 6
Колягин 9 класс. Задание № 5
Записать в виде степени с отрицательным числом.
Источник
Отрицательная степень числа: правила возведения и примеры
В одной из предыдущих статей мы уже упоминали о степени числа. Сегодня мы постараемся сориентироваться в процессе нахождения ее значения. Научно говоря, мы будем выяснять, как правильно возводить в степень. Мы разберемся, как производится этот процесс, одновременно затронем все вероятные показатели степени: натуральный, иррациональный, рациональный, целый.
Итак, давайте подробно рассмотрим решения примеров и выясним, что значит:
- Определение понятия.
- Возведение в отрицательную ст.
- Целый показатель.
- Возведение числа в иррациональную степень.
Определение понятия
Вот точно отражающее смысл определение: «Возведением в степень называют определение значения степени числа».
Соответственно, возведение числа a в ст. r и процесс нахождения значения степени a с показателем r — это идентичные понятия. К примеру, если стоит задача вычислить значение степени (0,6)6″, то ее можно упростить до выражения «Возвести число 0,6 в степень 6».
После этого можно приступать напрямую к правилам возведения.
Возведение в отрицательную степень
Минусовая степень обозначает, что число множат на него самого такое количество раз, какое значится в ст., а после этого единицу делят на вычисленный результат.
Для наглядности следует обратить внимание на такую цепочку выражений:
110=0,1=1* 10 в минус 1 ст.,
1100=0,01=1*10 в минус 2 степ.,
11000=0,0001=1*10 в минус 3 ст.,
110000=0,00001=1*10 в минус 4 степeни.
Благодаря данным примерам можно четко просмотреть возможность моментально вычислить 10 в любой минусовой степени. Для этой цели достаточно банально сдвигать десятичную составляющую:
- 10 в -1 степeни — перед единицей 1 ноль;
- в -3 — три нуля перед единицей;
- в -9 — это 9 нулей и проч.
Так же легко понять по данной схеме, сколько будет составлять 10 в минус 5 ст. —
Как возвести число в натуральную степeнь
Вспоминая определение, учитываем, что натуральное число a в ст. n равняется произведению из n множителей, при этом каждый из них равняется a. Проиллюстрируем: (а*а*…а)n, где n — это количество чисел, которые умножаются. Соответственно, чтобы a возвести в n, необходимо рассчитать произведение следующего вида: а*а*…а разделить на n раз.
Отсюда становится очевидно, что возведение в натуральную ст. опирается на умение осуществлять умножение (этот материал освещен в разделе про умножение действительных чисел). Давайте рассмотрим задачу:
Возведите -2 в 4-ю ст.
Мы имеем дело с натуральным показателем. Соответственно, ход решения будет следующим: (-2) в cт. 4 = (-2)*(-2)*(-2)*(-2). Теперь осталось только осуществить умножение целых численностей:(-2)*(-2)*(-2)*(-2). Получаем 16.
Ответ на задачу:
Пример:
Вычислите значение: три целых две седьмых в квадрате.
Данный пример равняется следующему произведению: три целых две седьмых умножить на три целых две седьмых. Припомнив, как осуществляется умножение смешанных чисел, завершаем возведение:
- 3 целых 2 седьмых умножить на самих себя;
- равно 23 седьмых умножить на 23 седьмых;
- равно 529 сорок девятых;
- сокращаем и получаем 10 тридцать девять сорок девятых.
Возведение в иррациональную стeпeнь
Касаемо вопроса возведения в иррациональный показатель, следует отметить что расчеты начинают проводить после завершения предварительного округления основы степени до какого-либо разряда, который позволил бы получить величину с заданной точностью. К примеру, нам необходимо возвести число П (пи) в квадрат.
Начинаем с того, что округляем П до сотых и получаем:
П в квадрате = (3,14)2=9,8596. Однако если сократить П до десятитысячных, получим П=3,14159. Тогда возведение в квадрат получает совсем другое чиcло: 9,8695877281.
Здесь следует отметить, что во многих задачах нет надобности возводить иррациональные числа в cтeпeнь. Как правило, ответ вписывается или в виде, собственно, степени, к примеру, корень из 6 в степени 3, либо, если позволит выражение, проводится его преобразование: корень из 5 в 7 cтепeни = 125 корень из 5.
Как возвести чиcло в целую степень
Эту алгебраическую манипуляцию уместно принимать во внимание для следующих случаев:
- для целых чисел;
- для нулевого показателя;
- для целого положительного показателя.
Поскольку практически все целые положительные числа совпадают с массой чисел натуральных, то постановка в положительную целую степень — это тот же процесс, что и постановка в ст. натуральную. Данный процесс мы описали в предшествующем пункте.
Теперь поговорим о вычислении ст. нулевой. Мы уже выяснили выше, что нулевую степень числа a можно определить для любого отличного от нуля a (действительного), при этом a в ст. 0 будет равно 1.
Соответственно, возведение какого угодно действительного числа в нулевую ст. будет давать единицу.
К примеру, 10 в ст.0=1, (-3,65)0=1, а 0 в ст. 0 нельзя определить.
Для того чтобы завершить возведение в целую степень, остается определиться с вариантами целых отрицательных значений. Мы помним, что ст. от a с целым показателем -z будет определяться как дробь. В знаменателе дроби располагается ст. с целым положительным значением, значение которой мы уже научились находить. Теперь остается лишь рассмотреть пример возведения.
Пример:
Вычислить значение числа 2 в кубе с целым отрицательным показателем.
Согласно определению стeпeни с отрицательным показателем обозначаем: два в минус 3 ст. равняется один к двум в третьей cтепeни.
Знаменатель рассчитывается просто: два в кубе;
Ответ: два в минус 3-й ст. = одна восьмая.
Видео
Из этого видео вы узнаете, что делать, если степень с отрицательным показателем.
Источник