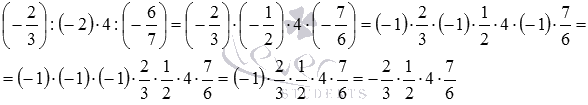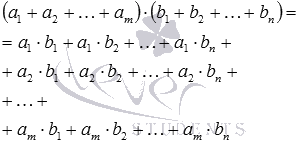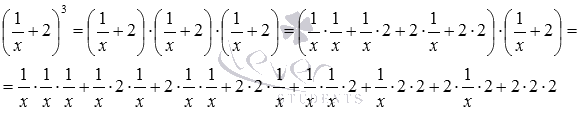Как избавится от скобок

Раскрытие скобок: правила и примеры

Раскрытие скобок и правила применения — это одна из основных тем математике, на базе которой решаются многие задания во всех последующих классах. Поэтому правила раскрытия скобок необходимо усвоить в обязательном порядке.

Итак, основная функция скобок – задать порядок вычислений, так как в зависимости от того, в какой последовательности будут решаться примеры и выражения, зависит ответ. Раскрыть скобки означает избавиться от них, не влияя на результат . При этом существуют правила, которые применяются при раскрытии скобок.

Раскрытие скобок: правила

Правило раскрытия скобок при сложении

Если перед скобками стоит плюс, то скобки просто опускаются.
Иными словами, скобки исчезнут, а то, что было в скобках, запишется без изменений.
Например, (a−b) = a−b.

В данном правиле следует учитывать, что в математике не принято писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа 2 и 3, то запишем 2+3, а не +2+3. Значит перед скобками, которые стоят в начале выражения, стоит плюс, который не пишут.

Пример 1: 8+(5−3) = 10. Ответ: 8+5–3 = 10.
Пример 2: 6+(−1+2) = 7. Ответ: 6–1+2 = 7.
Пример 3: 8a + (3b −6a). Ответ: 8a + 3b −6a = 2a + 3b.

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то скобки опускаются, а каждое слагаемое внутри нее меняет свой знак на противоположный.
Например, −(a−b) = −a+b

Пример 1: 8–(5–3) = 6. Ответ: 8 – 5 + 3 = 6.
Пример 2: 6 − (−1 + 2) = 5. Ответ: 6 + 1 – 2 = 5.
Пример 3: 8a–(3b −6a). Ответ: 8a – 3b + 6a = 14a – 3b.
Пример 4: −(5b −2). Ответ: −5b +2.

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число внутри скобок умножается на множитель, стоящий перед скобками.
При этом умножение минуса на минус дает плюс, а умножение минуса на плюс дает минус.
Данное правило основано на распределительном законе умножения: a(b+c) = ab + ac.

Пример 1: 8×(5 − 3) = 16. Ответ: 8 ×5 − 8 ×3 = 16.
Пример 2: a×(7 +2). Ответ: a×7+a×2 = 7a + 2a = 9a.
Пример 3: 8×(3b −6a). Ответ: 8×3b – 8×6a = 24b–48a

Раскрытие скобок при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок.

Пример 1: (25−15):5. Ответ: 25:5−15:5= 2.
Пример 2: (−14a +10):2. Ответ: −14a:2 +10:2 = −7a +5.
Пример 3: (36b + 6a):6. Ответ: 36b:6 + 6a:6 = 6b + a.

Раскрытие скобок при умножении двух скобок

При умножении скобки на скобку, каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки.
Например, (c+d) × (a−b) = c×(a−b)+d×(a−b) = ca−cb+da−db

Пример. Раскрыть скобки: (2−a) × (3a−1).
Решение:
Шаг 1. Убираем первую скобку (каждое ее слагаемое умножаем на вторую скобку): 2 × (3a−1) − a × (3a−1).
Шаг 2. Раскрываем произведение скобок: (2×3a− 2×1) – (a×3a−a×1) = 2×3a− 2×1 – a×3a + a×1.
Шаг 3. Перемножаем и приводим подобные слагаемые: 6a–2–3a2+a = 7a–2–3a2

Раскрытие вложенных скобок

Иногда встречаются примеры со скобками, которые вложены в другие скобки. Чтобы решить такую задачу, нужно сначала раскрыть внутреннюю скобку (при этом остальное выражение оставить без изменений), а потом внешнюю скобку.

Пример 1. 7a + 2 × (5− (3a+b)).
Решение:
Шаг 1. Раскроем внутреннюю скобку (не трогая остальное): 7a + 2 × (5 − (3a+b)) = 7a + 2 × (5 − 3a − b).
Шаг 2. Раскроем внешнюю скобку: 7a + 2 × (5 − (3a+b)) = 7a + 2×5 − 2×3a − 2×b.
Шаг 3. Упростим выражение: 7a + 10 − 6a − 2b = a+10-2b.

Раскрытие скобок в натуральной степени

Если стоит скобка в натуральной степени (n), то чтобы раскрыть скобки, нужно найти произведение скобок, перемноженных несколько раз (n раз).

Например, в примере (a+b)2 = (a+b)×(a+b) нужно перемножить скобки (a+b) два раза, далее раскрываем скобки, где каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки.

Источник

Раскрытие скобок: правила, примеры, решения.

Одним из видов преобразования выражения является раскрытие скобок. В этой статье мы разберемся, что называют раскрытием скобок, подробно опишем правила раскрытия скобок и рассмотрим применение этих правил при решении примеров.

Навигация по странице.

Что называется раскрытием скобок?

Числовые, буквенные выражения и выражения с переменными бывают составлены с использованием скобок, которые могут указывать порядок выполнения действий, содержать отрицательное число и т.п. Бывает удобно перейти от этого выражения со скобками к тождественно равному выражению, которое уже не содержит этих скобок. К примеру, от выражения 2·(3+4) можно перейти к выражению без скобок вида 2·3+2·4 . Этот переход от выражения со скобками к тождественно равному выражению без скобок дает представление о раскрытии скобок.

В школьном курсе математики к раскрытию скобок подходят в 6 классе. На этом этапе под раскрытием скобок понимают избавление от скобок, указывающих порядок выполнения действий. А изучают раскрытие скобок при рассмотрении выражений, которые содержат:

• знаки плюс или минус перед скобками, заключающими суммы и/или разности, например, (a+7) и −(−3+2·a−12−b) ;
• произведение числа, одной или нескольких букв и суммы и/или разности в скобках, например, 3·(2−7) , (3−a+8·c)·(−b) или −2·a·(b+2·c−3·m) .

Однако ничто не мешает раскрытие скобок рассматривать немного шире. Почему бы не назвать раскрытием скобок переход от выражения, содержащего отрицательные числа в скобках, к выражению без скобок, например, переход от 5+(−3)−(−7) к 5−3+7 ? Или замена произведения выражений в скобках вида (a+b)·(c+d) на сумму a·c+a·d+b·c+b·d противоречит смыслу раскрытия скобок?

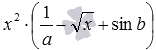
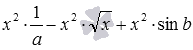
Можно пойти еще дальше. Допустим, что в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Для иллюстрации возьмем выражение , ему соответствует выражение без скобок вида .

Итак, мы под раскрытием скобок будем понимать избавление от скобок, указывающих порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

И обратим внимание еще на один момент, касающийся особенностей записи решения при раскрытии скобок. Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства. Например, выражение 3−(5−7) после раскрытия скобок принимает вид 3−5+7 , это наглядно отражает равенство 3−(5−7)=3−5+7 . При раскрытии скобок в громоздких выражениях возникает необходимость в записи промежуточных результатов, в этом случае решение удобно оформлять в виде цепочки равенств, к примеру, 5−(3−(2−1))=5−(3−2+1)=5−3+2−1 или 5−(3−(2−1))=5−3+(2−1)=5−3+2−1 .

Правила раскрытия скобок, примеры

В предыдущем пункте мы разобрались с тем, что называют раскрытием скобок. Пришло время поговорить о том, как оно выполняется. Для этого существуют правила раскрытия скобок, к обзору которых мы и приступаем.

У одиночных чисел в скобках

В выражениях можно встретить отрицательные числа в скобках, например, (−4) и 3+(−4) . Иногда можно встретить и положительные числа в скобках, к примеру, (4) и 3+(4) .

Сначала сформулируем правило раскрытия скобок, в которые заключены одиночные положительные числа: пусть a – положительное число, тогда (a) заменяется на a , +(a) заменяется на +a и −(a) заменяется на −a .

Например, число (5) запишется как 5 , выражение 3+(5) без скобок примет вид 3+5 , так как +(5) заменяется на +5 , а выражение 3+(−5) эквивалентно выражению 3−5 , так как +(−5) заменяется на −5 .

Это правило продиктовано тем, что положительные числа принято записывать без скобок, скобки в этом случае излишни.

Можно переходить к правилу раскрытия скобок, в которых содержатся одиночные отрицательные числа: +(−a) заменяется на −a , а −(−a) заменяется на +a , если же выражение начинается с отрицательного числа (−a) , записанного в скобках, то скобки, содержащие это число, просто опускаются, и вместо (−a) остается −a .

Рассмотрим примеры. Возьмем простейшее выражение, состоящее из одного отрицательного числа в скобках, например, (−5) . Его можно записать без скобок как −5 . Аналогично, в выражении (−3)+0,5 скобки можно опустить, выражение примет вид −3+0,5 . Дальше рассмотрим выражение 4+(−3) , для избавления от скобок нам нужно согласно правилу заменить +(−3) на −3 , имеем 4−3 . Наконец, выражение −(−4)−(−3) после раскрытия скобок примет вид 4+3 , так как −(−4) и −(−3) заменяется на +4 и +3 , а положительное число +4 вначале выражения можно записать без знака плюс (об этом мы упоминали при знакомстве с положительными и отрицательными числами). Для закрепления материала приведем еще один пример. Выражение (−3,7)−(−2)+4+(−9) может быть записано без скобок как −3,7+2+4−9 .

Отдельно заметим, что выражение 3·(−5) нельзя записать как 3·−5 , так как озвученное правило не говорит нам о том, на что заменяется отрицательное число в скобках со знаком умножить перед ними вида ·(−a) . О раскрытии скобок в подобных выражениях мы поговорим в следующих пунктах.

Теперь поясним, на чем базируется приведенное правило раскрытия скобок.

Первая часть правила следует из того, что разность a−b равна a+(−b) , так как в силу свойств действий с числами справедлива цепочка равенств (a+(−b))+b=a+((−b)+b)=a+0=a , которая в силу смысла вычитания доказывает, что a+(−b) есть ни что иное как разность a−b . Вторая часть правила следует из свойства противоположных чисел, которому соответствует формула −(−a)=a , а также правила вычитания отрицательного числа вида a−(−b)=a+b . Наконец, третья часть правила просто обусловлена особенностями записи отрицательных чисел, стоящих слева в выражении (о чем мы упоминали в разделе скобки для записи отрицательных чисел).

Можно столкнуться с выражениями, составленными из числа, знаков минус и нескольких пар скобок. Приведенные выше правила позволяют избавиться от скобок в них. При этом удобно раскрытие скобок проводить, последовательно продвигаясь либо от внутренних скобок к внешним, либо наоборот – от внешних к внутренним. Для примера раскроем скобки в выражении − ( − ( ( −(5) ) ) ) , для наглядности пары скобок мы изобразили разными цветами. Если раскрывать скобки, продвигаясь от внутренних к внешним, то решение будет таким: − ( − ( ( −(5) ) ) ) =− ( − ( ( −5 ) ) ) =− ( − ( −5 ) ) =− ( 5 ) =−5 . Если двигаться в обратном направлении, то соответствующая цепочка равенств будет иметь вид − ( − ( ( −(5) ) ) ) = ( ( −(5) ) ) = ( −(5) ) =−(5)=−5 .

Озвученные в этом пункте правила, можно использовать и в том случае, если под a и b понимать не только числа, а произвольные числовые или буквенные выражения, со знаком плюс впереди, которые не являются суммами или разностями (тогда −a и −b будут аналогичными выражениями, но со знаком минус впереди). Например, выражение −(−2·x)−(x 2 )+(−1/x)−(2·x·y 2 :z) после раскрытия скобок примет вид 2·x−x 2 −1/x−2·x·y 2 :z . Вот тому пояснение: −(−2·x) есть +2·x , а так как это выражение стоит вначале, то +2·x можно записать как 2·x , −(x 2 )=−x 2 , +(−1/x)=−1/x и −(2·x·y 2 :z)=−2·x·y 2 :z .

В произведениях двух чисел

Начнем с правила раскрытия скобок в произведении двух чисел.

Пусть a и b – положительные числа. Тогда произведение двух отрицательных чисел −a и −b вида (−a)·(−b) заменяется на (a·b) , а произведения двух чисел с противоположными знаками вида (−a)·b и a·(−b) заменяются на (−a·b) .

Иными словами, умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Первая часть записанного правила раскрытия скобок напрямую следует из правила умножения отрицательных чисел. Вторая его часть является следствием правила умножения чисел с разными знаками.

Аналогичное правило справедливо и для частного двух чисел, так как деление можно рассматривать как умножение на обратное число.

Переходим к примерам.

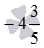
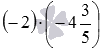
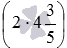
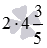
Начнем с примеров раскрытия скобок в произведениях и частных двух отрицательных чисел. Произведение двух отрицательных чисел −2 и вида можно заменить на , а окончательно раскрыть скобки можно на базе информации предыдущего пункта этой статьи, в итоге имеем . Аналогично, частное отрицательных чисел вида (−4):(−2) без скобок запишется как 4:2 .

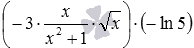
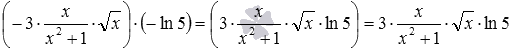
Вместо отрицательных чисел −a и −b могут быть любые выражения со знаком минус впереди, не являющиеся суммами или разностями, например, произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п. Для примера, раскроем скобки в выражении . Согласно записанному выше правилу, получаем .

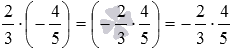
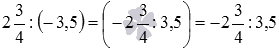
Переходим к примерам раскрытия скобок в произведениях и частных двух чисел с разными знаками. Выражение (−3)·2 по озвученному выше правилу можно записать как (−3·2) , оно после окончательного раскрытия скобок примет вид −3·2 . Аналогично . Вот еще примеры раскрытия скобок при делении чисел с разными знаками: так (−5):2=(−5:2)=−5:2 и .

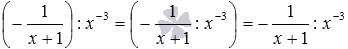
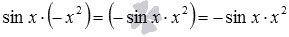
Аналогичное правило применяется при умножении и делении выражений, имеющих разные знаки. Например, и .

В произведениях трех и большего количества чисел

Теперь от произведений и частных двух чисел перейдем к произведениям и частным с бо́льшим количеством чисел. Для раскрытия скобок, содержащих отрицательные числа, в таких выражениях следует руководствоваться следующим правилом:

Если количество отрицательных чисел четно, то можно опустить скобки, заменив эти числа противоположными, после чего заключить полученное выражение в новые скобки; если же количество отрицательных чисел нечетно, то нужно опустить скобки, заменить эти числа на противоположные, поставить минус перед полученным выражением и заключить его в скобки.

Например, произведение трех чисел 5·(−3)·(−2) содержит два отрицательных числа, так как 2 – четное число, то по озвученному правилу исходное выражение можно записать как (5·3·2) , а после окончательного раскрытия скобок оно примет вид 5·3·2 . А выражение (−2,5)·(−3):(−2)·4:(−1,25):(−1) содержит пять отрицательных чисел, 5 – нечетное число, поэтому (−2,5)·(−3):(−2)·4:(−1,25):(−1)= (−2,5·3:2·4:1,25:1) , и после окончательного раскрытия скобок оно будет иметь вид −2,5·3:2·4:1,25:1 .

Дадим обоснование приведенного правила. Во-первых, такие выражения можно переписать в виде произведения, заменив деление умножением на обратное число. Дальше каждое отрицательное число можно представить в виде произведения −1 и соответствующего положительного числа, то есть, каждое отрицательное число (−a) можно заменить на (−1)·a . Переместительное свойство умножения позволяет менять множители местами, что дает возможность все множители, равные −1 , перенести в начало выражения. Наконец, произведение четного числа минус единиц равно 1 , а нечетного – равно −1 , что объясняет постановку знака минус.

Приведенное выше правило учитывает всю цепочку этих действий и значительно ускоряет процесс раскрытия скобок. Если бы мы его не использовали, то раскрытие скобок в выражении 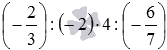выглядело бы так:

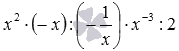
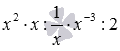
Это же правило позволяет раскрывать скобки в выражениях, представляющих собой произведения и частные выражений со знаком минус, не являющихся суммами и разностями. К примеру, выражение можно привести к выражению без скобок вида .

Раскрытие скобок, перед которыми стоит знак +

В этом пункте мы запишем правило раскрытия скобок, перед которыми стоит знак плюс, и эти скобки не умножаются или делятся на какое-либо число или выражение. О раскрытии скобок, которые умножаются на число или выражение мы поговорим в одном из следующих пунктов.

Правило раскрытия скобок, перед которыми стоит знак плюс или не стоит никакого знака, таково: скобки вместе с этим знаком опускаются, а знаки всех слагаемых в скобках сохраняются. При этом если первое слагаемое в скобках записано без знака, то перед ним нужно поставить знак плюс.

Рассмотрим примеры применения этого правила.

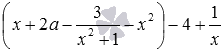
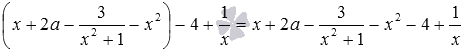
Возьмем выражение (12−3,5)−7 . Здесь скобки опускаются, знаки слагаемых в скобках сохраняются, а перед первым слагаемым ставится плюс, получаем (12−3,5)−7=+12−3,5−7 . Здесь знак плюс перед первым слагаемым можно было не ставить, так как +12−3,5−7=12−3,5−7 . Абсолютно аналогично скобки раскрываются в выражении , имеем .

Еще примеры: выражение 3+(−4+7) после раскрытия скобок примет вид 3−4+7 , а раскрытие скобок в выражении 3+(4+7) приведет нас к выражению 3+4+7 , здесь перед слагаемым 4 мы поставили знак плюс, так как оно является первым слагаемым в скобках и записано в них без знака.

Для закрепления материала покажем еще один пример раскрытия скобок: .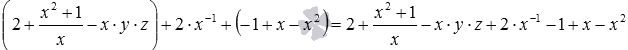

Как раскрываются скобки, перед которыми стоит знак −

Переходим к раскрытию скобок, перед которыми стоит знак минус, и которые не умножаются (или делятся) на какое-либо число или выражение. Дадим соответствующее правило.

Сформулируем правило раскрытия скобок, перед которыми стоит знак минус: скобки вместе со знаком минус опускаются, а знаки всех слагаемых в скобках заменяются на противоположные.

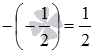
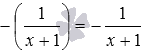
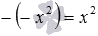
Выше мы уже сталкивались с выражениями вида −(a) и −(−a) , которые без скобок записываются как −a и a соответственно. Например, −(3)=3 , , и . Это частные случаи озвученного правила.

Теперь рассмотрим примеры раскрытия скобок, когда в них заключены суммы или разности. Например, выражение −(−9+5) после раскрытия скобок примет вид 9−5 , здесь мы опустили скобки со знаком минус перед ним, заменив знаки слагаемых на противоположные. Еще пример: 5+2,2−(6−2/3−4,1+11)+2= 5+2,2−6+2/3+4,1−11+2 .

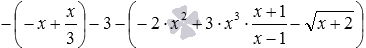
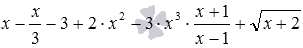
Это же правило применяется при раскрытии скобок, перед которыми стоит знак минус, и которые содержат выражения с переменными. Для примера раскроем скобки в выражении с переменными вида , имеем .

Раскрытие скобок при умножении числа на скобку, выражения на скобку

В двух предыдущих пунктах мы говорили о раскрытии скобок, которые не умножаются на какое-либо число или выражение. Сейчас мы как раз перейдем к раскрытию скобок в выражениях, в которых выражение в скобках умножается на число или выражение.

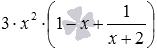
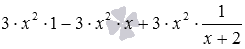
Покажем примеры использования этого правила. Раскроем скобки в выражении (3−7)·2 . По записанному правилу получаем (3−7)·2=(3·2−7·2) , последние выражение по правилу раскрытия скобок, перед которыми не стоит никакого знака, принимает вид 3·2−7·2 . Еще пример: возьмем выражение , после раскрытия скобок получаем .

Умножение скобки на скобку

Используя правило из предыдущего пункта, можно получить правило раскрытия скобок при умножении скобки на скобку. Чтобы оно легко воспринялось, рассмотрим произведение двух скобок вида (a₁+a₂)·(b₁+b₂) .

Так мы от произведения двух скобок пришли к сумме произведений каждого слагаемого из первой скобки на каждое слагаемое из второй скобки. По индукции это утверждение можно распространить на произвольное количество слагаемых в каждой скобке.

Теперь можно дать формулировку правила умножения скобки на скобку. Оно звучит так: чтобы умножить одну сумму на другую, надо каждое слагаемое первой суммы умножить на каждое слагаемое второй суммы и сложить полученные произведения. Запишем соответствующую формулу:

Для примера раскроем скобки в выражении (1+x)·(x 2 +x+6) , представляющим собой произведение двух сумм. Для этого записываем сумму произведений первого слагаемого 1 из первой скобки на каждое слагаемое x 2 , x и 6 из второй скобки, а также второго слагаемого x из первой скобки на каждое слагаемое x 2 , x и 6 из второй скобки, получаем (1+x)·(x 2 +x+6)= (1·x 2 +1·x+1·6+x·x 2 +x·x+x·6)= 1·x 2 +1·x+1·6+x·x 2 +x·x+x·6 .

Стоит отдельно заметить, что если в скобках наряду со знаками плюс присутствуют знаки минус, то выражения в скобках перед использованием записанного выше правила нужно представить в виде сумм. Покажем это на примере.

Раскроем скобки в выражении (1−x)·(3·x·y−2·x·y 3 ) . Перед использованием правила нужно выражения в скобках представить в виде сумм как (1+(−x))·(3·x·y+(−2·x·y 3 )) . Теперь умножаем скобку на скобку: (1+(−x))·(3·x·y+(−2·x·y 3 ))= (1·3·x·y+1·(−2·x·y 3 )+ (−x)·3·x·y+(−x)·(−2·x·y 3 )) . Осталось раскрыть скобки в полученном выражении, используя правила из предыдущих пунктов, в итоге получаем 1·3·x·y−1·2·x·y 3 −x·3·x·y+x·2·x·y 3 .

Раскрытие скобок в произведениях нескольких скобок и выражений

Раскрытие скобок в выражениях, которые представляют собой произведение трех и большего количества выражений в скобках, проводится последовательно. Сначала берутся два первых множителя, заключаются еще в одни скобки, и внутри этих скобок проводится раскрытие скобок по одному из уже известных правил. И этот процесс продолжается.

Лучше разобраться с этим на примере. Раскроем скобки в выражении (2+4)·3·(5+7·8) . Это выражение представляет собой произведение трех множителей (2+4) , 3 и (5+7·8) . Раскрывать скобки придется последовательно. Для этого заключаем первые два множителя еще в одни скобки, для наглядности изобразим их другим цветом: (2+4)·3·(5+7·8)= ( (2+4)·3 ) ·(5+7·8) . Теперь используем правило умножения скобки на число, имеем ( (2+4)·3 ) ·(5+7·8)= ( 2·3+4·3 ) ·(5+7·8) . Осталось выполнить умножение скобки на скобку: ( 2·3+4·3 ) ·(5+7·8)= 2·3·5+2·3·7·8+4·3·5+4·3·7·8 .

Понятно, что вместо чисел могут быть и переменные, и другие выражения.

Скобка в натуральной степени

Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.

Для примера преобразуем выражение (a+b+c) 2 . Сначала запишем его в виде произведения двух скобок (a+b+c)·(a+b+c) , теперь выполним умножение скобки на скобку, получаем a·a+a·b+a·c+b·a+b·b+b·c+c·a+c·b+c·c .

Стоит отметить, что подобные преобразования более уместно называть возведением выражения в степень, нежели раскрытием скобок.

Вот еще пример возведения выражения в скобках в третью степень:

Также скажем, что для возведения сумм и разностей двух чисел в натуральную степень целесообразно применять формулу бинома Ньютона.

Деление скобки на число и скобки на скобку

В этом пункте мы покажем, как стоит раскрывать скобки в выражениях, в которых имеет место деление скобки на число или выражение.

При делении скобки на число можно раскрыть скобки, разделив на это число каждое из заключенных в скобки слагаемых.

К примеру, (5+7−3):2=5:2+7:2−3:2 . Вот еще пример раскрытия скобок при делении выражения на число: .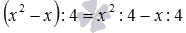

Не менее удобно предварительно деление заменить умножением, после чего воспользоваться соответствующим правилом раскрытия скобок в произведении. Это правило позволяет раскрывать скобки и при делении скобки на скобку.

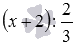
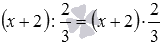
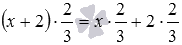
Приведем примеры. Раскроем скобки в выражении . Заменим сначала деление умножением на обратное число, имеем . Осталось выполнить умножение скобки на число, получаем .

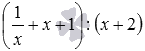
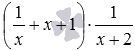
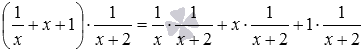
Покажем еще пример, рассмотрев выражение, в котором содержится деление на скобку, вида . Заменяем деление умножением: . И осталось лишь выполнить умножение: .

И прежде чем перейти к следующему разделу информации стоит сказать, что все перечисленные правила раскрытия скобок следуют из правил выполнения действий с числами, а также правил использования скобок в математике.

Порядок раскрытия скобок

Вот мы и добрались до раздела, который объясняет, как с помощью всей представленной выше информации выполняется раскрытие скобок в выражениях общего вида, то есть, в выражениях, содержащих и суммы с разностями, и произведения с частными, и скобки в натуральной степени.

В таких выражениях порядок раскрытия скобок согласован с порядком выполнения действий:

• сначала выполняется возведение скобок в натуральную степень,
• дальше раскрываются скобки в произведениях и частных,
• наконец, когда скобок в произведениях не остается, раскрываются скобки в суммах и разностях.

Осталось разобраться с порядком раскрытия скобок на примерах.

Возьмем выражение (−5)+3·(−2):(−4)−6·(−7) . Раскрытие скобок нужно начинать с выражений 3·(−2):(−4) и 6·(−7) , после применения соответствующих правил раскрытия скобок, они примут вид (3·2:4) и (−6·7) . Подставляем эти результаты в исходное выражение: (−5)+3·(−2):(−4)−6·(−7)= (−5)+(3·2:4)−(−6·7) . Остается лишь закончить раскрытие скобок, в результате имеем −5+3·2:4+6·7 .

Как Вы заметили, мы исходное выражение разбили на составные части, в каждой части провели раскрытие скобок по разобранным правилам, после чего собрали полученные результаты воедино, и пришли к требуемому результату.

Раскрытие скобок в выражениях, содержащих скобки в скобках, удобно проводить, продвигаясь от внутренних скобок к внешним.

В заключение статьи заметим, что раскрытие скобок в основном применяется при упрощении выражений, и в сложных выражениях раскрытие скобок проводится вместе с другими преобразованиями до получения нужного результата.

Источник