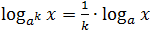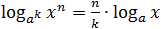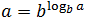Как избавится от степени логарифма

Основные свойства логарифмов

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log _a x и log _a y . Тогда их можно складывать и вычитать, причем:

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log₆ 4 + log₆ 9 = log₆ (4 · 9) = log₆ 36 = 2.

Основания одинаковые, используем формулу разности:
log₂ 48 − log₂ 3 = log₂ (48 : 3) = log₂ 16 = 4.

Задача. Найдите значение выражения: log₃ 135 − log₃ 5.

Снова основания одинаковые, поэтому имеем:
log₃ 135 − log₃ 5 = log₃ (135 : 5) = log₃ 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

1. log _a x n = n · log _a x ;
2. 
3. 

Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Задача. Найдите значение выражения: log₇ 49 6 .

Избавимся от степени в аргументе по первой формуле:
log₇ 49 6 = 6 · log₇ 49 = 6 · 2 = 12

Задача. Найдите значение выражения:

[Подпись к рисунку]

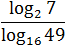
Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 2 4 ; 49 = 7 2 . Имеем:

[Подпись к рисунку]

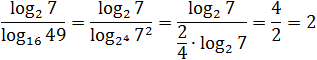
Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log₂ 7. Поскольку log₂ 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

Пусть дан логарифм log _a x . Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:

[Подпись к рисунку]

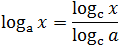
В частности, если положить c = x , получим:

[Подпись к рисунку]

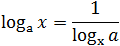
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача. Найдите значение выражения: log₅ 16 · log₂ 25.

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log₅ 16 = log₅ 2 4 = 4log₅ 2; log₂ 25 = log₂ 5 2 = 2log₂ 5;

А теперь «перевернем» второй логарифм:

[Подпись к рисунку]

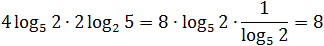
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Задача. Найдите значение выражения: log₉ 100 · lg 3.

Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:

[Подпись к рисунку]

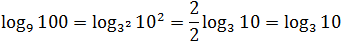
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:

[Подпись к рисунку]

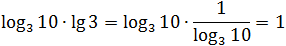
Основное логарифмическое тождество

Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

1. n = log _a a n
2. 

В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.

Вторая формула — это фактически перефразированное определение. Она так и называется: .

В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a ? Правильно: получится это самое число a . Внимательно прочитайте этот абзац еще раз — многие на нем «зависают».

Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.

Задача. Найдите значение выражения:

[Подпись к рисунку]

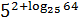
Заметим, что log₂₅ 64 = log₅ 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:

[Подпись к рисунку]

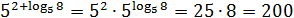
Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂

Логарифмическая единица и логарифмический ноль

В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

1. log _a a = 1 — это . Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
2. log _a 1 = 0 — это . Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a 0 = 1 — это прямое следствие из определения.

Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.

Источник

Как избавиться от логарифмов — математический — 2021

Ничто так не портит уравнение, как логарифмы. Они громоздки, трудны для манипуляции и немного загадочны для некоторых людей. К счастью, есть простой способ избавить ваше уравнение от этих надоедливых математических выражений. Все, что вам нужно сделать, это помнить, что логарифм является обратным показателю степени. Хотя основание логарифма может быть любым числом, наиболее распространенные основания, используемые в науке, это 10 и е, что является иррациональным числом, известным как число Эйлера. Чтобы отличить их, математики используют «log», когда основание равно 10, и «ln», когда основание равно e.

TL; DR (слишком долго; не читал)

Чтобы избавиться от уравнения логарифмов, возведите обе стороны к тому же показателю, что и основание логарифмов. В уравнениях со смешанными терминами соберите все логарифмы с одной стороны и сначала упростите.

Что такое логарифм?

Концепция логарифма проста, но это немного сложно выразить словами. Логарифм — это количество раз, которое вам нужно умножить число, чтобы получить другое число. Другой способ сказать, что логарифм — это степень, до которой определенное число, называемое основанием, должно быть поднято, чтобы получить другое число. Сила называется аргумент логарифма.

Например, log ₈ 2 = 64 просто означает, что повышение 8 до степени 2 дает 64. В уравнении log x = 100 основание понимается как 10, и вы можете легко решить для аргумента x, потому что он отвечает вопрос «10 поднял до какой силы равна 100?» Ответ 2.

Логарифм является обратным показателю степени. Уравнение log x = 100 — это другой способ записи 10 x = 100. Это соотношение позволяет удалить логарифмы из уравнения, подняв обе стороны до того же показателя, что и основание логарифма. Если уравнение содержит более одного логарифма, они должны иметь одну и ту же базу, чтобы это работало.

Примеры

В простейшем случае логарифм неизвестного числа равен другому числу: log x = y. Поднимите обе стороны до показателей 10, и вы получите 10 (log x) = 10 y . Поскольку 10 (log x) — это просто x, уравнение становится x = 10 y .

Когда все члены в уравнении являются логарифмами, возведение обеих сторон в степень дает стандартное алгебраическое выражение. Например, возведите log (x 2 — 1) = log (x + 1) до степени 10, и вы получите: x 2 — 1 = x + 1, что упрощается до x 2 — x — 2 = 0. Решения х = -2; х = 1

В уравнениях, которые содержат смесь логарифмов и других алгебраических терминов, важно собрать все логарифмы на одной стороне уравнения. Затем вы можете добавить или вычесть условия. Согласно закону логарифмов, верно следующее:

• log x + log y = log (xy)
• log x — log y = log (x ÷ y)

Вот процедура для решения уравнения со смешанными членами:

1. Начните с уравнения: например, log x = log (x — 2) + 3
2. Переставьте термины: log x — log (x — 2) = 3
3. Применим закон логарифмов: log (x / x-2) = 3
4. Поднимите обе стороны до степени 10: x ÷ (x — 2) = 3
5. Решите для х: х= 3

Расчет логарифмов

Логарифм — это математическая функция, тесно связанная с экспонентами. На самом деле логарифм является инверсией экспоненциальной функции. Общая форма — log_b (x), которая читает «log base b of x». Часто log без оснований подразумевает log 10 log_10, а ln ссылается на «натуральный log» log_e, где e — это .

Как избавиться от кислоты

Как избавиться от кислоты. За определенный период времени большинство из нас накопили несколько отходов, которые имеют кислую природу. Не стоит избавляться от этих вещей, просто выливая их на землю, чтобы смыть следующим дождем. В большинстве случаев фактически закон запрещает распоряжаться этими продуктами в .

Как избавиться от хлорида кальция

Хлорид кальция — это соль кальция и хлора. Он используется в аквариумах с морской водой и на дорогах для таяния льда. Обычно это не опасно и может быть утилизировано в мусорном ведре или в канализацию.

Источник

Логарифм. Свойства логарифма (степень логарифма).

Свойства логарифма получаются из его определения. Общеизвестный факт, что логарифм числа b по основанию а определяется как показатель степени, в которую надо возвести число a, чтобы получить число b.

Из формулировки получаем очевидные равенства log_a1 = 0 так как а 0 =1 и, log_aа = 1 так как а 1 =а.

Рассмотрим ситуации, когда в основании или аргументе логарифма стоит степень. Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

Конечно же, все эти формулы будут иметь смысл при соблюдении области действующих значений логарифма: a > 0, a ≠ 1, x > 0. И еще: ими всеми можно пользоваться не только слева направо, но и наоборот, а значит разрешено перемещать числа, стоящие перед знаком логарифма в сам логарифм. Собственно это чаще всего и делается.

Логарифм степени положительного числа равен произведению показателя этой степени на логарифм ее основания:

Или если сказать проще, в данном случае показатель степени выносится как сомножитель, в результате трудоемкое действие возведения в степень меняем на более элементарную операцию умножения.

При отрицательных значениях х формула становиться бессмысленной. Так, запрещено писать log₂(- 4) 2 = 2log₂ (- 4), так как выражение log₂(- 4) не определено. Однако обратим внимание, что выражение, стоящее в левой части этой формулы, все же имеет смысл:

Источник