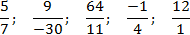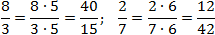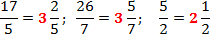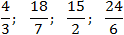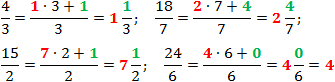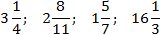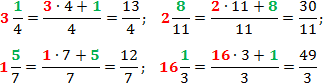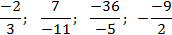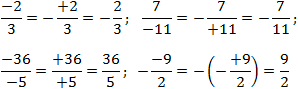Как избавиться от целого числа перед дробью

Калькулятор дробей

Как перевести смешанную дробь в обыкновенную

Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i n d = i · d + n d

5 3 4 = 5 · 4 + 3 4 = 23 4

Как перевести обыкновенную дробь в смешанную

Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:

1. Поделить числитель дроби на её знаменатель
2. Результат от деления будет являться целой частью
3. Остаток отделения будет являться числителем

Как перевести обыкновенную дробь в десятичную

Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.

Как перевести десятичную дробь в обыкновенную или смешанную

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:

1. Записать дробь в виде десятичная дробь 1
2. Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
3. Найти наибольший общий делитель и сократить дробь.

Например, переведем 0.36 в обыкновенную дробь:

1. Записываем дробь в виде: 0.36 1
2. Умножаем на 10 два раза, получим 36 100
3. Сокращаем дробь 36 100 = 9 25

Как перевести дробь в проценты

Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.

Как перевести проценты в дробь

Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.

Сложение дробей

Алгоритм действий при сложении двух дробей такой:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Выполнить сложение дробей путем сложения их числителей.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Вычитание дробей

Алгоритм действий при вычитании двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Умножение дробей

Алгоритм действий при умножении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
3. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
4. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Деление дробей

Алгоритм действий при делении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
3. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Источник

Что такое числовая дробь

Хотите почувствовать себя сапером? Тогда этот урок — для вас! Потому что сейчас мы будем изучать дроби — это такие простые и безобидные математические объекты, которые по способности «выносить мозг» превосходят весь остальной курс алгебры.

Главная опасность дробей состоит в том, что они встречаются в реальной жизни. Этим они отличаются, например, от многочленов и логарифмов, которые можно пройти и спокойно забыть после экзамена. Поэтому материал, изложенный в данном уроке, без преувеличения можно назвать взрывоопасным.

(или просто дробь) — это пара целых чисел, записанных через косую или горизонтальную черту.

Дроби, записанные через горизонтальную черту:

Те же самые дроби, записанные через косую черту:
5/7; 9/(−30); 64/11; (−1)/4; 12/1.

Обычно дроби записываются через горизонтальную черту — так с ними проще работать, да и выглядят они лучше. Число, записанное сверху, называется числителем дроби, а записанное снизу — знаменателем.

Любое целое число можно представить в виде дроби со знаменателем 1. получилась дробь из приведенного выше примера.

Вообще, в числитель и знаменатель дроби можно поставить любое целое число. Единственное ограничение — знаменатель должен быть отличен от нуля. Вспомните старое доброе правило: «На ноль делить нельзя!»

Если в знаменателе все-таки стоит ноль, дробь называется неопределенной. Такая запись не имеет смысла и не может участвовать в вычислениях.

Основное свойство дроби

Дроби a / b и c / d называются ,

Из этого определения следует, что одну и ту же дробь можно записать по-разному. Например, , поскольку 1 · 4 = 2 · 2. Разумеется, существует множество дробей, которые не равны друг другу. Например, , поскольку 1 · 4 ≠ 3 · 5.

Возникает резонный вопрос: как найти все дроби, равные данной? Ответ дадим в форме определения:

— числитель и знаменатель можно умножать на одно и то же число, отличное от нуля. При этом получится дробь, равная данной.

Это очень важное свойство — запомните его. С помощью основного свойства дроби можно упрощать и сокращать многие выражения. В будущем оно постоянно будет «всплывать» в виде различных свойств и теорем.

Неправильные дроби. Выделение целой части

Если числитель меньше знаменателя, такая дробь называется правильной. В противном случае (т.е. когда числитель больше или хотя бы равен знаменателю) дробь называется неправильной, и в ней можно выделить целую часть.

Целая часть записывается крупным числом спереди перед дробью и выглядит так (отмечена красным):

Чтобы выделить целую часть в неправильной дроби, надо выполнить три простых шага:

1. Найдите, сколько раз знаменатель помещается в числителе. Другими словами, найдите максимальное целое число, которое при умножении на знаменатель все равно будет меньше числителя (в крайнем случае — равно). Это число и будет целой частью, поэтому записываем его спереди;
2. Умножьте знаменатель на целую часть, найденную в предыдущем шаге, а результат вычтите из числителя. Полученный «огрызок» называется остатком от деления, он всегда будет положительным (в крайнем случае — ноль). Записываем его в числитель новой дроби;
3. Знаменатель переписываем без изменений.

Ну как, сложно? На первый взгляд, может быть и сложно. Но стоит немного потренироваться — и вы будете делать это почти устно. А пока взгляните на примеры:

Задача. Выделите целую часть в указанных дробях:

Во всех примерах целая часть выделена красным цветом, а остаток от деления — зеленым.

Обратите внимание на последнюю дробь, где остаток от деления оказался равным нулю. Получается, что числитель полностью разделился на знаменатель. Это вполне логично, ведь 24 : 6 = 4 — суровый факт из таблицы умножения.

Если все делать правильно, числитель новой дроби обязательно будет меньше знаменателя, т.е. дробь станет правильной. Отмечу также, что лучше выделять целую часть в самом конце задачи, перед записью ответа. Иначе можно значительно усложнить вычисления.

Переход к неправильной дроби

Существует и обратная операция, когда мы избавляемся от целой части. Она называется переходом к неправильной дроби и встречается намного чаще, поскольку работать с неправильными дробями значительно проще.

Переход к неправильной дроби также выполняется в три шага:

1. Умножить целую часть на знаменатель. В результате могут получаться довольно большие числа, но нас это не должно смущать;
2. Прибавить полученное число к числителю исходной дроби. Результат записать в числитель неправильной дроби;
3. Переписать знаменатель — опять же, без изменений.

Вот конкретные примеры:

Задача. Переведите в неправильную дробь:

Для наглядности целая часть снова выделена красным цветом, а числитель исходной дроби — зеленым.

Вынесение минуса за знак дроби

Рассмотрим случай, когда в числителе или знаменателе дроби стоит отрицательное число. Например:

В принципе, ничего криминального в этом нет. Однако работать с такими дробями бывает неудобно. Поэтому в математике принято выносить минусы за знак дроби.

Сделать это очень просто, если вспомнить правила:

1. «Плюс на минус дает минус». Поэтому если в числителе стоит отрицательное число, а в знаменателе — положительное (или наоборот), смело зачеркиваем минус и ставим его перед всей дробью;
2. «Минус на минус дает плюс». Когда минус стоит и в числителе, и в знаменателе, просто зачеркиваем их — никаких дополнительных действий не требуется.

Разумеется, эти правила можно применять и в обратном направлении, т.е. можно вносить минус под знак дроби (чаще всего — в числитель).

Случай «плюс на плюс» мы намеренно не рассматриваем — с ним, думаю, и так все понятно. Лучше посмотрим, как эти правила работают на практике:

Задача. Вынесите минусы из четырех дробей, записанных выше.

Обратите внимание на последнюю дробь: перед ней уже стоит знак минус. Однако он «сжигается» по правилу «минус на минус дает плюс».

Также не стоит перемещать минусы в дробях с выделенной целой частью. Эти дроби сначала переводят в неправильные — и лишь затем приступают к вычислениям.

Источник

Как вычитать дробь из целого числа

Вначале рассмотрим, как обыкновенную дробь вычесть из единицы.

Мы знаем, что число 1 мы можем представить в виде дроби с любым знаменателем. Причем, у этой дроби и числитель, и знаменатель будут одинаковые числа.

Поэтому, чтобы из 1 вычесть 2/5, надо 1 представить как 5/5, т.е. с таким же знаменателем, как и вычитаемая дробь. А затем выполнить действие: 5/5 – 2/5 = 3/5, значит, 1 – 2/5 = 3/5

Как вычесть дробь из целого числа, отличного от 1?

Вычитать можно несколькими способами.

1 способ:

1) представим число 5 в виде дробь: 5/1, получится 5/1 – 3/4;

2) 5/1 и 3/4 – дроби с разными знаменателями, поэтому приводим в общему знаменателю (см. статью здесь): 20/4 и 3/4;

3) выполняем вычитание: 20/4 – 3/4 = 17/4;

4) 17/4 – это неправильная дробь, поэтому переводим в смешанное число: 17/4 = 4 ¼

5) Итак: 5 – 3/4 = 4 ¼

2 способ:

1) мы уже умеем вычитать дробь из единицы, поэтому из нашего числа 5 занимаем единицу, остается 4 целых;

2) а из единицы вычитаем 3/4 = 1/4;

3) к 4 целым прибавляем 1/4, получаем 4 ¼

Для работы с дробями – выбираем удобный для себя способ!

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 65

Источник

Вычитание дробей

При вычитании дробей, как и при сложении, могут встретиться несколько случаев.

Вычитание дробей с одинаковыми знаменателями

При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.

Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.

В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так:

Вычитание правильной дроби из единицы

Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.

Знаменатель вычитаемой дроби равен 7 , значит, единицу представляют как неправильную дробь

7

7

и вычитают по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа

Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число в виде смешанного числа.

Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби, знаменатель которой равен знаменателю вычитаемой дроби.

В примере единицу мы заменили неправильной дробью

7

7

и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание смешанных чисел

При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.

При подобных расчётах могут встретиться разные случаи.

Первый случай вычитания смешанных чисел

У дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого (что вычитаем).

Второй случай вычитания смешанных чисел

У дробных частей разные знаменатели.

В этом случае вначале нужно привести к общему знаменателю дробные части, а затем выполнить вычитание целой части из целой, а дробной из дробной.

Третий случай вычитания смешанных чисел

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Так как у дробных частей разные знаменатели, то как и во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.

Сложим полученную неправильную дробь

18

18

и дробную часть уменьшаемого и получим:

Все рассмотренные случаи можно описать с помощью правил вычитания смешанных чисел.

• Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
• Если дробная часть уменьшаемого меньше дробной части вычитаемого, то занимаем у целой части уменьшаемого единицу. Эту единицу превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю.
• Прибавляем полученную неправильную дробь к дробной части уменьшаемого.
• Вычитаем из целой части целую, а из дробной — дробную.
• Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.

Источник