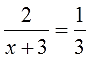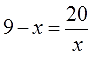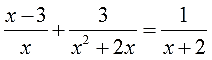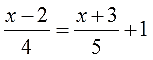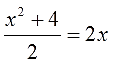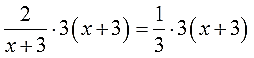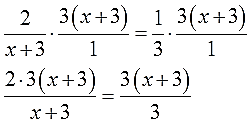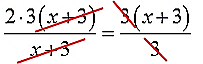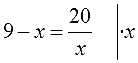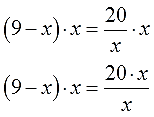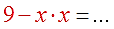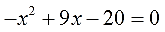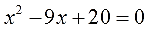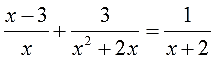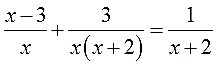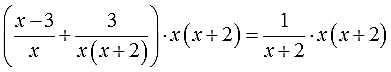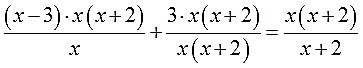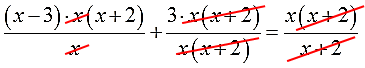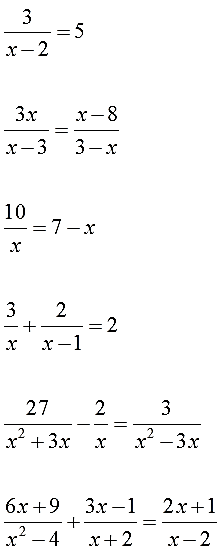Как избавиться от знаменателя дроби пример

Как решать дробные уравнения?

Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.

Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)

Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:

1. Дроби и действия с дробями и дробными выражениями.

3. Решение линейных и квадратных уравнений.

Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т.д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)

Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.

Что такое дробное уравнение? Примеры.

Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.

Например, вот такое уравнение:

И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.

Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.

Или такое уравнение:

Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.

В общем, вы поняли.

Как решать дробные уравнения? Убираем дроби!

Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?

Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)

Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?

Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)

Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:

Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.

А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?

Давайте его конструировать.) Смотрим ещё раз на уравнение:

Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)

Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.

Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).

Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:

Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!

А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:

Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:

А его (надеюсь) уже решит каждый:

Решаем следующий примерчик:

И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.

Вот и домножаем! Всю левую часть и всю правую часть:

Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».

А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!

Дело всё в том, что частенько после умножения народ записывает левую часть вот так:

Это категорически неверно. Дальше можно уже не решать, да…)

Но у нас всё хорошо, будем дорешивать.

С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.

Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:

Переносим всё влево и приводим к стандартному виду:

Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:

Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:

Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.

А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.

Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…

Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)

Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.

Раскладываем на множители!

Решаем третье уравнение по списку:

А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить

и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?

Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)

А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х 2 +2х вполне себе раскладывается! Выносим один икс за скобку и получаем:

Отлично. Вставим наше разложение в исходное уравнение:

Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).

Вот на х(х+2) и умножаем:

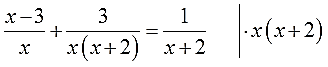
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:

А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:

Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)

С удовольствием сокращаем все дроби:

Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:

И снова получили квадратное уравнение.) Решаем и получаем два корня:

Вот и всё. Это и есть ответ.)

Из этого примера можно сделать важный вывод:

Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!

Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)

Ну что, порешаем?)

Ответы (как обычно, вразброс):

Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)

Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!

Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…

Источник

Преобразование рациональных (алгебраических) дробей: виды преобразований, примеры

Виды выражений из алгебры могут принимать вид рациональных дробей, которые характерны тождественным преобразованиям этих дробей. Чаще всего можно встретить еще одно название алгебраические дроби. Таким образом, понятия рациональных и алгебраических дробей равнозначны.

Рассмотрим приведение рациональной дроби к новому знаменателю, смене знаков, сокращению. Подробно остановимся на преобразовании дробей в виде суммы с несколькими показателями. В заключении приведем несколько примеров, в которых подробно рассмотрим решения.

Определение и примеры рациональных дробей

Рациональная дробь – это дробь,в числителе и знаменателе которой, имеются многочлены с натуральными, целыми и рациональными коэффициентами.

Многочлены могут быть приведены в нестандартном виде, что говорит о том, что необходимы дополнительные преобразования.

Рассмотрим примеры рациональных дробей.

— 2 a 2 · b — b , x + 2 , 3 · x + 2 2 3 · x 2 · y · z x 2 + y 2 + z 2 , х 8 , 1 4 · x 2 — 3 · x + 1 2 · x + 3 считаются рациональными дробями.

А 5 · ( x + y ) · y 2 — x 4 · y и a b — b a 3 + 1 a + 1 a 2 не являются таковыми, так как не имеют выражений с многочленами.

Преобразования числителя и знаменателя рациональной дроби

Числитель и знаменатель считаются самодостаточными числовыми выражениями. Отсюда следует, что с ними можно производить различные преобразования, то есть в числителе или знаменателе разрешено заменять на тождественное равное ему выражение.

Чтобы провести тождественные преобразования, необходимо группировать и приводить подобные слагаемые, причем знаменатель заменять на более простое подобное ему выражение. Числители и знаменатели содержат многочлены, значит, что с ними можно производить преобразования, подобные для многочленов. Это могут быть и приведения к стандартному виду или представление в виде произведения.

Преобразовать 3 · a — a · b — 2 · b · 5 6 · b + 2 3 7 · a · b a 3 · b 2 — 5 · a 2 · b + 3 · a · b — 15 таким образом, чтобы числитель получил стандартный вид многочлена, а знаменатель – их произведение.

Для начала необходимо привести к стандартному виду. Применим свойство степени, получим выражение вида

3 · a — a · b — 2 · b · 5 6 · b + 2 3 7 · a · b = 3 · a — a · b — 5 3 · b 2 + 2 3 7 · a · b = = 3 · a + — α · b + 2 3 7 · a · b — 5 3 · b 2 = 3 · a + 1 3 7 · a · b — 5 3 · b 2

Необходимо выполнить преобразования знаменателя. Представляем его в виде произведения, то есть раскладываем на многочлены. Для этого производим группировку первого и третьего слагаемых, а второго с четвертым. Общий множитель выносим за скобки и получаем выражение вида

a 3 · b 2 — 5 · a 2 · b + 3 · a · b — 15 = ( a 3 · b 2 + 3 · a · b ) + ( — 5 · a 2 · b — 15 ) = = a · b · ( a 2 · b + 3 ) — 5 · ( a 2 · b + 3 )

Видно, что полученное выражение имеет общий множитель, который и необходимо вынести за скобки, чтобы получить

a · b · ( a 2 · b + 3 ) — 5 · ( a 2 · b + 3 ) = a 2 · b + 3 · ( a · b — 5 )

Теперь подходим к произведению многочленов.

Проведя преобразования, получаем, что заданная дробь принимает вид 3 · a + 1 3 7 · a · b — 5 3 · b 2 a 2 · b + 3 · ( a · b — 5 ) .

Ответ: 3 · a — a · b — 2 · b · 5 6 · b + 2 3 7 · a · b a 3 · b 2 — 5 · a 2 · b + 3 · a · b — 15 = 3 · a + 1 3 7 · a · b — 5 3 · b 2 a 2 · b + 3 · ( a · b — 5 ) .

Данные преобразования необходимы для их использования в преобразованиях.

Приведение к новому знаменателю

При изучении обыкновенных дробей знакомимся с основным свойством дроби, которое говорит о том, что при умножении числителя и знаменателя на любое натуральное число, получаем равную предыдущей дробь. Данное свойство распространяется и на рациональные дроби: при умножении на ненулевой многочлен числитель и знаменатель, получим дробь, равную предыдущей.

Для любых многочленов a , b и c , где b и c являются ненулевыми, равенство вида a b = a · c b · c справедливо, тогда они являются тождеством. К примеру, x · y + 1 2 · x — 5 = ( x · y + 1 ) · ( x 2 + 3 · b 2 ) ( 2 · x — 5 ) · ( x 2 + 3 · b 2 ) является справедливым для всей ОДЗ переменных x и y .

Отсюда следует то, что при решении необходимо воспользоваться приведением рациональной дроби к новому знаменателю. То есть ее умножение и числителя и знаменателя на ненулевой многочлен. В результате получим дробь, равную заданной.

Если рассмотреть такой пример рациональной дроби вида x — y 2 · x , то при приведении к новому знаменателю, получим новую, но равную предыдущей. Необходимо умножить числитель и знаменатель на выражение x 2 + y , тогда имеем, что выражение x — y · x 2 + y 2 · x · ( x 2 + y ) при помощи преобразования примет вид рациональной дроби x 3 + x · y — x 2 · y — y 2 2 · x 3 + 2 · x · y . Такие приведения используются для сложения или вычитания дробей. Углубить знания можно в разделе приведения алгебраических дробей к новому знаменателю.

Изменение знаков перед дробью, в ее числителе и знаменателе

Основное свойство дроби применяется для того, чтобы можно было сменить знаки у членов дроби. Эти преобразования характерны для рациональных дробей.

При одновременном изменении знаков у числителя и знаменателя получаем дробь, равную заданной. Это утверждение запишем так — a — b = a b .

Дробь вида — x — 2 x — y заменяют равной ей x + 2 y — x .

При работе с дробями можно менять знак только в числителе или только в знаменателе. При замене знака дроби, получаем тождественно равную дробь. Запишем это утверждение так:

a b = — — a b и a b = — a — b .

Для доказательства используется первое свойство. Получаем, что — — a b = — ( ( — a ) : b ) = ( — 1 ) · ( ( ( — 1 ) · a ) : b ) = ( — 1 ) · ( — 1 ) · a : b = a : b = a b .

При помощи преобразований доказывается равенство вида a b = — a — b .

К примеру, x x — 1 заменяем — — x x — 1 или — x 1 — x .

Существуют два полезных равенства вида — a b = — a b и a — b = — a b . Отсюда замечаем, что при изменении знака в числителе или только в знаменателе, изменится знак дроби. Получаем, — 3 x 3 · y + z = — 3 x 3 · y + z и x + 3 — x + 5 = — x + 3 x — 5 .

Чаще всего такие преобразования подходят для дробно рациональных выражений и их преобразований.

Сокращение рациональных дробей

Основа преобразования – это свойство дроби. То есть применяется a · c b · c = a b , где имеем, что a , b и c являются некоторыми многочленами, где b и c – нулевые.

Сократить дробь 2 · x 2 · y 3 2 · x · y 7 .

Заметим, что 2 является общим множителем, значит необходимо сократить на него выражение. Получим, что 2 · x 2 · y 3 2 · x · y 7 = 2 · x 2 · y 3 2 · x · y 7 = x 2 · y 3 x · y 7 . Видно, что x 2 = x · x и y 7 = y 3 · y 4 , тогда x – это общий множитель. После сокращения получим, что x 2 · y 3 x · y 7 = ( x · x ) · y 3 x · ( y 3 · y 4 ) = x y 4 . Сокращение выполняется последовательно, что позволяет получать точные ответы 2 · x 2 · y 3 2 · x · y 7 = ( 2 · x · y 3 ) · x ( 2 · x · y 3 ) · y 4 = x y 4 .

Ответ: 2 · x 2 · y 3 2 · x · y 7 = x y 4 .

Не всегда виден общий знаменатель при сокращении. Это и есть небольшая проблема. Не всегда это возможно увидеть сразу. Возможно, необходимо будет выполнить разложение числителя и знаменателя на множители. Это упростит решение. Подробно нюансы рассмотрены в теме сокращения алгебраических дробей.

При сокращении важно обратить внимание на то, что чаще всего необходимо раскладывать и числитель и знаменатель на множители.

Представление рациональной дроби в виде суммы дробей

Если имеется несколько дробей, то преобразование производится особым образом. Такую рациональную дробь необходимо представить в виде выражения, где имеются одночлены.

К примеру, 3 · a 2 + a · b — 5 a + b = 3 · a 2 a + b + a · b a + b — 5 a + b .

Это основано на правиле сложения и вычитания дробей с одинаковыми знаменателями.

Любая рациональная дробь представляется в виде суммы дробей разными способами. Запишем это в виде утверждения a b = c d + a b — c d . Если x · y — x x + 1 представлять в виде суммы дробей, тогда получаем выражения вида

x · y — x x + 1 = 1 x + x 2 · y — x 2 — x — 1 x 2 + x , x · y — x x + 1 = x x — 1 + x 2 · y — x · y — 2 x 2 x 2 — 1 и так далее.

В особую группу выделяют представления рациональных дробей с одной переменной. Когда показатель такой дроби больше или равен степени показателя знаменателя, тогда переходим к преобразованию суммы рационального выражения. То есть выполняется деления многочлена на многочлен.

Какие значения n являются целым числом дроби n 4 — 2 · n 3 + 4 · n — 5 n — 2 ?

Необходимо представить исходную дробь в виде суммы выражений и дроби. После деления числителя и знаменателя, получим выражение вида n 4 — 2 · n 3 + 4 · n — 5 n — 2 = n 3 + 4 + 3 n — 2 . Отсюда видно, что n 3 + 4 при любом n будет целым числом. А дробь 3 n — 2 принимает целые значения при n = 3 , n = 1 , n = 5 и n = − 1 .

Источник