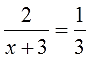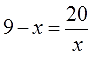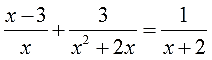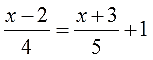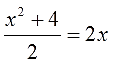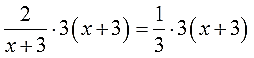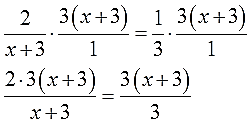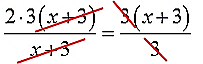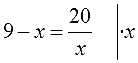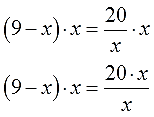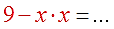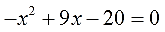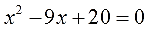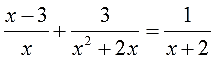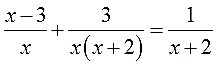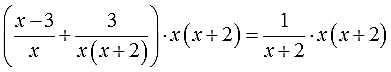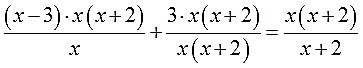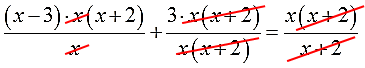Решение неравенств. Общие соображения.
Свойства числовых неравенств
Для любых дейcтвительных чисел a, b, c и d выполняются следующие свойства:
Другими словами, если обе части верного неравенства умножить на одно и то же положительное число, то знак неравенства не изменится, неравенство останется верным.
Если почленно сложить два верных неравенства одного знака, то получится верное неравенство.
Следующие свойства выполняются только для положительных чисел.
Если a >b > 0 и с >d > 0, то ac >bd.
Почленно перемножать можно неравенства одного знака только тогда, когда левая и правая части обоих нервенств положительны.
Особое внимание обратите на свойства 5 и 9. Они непосредственно связаны с нашей темой — дробно-рациональные неравенства.
Напомню, что рациональными называются выражения, которые не содержат радикалов и трансцендентных функций, т.е. это алгебраические выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Почему неравенства не решают так же, как уравнения?
Итак, нужно найти корни уравнения. Что можно сделать?
Вариант первый.
Зафиксировать область допустимых значений (ОДЗ) выражения: \( x-1 \ne 0; \; x+5 \ne 0. \)
Убедиться в том, что уравнение представляет собой равенство двух дробей и воспользоваться основным свойтвом пропорции — произведение крайних членов пропорции равно произведению её средних членов — в простореции «перемножить крест накрест.» \[(x — 2)\cdot(x+5) = (x-1)\cdot(2x-2).\] Решить простое (без дробей) рациональное уравнение. Здесь после раскрытия скобок и приведения подобных членов оно сведется к квадратному.
Сверить полученные корни с ОДЗ и, отбросив лишние, сформировать ответ.
Вариант второй.
Привести к общему знаменателю. При этом неважно перенесены ли предварительно все члены уравнения в одну сторону или нет.
Не забыть об ограниченности области допустимых значений выражения (написать ОДЗ).
Отбросить общий знаменатель (одинаковые знаменатели в обеих частях равенства, если не переносили всё в одну сторону).
Решить упрощенное уравнение, проверить полученные корни на соответствие ОДЗ, написать ответ.
Вариант третий.
Перенести все члены уравнения в левую часть равенства и привести к общему знаменателю. \[ \frac
Попробуйте всё это проделать самостоятельно для тренировки навыков решения дробно-рациональных уравнений. И убедитесь в том, что во всех трёх случаях будут получены одинаковые ответы.
Для решения уравнений реального ЕГЭ вы можете выбрать любой из этих подходов, который вам придётся по душе.
Здесь дорешаем уравнение в третьем варианте, чтобы потом сравнить его корни с решением неравенства. \[ \left\< <\begin
Ответ: x ∈ <3;4>.
Замечение:Отдельные ответы удобно записывать в фигурных скобках как элементы перечислимого множества, в отличие от интервалов (a;b) и отрезков [a;b], для обозначения которых используются круглые или квадратные скобки соответственно..
Это неравенство содержит те же самые дробные выражения, что и предыдущее уравнение. Однако теперь
варианты «крест накрест» и отбрасывание общего знаменателя НЕПРИМЕНИМЫ,
потому что в знаменателе присутствуют неизвестные величины, а следовательно мы не знаем знаков множителей и не сможем корректно применять свойства неравенств. Особенно это касается свойства 5, которое требует изменить знак неравенства при умножении на отрицательное число. Поэтому при решении дробно-рационального неравенства
самое разумное действие — перенести все его члены в одну сторону и сравнивать итоговое выражение с нулем,
т.е. применим способ аналогичный рассмотренному варианту 3 для уравнений.
Итак, переносим всё в левую часть неравенства и преобразуем выражение: \[ \frac
Далее можем рассуждать так:
Фактически, здесь мы должны определить знак дробного выражения. То есть при каких значениях переменной результат деления является неположительным числом (отрицательным или нулём).
Очевидно, это будет тогда, когда знаки числителя и знаменателя не совпадают. Таким образом, нужно рассмотреть два случая: числитель дроби меньше либо равен нулю И знаменатель положителен (> 0) ИЛИ числитель дроби больше либо равен нулю И знаменатель отрицателен ( 0;> \hfill \\ \end
Объединяя эти случаи, т.е. первую часть ответа с пустым множеством, в итоге получаем:
Ответ: x ∈ (−∞;−5)U(1;3]U[4;+∞) .
Сравним ответ неравенства с ответом уравнения, рассмотренного выше. Значения переменной \(x = -5; x = 1; x = 3; x = 4 \) присутствовали как ключевые при решении уравнения, однако те из них, которые обращают знаменатель в 0, не вошли в ответ.
Но в ответе неравенства мы явно видим все эти значения переменной. Они фигурируют как границы промежутков. При этом входят или не входят граничные точки в ответ зависит от ОДЗ выражений и степени строгости неравенства.
Таким образом, наиболее частые ошибки при решении неравенств состоят в потере граничных точек и слиянии промежутков.
Как проверить ответ неравенства?
И всё-таки, если это ответственное решение, например, важный экзамен, имеет смысл потратить некоторое время и провести вычисление нескольких числовых значений для неравенства.
1) Подставить в неравенство хотя бы по одному значению из промежутков, входящих в ответ, чтобы убедиться, что полученные числовые неравенства будут верными,
2) и по одному значению из промежутков, не входящих в ответ, чтобы убедиться что соответствующие числовые неравенства будут неверными.
3) Также не мешает перепроверить граничные точки промежутков.
Проверка ответа примера 2.
1) Все следующие числовые неравенства должны оказаться верными.
\(x \in (-\infty;-5) \). Пусть \(x = -7 \), тогда \[ \frac<-7-2> <-7-1>\le \frac<-14-2><-7+5>;\;\; \frac<9> <8>0,\) которое является составной частью рассмотренной в примере 2 совокупности систем, будет верным, если оба сомножителя имеют одинаковые знаки — оба положительны или оба отрицательны, т.е. в свою очередь сводится к совокупности двух систем неравенств
Выход из положения может быть следующим:
Если \(7x-7 > 0\), то знак исходного неравенства сохраняется: \[\frac<21> <7x-7>> \frac<8x-8> <7x-7>\Leftrightarrow 21 > 8x-8. \] Если \(7x-7 \frac<8x-8> <7x-7>\Leftrightarrow 21 \frac<8x-8> <7x-7>\Leftrightarrow \left[ <\begin
Вывод: Отбрасывание общего знаменателя можно производить только для тех неравенств, в которых этот знаменатель положительная константа. Т.е. здесь для неравенства (1). Во всех остальных случаях требуется более детальный анализ знаков чисел и выражений.
Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.
Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.
Источник
Как решать дробные уравнения?
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.
Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)
Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1. Дроби и действия с дробями и дробными выражениями.
3. Решение линейных и квадратных уравнений.
Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т.д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)
Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.
В общем, вы поняли.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
А его (надеюсь) уже решит каждый:
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».
А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.
А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)
Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)
А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х 2 +2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
Отлично. Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).
Вот на х(х+2) и умножаем:
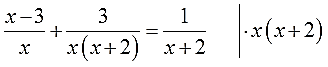
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
И снова получили квадратное уравнение.) Решаем и получаем два корня:
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Ну что, порешаем?)
Ответы (как обычно, вразброс):
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…
Источник