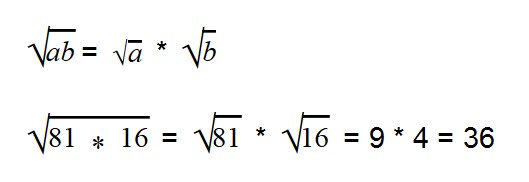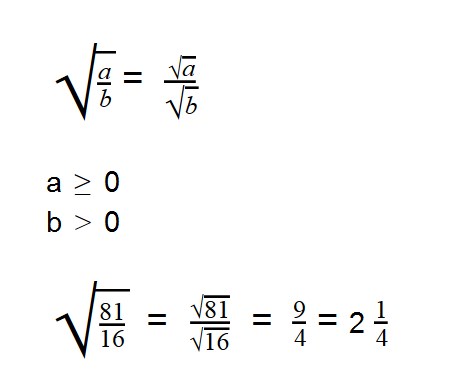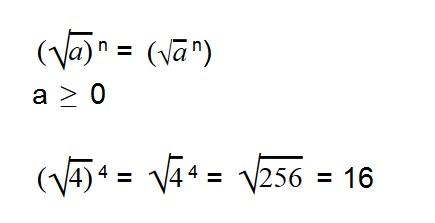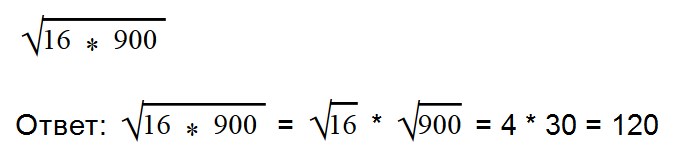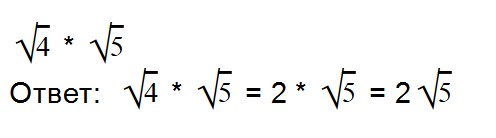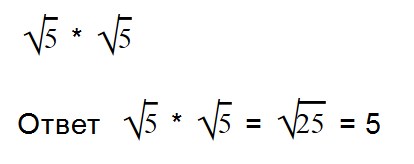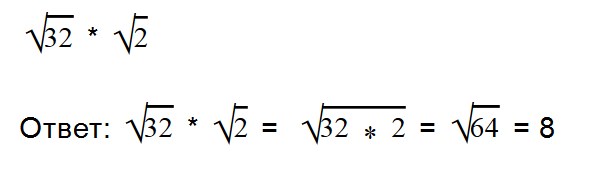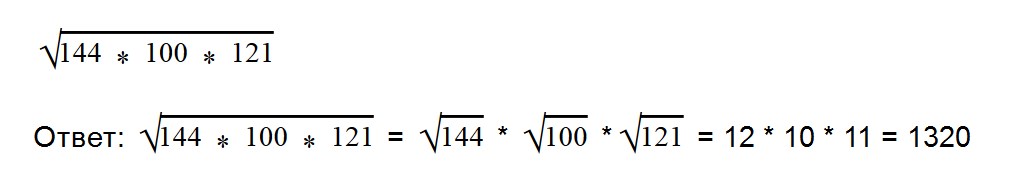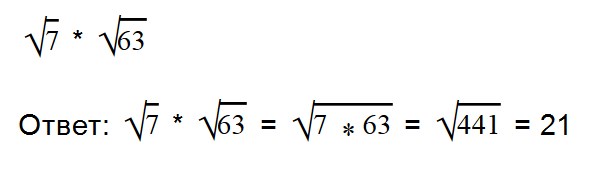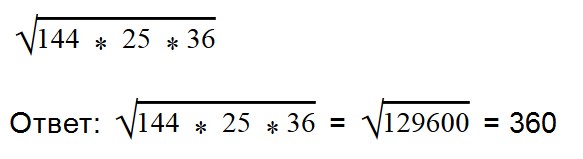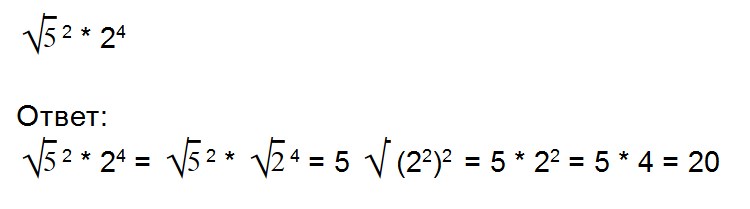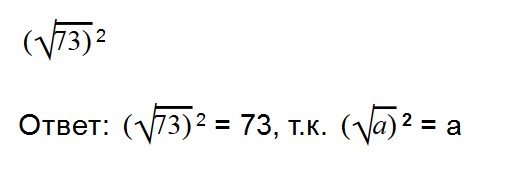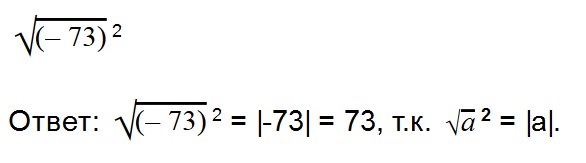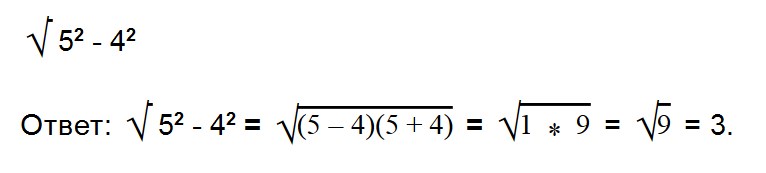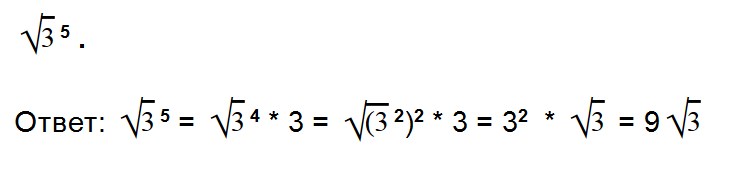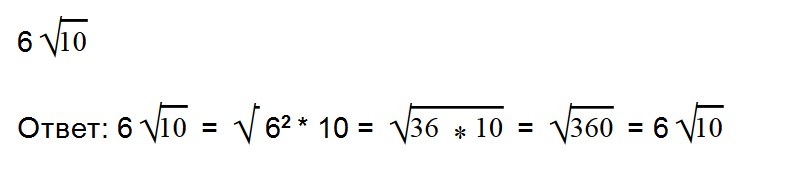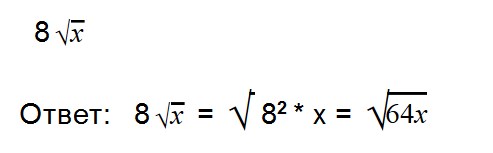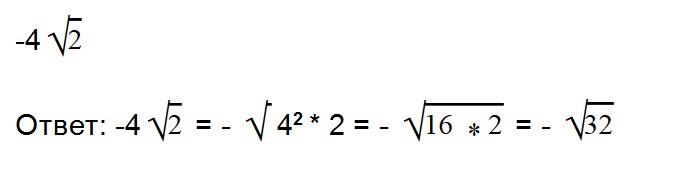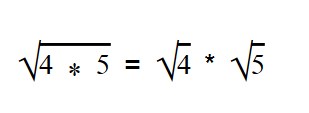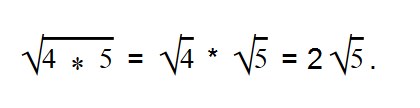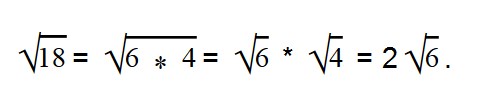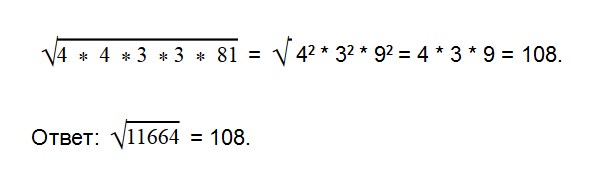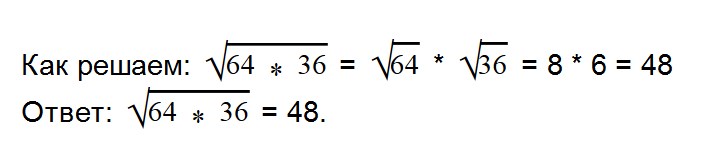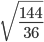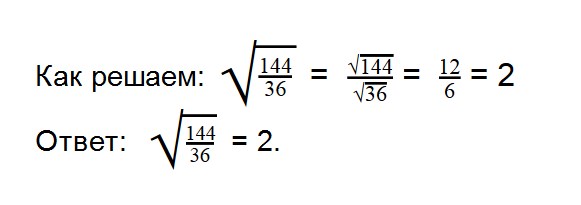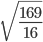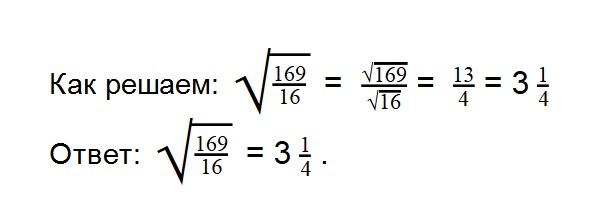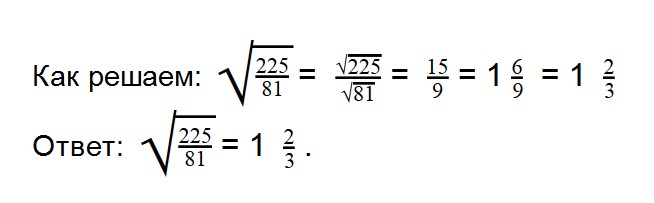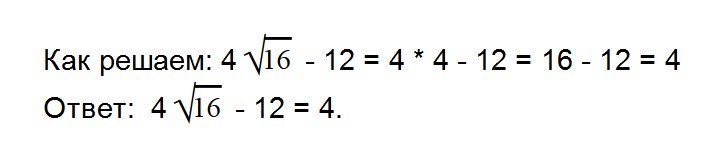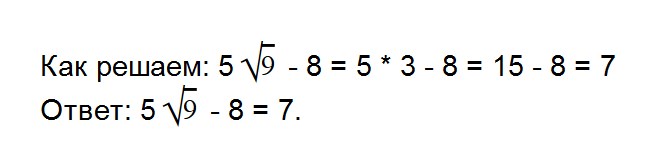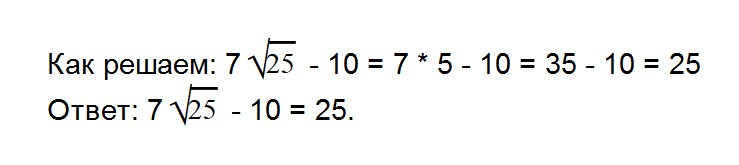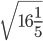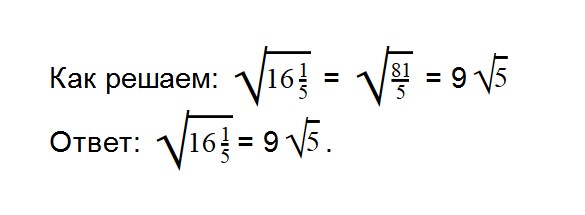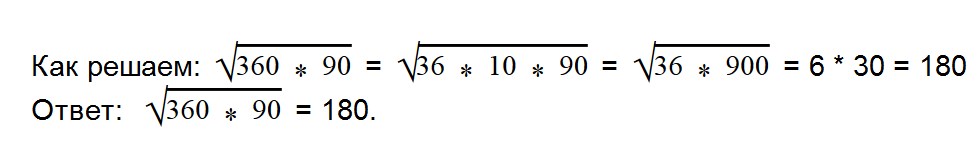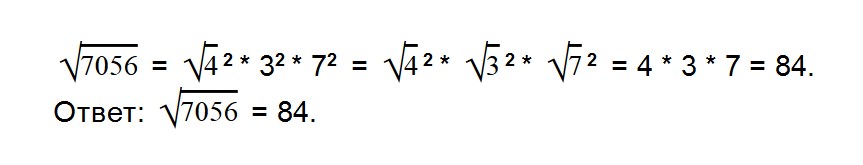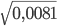Корень под корнем как избавиться

Как вынести из-под корня

Вынесение множителя из-под знака корня — это извлечение корня из одного из множителей (числа или буквы), которые находятся под корнем.

Говорят: «Число « 25 » вынесли из-под знака корня».

Рассмотрим подробнее пример вынесения множителя из-под знака корня.

№ 15 .1 (в) Мордкович 8 класс

Вынесите множитель из-под знака корня:

Извлечь квадратный корень из « √ 5 » целым числом не получится, поэтому нам остается только извлечь квадратный корень из « √ 16 ».

Обязательно выучите таблицу квадратов чисел от « 1 » до « 15 » и таблицу часто используемых квадратных корней.

Вспомним, чему равен квадрат числа четыре?

Решение примера выше записываем следующим образом.

√ 16 · 5 = √ 16 · √ 5 = 4 · √ 5

Действие выше называют вынесением множителя из-под знака корня. Говорят: «Число « 16 » вынесли из-под знака корня, получив число « 4 ».

Выносить из-под знака корня можно, только если все действия под знаком корня — умножение .

Примеры правильного и неправильного вынесения из-под знака корня:

• √ 144 · 2 = √ 144 · √ 2 = 12 √ 2 (верно) . Под знаком квадратного корня только действие умножения;
• √ 16 + 5 ≠ 4 + √ 5 (неверно) . Нельзя выносить « 16 » из-под знака корня, так как под знаком корня сложение ;
• √ 25 − 3 ≠ 5 − √ 3 (неверно) . Нельзя выносить из-под знака корня « 25 », так как под знаком корня вычитание ;
• √ 16 ·2 + 3 ≠ 4 √ 2 + 3 (неверно) . Нельзя выносить « 16 » из-под знака корня, так как под знаком корня есть сложение (должно быть только умножение ).

Как вынести множитель из корня с одним числом

Рассмотрим пример, когда под корнем только одно число и по условию задания требуется вынести множитель из-под знака корня.

№ 524 (1) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

Извлечь целое число из квадратного корня « √ 8 » нельзя, так как нет такого целого числа, которое в квадрате давало бы « 8 ».

Обязательно выучите таблицу квадратов чисел от « 1 » до « 15 » и таблицу часто используемых квадратных корней.

Подумаем, на какие множители можно разложить число « 8 », чтобы была возможность вынести один из множителей из-под знака корня. Вспоминаем таблицу умножения.

Число « 8 » — это произведение
« 8 = 4 · 2 ». Теперь можем вынести « 4 » из-под знака корня.

√ 8 = √ 4 · 2 = √ 4 · √ 2 = 2 √ 2

Разберем другие примеры вынесения множителя из-под знака квадратного корня

№ 524 (4) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

Зададим себе вопрос: «На какие множители нужно разложить « 54 », чтобы была возможность вынести один из множителей из-под знака квадратного корня?».

Видим число « 9 ». Подходит, так как « √ 9 = 3 ».

Завершим решение примера вынесением из-под знака корня числа « 9 ».

√ 54 = √ 9 · 6 = 3 √ 6

Извлечь « √ 6 » целым числом невозможно. Поэтому ответ оставляем в таком виде.

№ 524 (5) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

В примерах с числами, которые делятся на « 10, 100, 1000… » и так далее, стоит сразу попробовать разложить число на « 10, 100, 1000… » и второй множитель.

То есть число « 490 » можно разложить на « 490 = 49 · 10 ». Из « 49 » можно извлечь квадратный корень.

Теперь можно вынести « 49 » из-под знака корня.

√ 490 = √ 49 · 10 = 7 √ 10

№ 524 (6) Мерзляк 8 класс

№ 524 (8) Мерзляк 8 класс

√ 108 = √ 54 · 2 = √ 9 · 6 · 2 =

= 3 √ 6 · 2 = 3 √ 12 = 3 √ 4 · 3 =

№ 526 (6) Мерзляк 8 класс

0,4 · √ 250 = 0,4 · √ 25 · 10 =

Завершим пример, умножив десятичную дробь « 0,4 » на « 5 » по правилу умножения десятичной дроби на число.

0,4 · √ 250 = 0,4 · √ 25 · 10 =

= 0,4 · 5 √ 10 = 2 √ 10

№ 526 (8) Мерзляк 8 класс

4

9

· √ 63 =

4

9

· √ 9 · 7 =

4

9

· 3 √ 7 = …
Умножим дробь «

4

9

» на число « 3 », которое вынесли из-под знака квадратного корня. Используем правило умножения обыкновенной дроби на число.

4

9

· √ 63 =

4

9

· √ 9 · 7 =

4

9

· 3 √ 7 =

=

4 · 3

9

· √ 7 =

4 · 3

9 3

· √ 7 =

=

4

3

· √ 7 = …

Чтобы дать окончательный ответ, выделим целую часть неправильной дроби «

4

3

».

4

9

· √ 63 =

4

9

· √ 9 · 7 =

4

9

· 3 √ 7 =

=

4 · 3

9

· √ 7 =

4 · 3

9 3

· √ 7 =

4

3

· √ 7 =

= 1

1

3

· √ 7

Как вынести десятичную дробь из-под знака корня

В уроке «Как извлечь квадратный корень из дроби» мы разбирали, каким образом извлечь квадратный корень из десятичной дроби. Например, извлечение квадратного корня из десятичной дроби « √ 0,25 ».

√ 0,25 = 0,5 , так как
0,5 2 = 0,5 · 0,5 = 0,25

Тот же самый метод используется при вынесении десятичной дроби из-под знака корня.

№ 524 (10) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

Разложим десятичную дробь на произведение множителей, чтобы потом была возможность вынести один из множителей из-под знака корня.

Подберем десятичную дробь, на которую делится « 0,48 », из которой потом можно извлечь квадратный корень.

Например, « 0,16 ». Десятичная дробь « 0,48 » делится на « 0,16 » нацело.

Извлечь квадратный корень из « √ 0,16 » по правилу нахождения квадратного корня из десятичной дроби.

Завершим пример вынесением « 0,16 » из-под знака корня.

Примеры вынесения десятичной дроби из-под знака квадратного корня

№ 524 (9) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

№ 526 (7) Мерзляк 8 класс

Вынесите множитель из-под знака корня:

−2 · √ 0,18 = −2 · √ 0,09 · 2 =

= −2 · 0,3 √ 2 = −0,6 √ 2

Как вынести букву из-под знака корня

При вынесении из-под знака квадратного корня множителя в степени (буквы или числа) степень делится на « 2 ».

• √ a 2 = a
  

  2

  2

  = a 1 = a , гдe a ≥ 0

• √ y 4 = y
  

  4

  2

  = y 2 , гдe y ≥ 0

• √ 12 4 = 12
  

  4

  2

  = 12 2 = 144

• √ x 6 = x
  

  6

  2

  = x 3 , гдe x ≥ 0

Рассмотрим примеры вынесения буквы в степени из-под корня.

№ 347 (2, 4) Колягин (Алимов) 8 класс

Вынести множитель из-под знака корня (буквами обозначены положительные числа).

2) √ 2x 2 = x

2

2

√ 2 = x √ 2

4) √ 3a 6 = a

6

2

√ 3 = a 3 √ 3

В более сложных примерах требуется вынести и числовой множитель, и букву в степени из-под корня.

№ 348 (2) Колягин (Алимов) 8 класс

Вынести множитель из-под знака корня (буквами обозначены положительные числа).

Вначале отдельно вынесем буквенный множитель из-под корня.

√ 75a 2 = a

2

2

· √ 75 = a √ 75 = …

Теперь разложим число « 75 » на множители, один из которых можно вынести из-под знака квадратного корня.

Число « 75 » явно делится на « 5 ». Проверим, можно ли число « 75 » разложить на квадрат числа « 5 2 = 25 ».

Завершим пример, вынеся число « 25 » из-под знака корня.

√ 75a 2 = a

2

2

· √ 75 = a √ 75 =

= a √ 25 · 3 = 5a √ 3

№ 549 (2) Мерзляк 8 класс

Не всегда удается сразу вынести букву в степени из-под знака корня. В данном примере степень « 9 » не делится нацело на « 2 ».

Вспомним из урока «Свойства степени» правило произведение степеней с одинаковым основанием.

Свойство работает и в обратную сторону.

Вернемся к нашему примеру. Разложим « y 9 » на множители со степенями так, чтобы одна из степеней нацело делилась на « 2 ». Представим степень « 9 » как сумму чисел « 9 = 6 + 3 ».

Используем свойство произведения степеней с одинаковым основанием в обратную сторону и разложим « у » на множители.

Источник

Что такое квадратный корень

О чем эта статья:

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Здесь могут возникнуть резонные вопросы, почему, например, в примере x 2 = 16, x = 4 и x = -4.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

• x 2 = 16 не равно x = √16.

Это два нетождественных друг другу выражения.

• x 2 = 16 — это квадратное уравнение.
• x = √ 16 — арифметический квадратный корень.

Из выражения x 2 = 16 следует, что:

• |x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

1. Пример решен неверно
2. Это квадратное уравнение.

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Решение следующее:
Строим график функции y = x 2 .
Отмечаем решения на графике: -√2; √2.

Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: √2 = 1,414213… .

В таком виде ответ не записывают — нужно оставить квадратный корень.
x 2 = 2.
x = √2
x = -√2.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

• 1. Извлеките квадратный корень: √289

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Влево — 1, вверх — 7.

• 2. Извлеките квадратный корень: √3025

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

• 3. Извлеките квадратный корень: √7396

Ищем в таблице число 7396.

Влево — 8, вверх — 6.

• 4. Извлеките корень: √9025

Ищем в таблице число 9025.

Влево — 9, вверх — 5.

• 5. Извлеките корень √1600

Ищем в таблице число 1600.

Влево — 4, вверх — 0.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

• Корень произведения равен произведению корней
  
• Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
  
• Чтобы возвести корень в степень, нужно возвести в степень значение под корнем
  

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

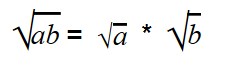Примеры:

1. 
2. 

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

1. 
2. 
3. Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:
   

1. 
2. 

Деление арифметических корней

Для деления арифметических корней используйте формулу:

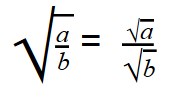Примеры:

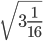
Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49

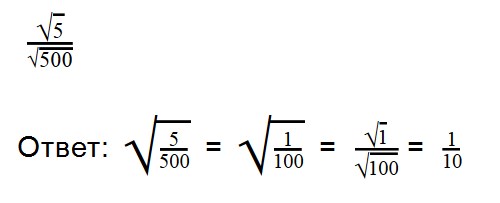
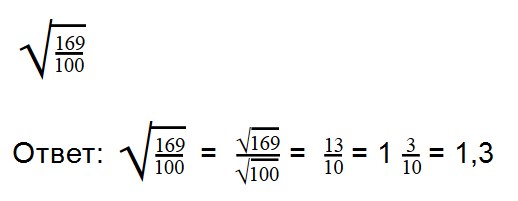
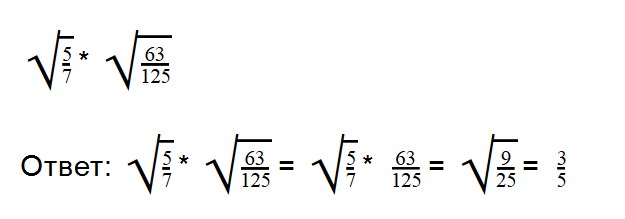
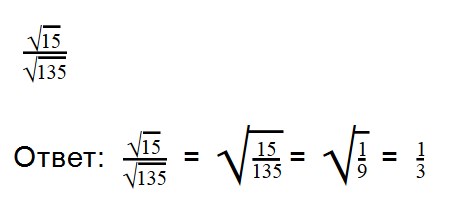
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

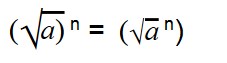Примеры:

1. 
2. 
3. 

Эти две формулы нужно запомнить:

• (√a) 2 = a
• √a 2 = |a|

1. 
2. 

Повторите свойства степеней, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Дано выражение: 7√9

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

1. 
2. 
3. 

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.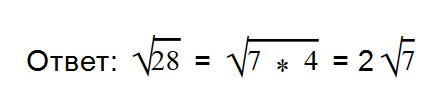

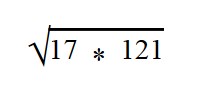
Ответ: по правилу извлечения квадратного корня из произведения,

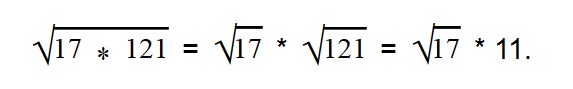
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.

Вынесите множитель из-под знака корня в выражении: √24

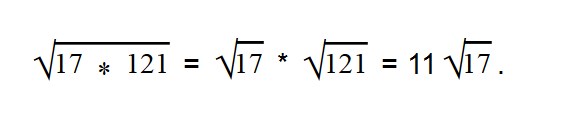
Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.

Упростите выражение:

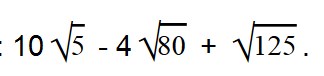
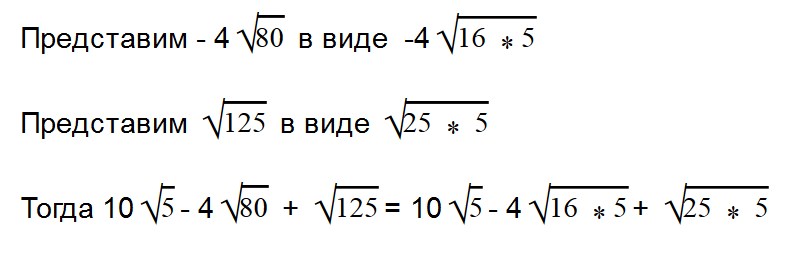
Вынесем в двух последних выражения множитель из-под знака корня.

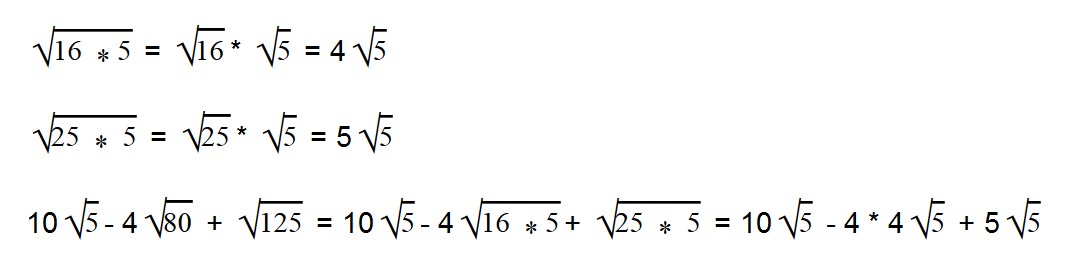
Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.

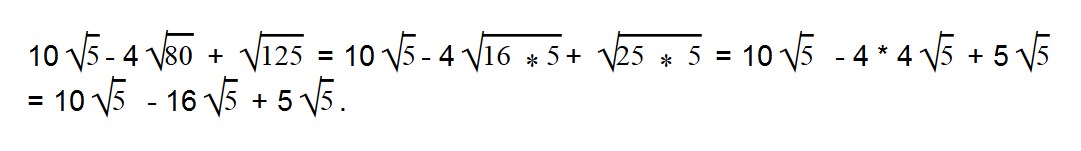
Мы видим, что во всем выражении есть один общий множитель — √5.
Выносим общий множитель за скобки:

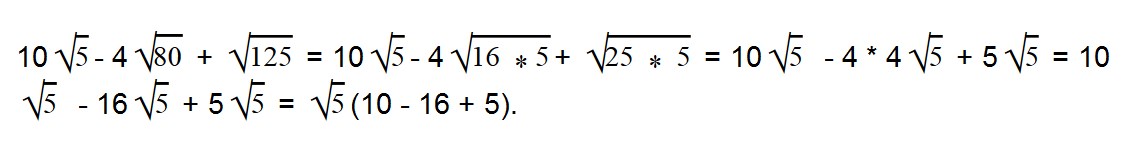
Далее вычисляем все, что в скобках:

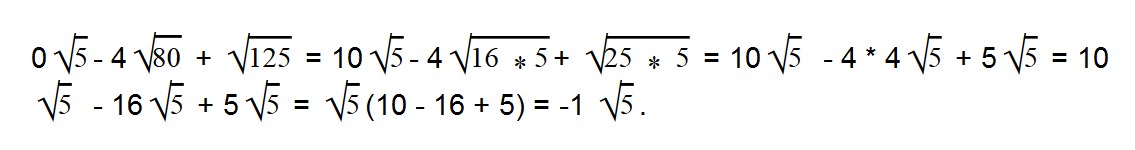
Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Сравните два выражения: √50 и 9√5

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Это значит, что 6√5 > √18.

Сравните два выражения: 7√12 и √20

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

1. Определить «сотни», между которыми оно стоит.
2. Определить «десятки», между которыми оно стоит.
3. Определить последнюю цифру в этом числе.

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

Это значит, что число 2116 находится между 40 2 и 50 2 .

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Таким образом, у нас остаются два варианта: 44 2 и 46 2 .

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

• 1. Вычислите значение квадратного корня: √36
  
• 2. Вычислите значение квадратного корня: √64*36
  
• 3. Вычислите значение квадратного корня:
  
• 4. Вычислите значение квадратного корня:
  
• 5. Вычислите значение квадратного корня:
  
• 6. Вычислите значение выражения: 4√16 — 12
  
• 7. Вычислите значение выражения: 5√9 — 8
  
• 8. Вычислите значение выражения: 7√25 — 10
  
• 9. Вычислите значение квадратного корня:
  
• 10. Вычислите значение квадратного уравнения:
  
• 11. Вычислите значение квадратного уравнения:
  
• 12. Извлеките квадратный корень из числа √7056 удобным вам способом
  Как решаем:
  

  

• 13. Вычислите значение квадратного корня √0,81
  Ответ: √0,81 = 0,9
• 14. Вычислите значение квадратного корня:
  Как решаем: = 0,09
• 15. Вычислите значение выражения: 8√81 — 20
  Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
  Ответ: 8√81 — 20 = 52.
• 16. Вычислите значение выражения: 13√100 — 15
  Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
  Ответ: 13√100 — 15 = 115.
• 17. Вычислите значение выражения: √16 + 5√4
  Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24.
• 18. Вычислите значение выражения: √36 + 2√9
  Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
  Ответ: √36 + 2√9 = 12.
• 19. Вычислите значение выражения: 2√16 — 3√25
  Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
  Ответ: 2√16 — 3√25 = -7.
• 20. Вычислите значение выражения: 3√81 — 5√9
  Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
  Ответ: 3√81 — 5√9 = 12.
• 21. Вынесите множитель из-под знака корень: √60
  Как решаем: √60 = √15 * √4 = 2√15
  Ответ: √60 = 2√15.
• 22. Вынесите множитель из-под знака корень: √160
  Как решаем: √160 = √16 * √10 = 4√10
  Ответ: √160 = 4√10.
• 23. Внесите множитель под знак корня: 6√7
  Как решаем: √6 2 * 7 = √36 * √7 = √252
  Ответ: 6√7 = √252.
• 24. Внесите множитель под знак корня: 8√2
  Как решаем: 8√2 = √8 2 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128.
• 25. Внесите множитель под знак корня: 9√5

  Как решаем: 9√5 = √9 2 * 5 = √81 * √5 = √405
  Ответ: 9√5 = √405.

• 26. Упростите выражение: (5 — √2) 2
  Как решаем: (5 — √2) 2 = 5 2 — 2 * 5 * √2 + (√2) 2 = 25 — 10√2 + 2 = 27 — 10√2.
  Ответ: (5 — √2) 2 = 27 — 10√2.
• 27. Вычислите значение выражения: 3√49 — 3√25
  Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
  Ответ: 3√49 — 3√25 = 6.
• 28. Вычислите значение квадратного корня: √484 * √576
  Как решаем: √484 * √576 = 22 * 24 = 528
  Ответ: √484 * √576 = 528.
• 29. Вычислите значение квадратного корня: √625 * √81
  Как решаем: √625 * √81 = 25 * 9 = 225
  Ответ: √625 * √81 = 225.
• 30. Найдите значение выражения: 3√100 — √144
  Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
  Ответ: 3√100 — √144 = 18.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник