Ваш IP заблокирован
Убедитесь, что Вы не используете анонимайзеры/прокси/VPN или другие подобные средства (TOR, friGate, ZenMate и т.п.) для доступа к сайту.
Отправьте письмо на abuse[at]twirpx.club если Вы уверены, что эта блокировка ошибочна.
В письме укажите следующие сведения о блокировке:
Кроме того, пожалуйста, уточните:
- Каким Интернет-провайдером Вы пользуетесь?
- Какие плагины установлены в Вашем браузере?
- Проявляется ли проблема если отключить все плагины?
- Проявляется ли проблема в другим браузере?
- Какое программное обеспечение для организации VPN/прокси/анонимизации Вы обычно используете? Проявляется ли проблема если их отключить?
- Давно ли в последний раз проверяли компьютер на вирусы?
Your IP is blocked
Ensure that you do not use anonymizers/proxy/VPN or similar tools (TOR, friGate, ZenMate etc.) to access the website.
Contact abuse[at]twirpx.club if you sure this block is a mistake.
Attach following text in your email:
Please specify also:
- What Internet provider (ISP) do you use?
- What plugins and addons are installed to your browser?
- Is it still blocking if you disable all plugins installed to your browser?
- Is it still blocking if you use another browser?
- What software do you often use for VPN/proxy/anonymization? Is it still blocking if you disable it?
- How long ago have you checked your computer for viruses?
Источник
ПОСЛЕДОВАТЕЛЬНОСТЬ ОФОРМЛЕНИЯ РАБОТЫ



МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА»
________________________________________________________________
Кафедра «Машиноведение, проектирование,
Стандартизация и сертификация»
С.Н. МУРАВЬЕВ, Н.А. ЧВАНОВА
ПРЕОБРАЗОВАНИЕ ЭПЮРА ПРИ ОПРЕДЕЛНИИ РАЗМЕРОВ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
Учебно-методическое пособие
МОСКВА – 2020
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА»
______________________________________________________________________
Кафедра «Машиноведение, проектирование,
Стандартизация и сертификация»
ПРЕОБРАЗОВАНИЕ ЭПЮРА ПРИ ОПРЕДЕЛНИИ РАЗМЕРОВ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
Учебно-методическое пособие
Для выполнения графической работы по дисциплине
«Начертательная геометрия и компьютерная графика»
для студентов ИТТСУ, ИУИТ и Вечернего факультета
МОСКВА – 2020
Муравьев С.Н., Чванова Н.А. Преобразование эпюра при определении размеров плоских геометрических фигур: Учебно-методическое пособие для выполнения графической работы по дисциплине «Начертательная геометрия и компьютерная графика». – М.: РУТ (МИИТ), 2020. – 32 с.: ил.
Предлагаемое учебно-методическое пособие содержит сжатое изложение основных понятий и определений, которые необходимо знать обучающимся при решении задач на определение размеров плоских геометрических фигур способом замены плоскостей проекций.
Объём предлагаемого материала позволяет самостоятельно установить размеры плоских геометрических фигур, заданных в разделе 6 «ТАБЛИЦА ОПРЕДЕЛИТЕЛЕЙ».
Издание предназначено для обучающихся, изучающих разделы «Точка, прямая, плоскость» и «Способы преобразования эпюра» курса «Начертательная геометрия».
Ил. 18, табл. 2, библиогр. – 2 назв.
Рецензент: заведующий кафедрой «Электропоезда и локомотивы» РУТ (МИИТ), д.т.н. Пудовиков О.Е.
СОДЕРЖАНИЕ
1. СОДЕРЖАНИЕ РАБОТЫ …. …………….…. …… 4
2. ПОСЛЕДОВАТЕЛЬНОСТЬ ОФОРМЛЕНИЯ РАБОТЫ …….. 5
ПОСТРОЕНИЕ ПРОЕКЦИЙ ПЛОСКОГО
МНОГОУГОЛЬНИКА ПО ЗАДАННЫМ УСЛОВИЯМ
(ЗАДАЧА № 1) ………………………. ……………………. 10
ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ЗАДАННОЙ ТОЧКИ
ДО ПЛОСКОСКОГО МНОГОУГОЛЬНИКА (ЗАДАЧА № 2) . 13
ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ПЛОСКОГО
МНОГОУГОЛЬНИКА (ЗАДАЧА № 3) …………………………. 20
6. ТАБЛИЦА ОПРЕДЕЛИТЕЛЕЙ ………………………………….. 22
СПИСОК ЛИТЕРАТУРЫ ……………………………………. … 30
ВВЕДЕНИЕ
Настоящее учебно-методическое пособие предназначено в помощь обучающимся для выполнения графической работы «Точка, прямая, плоскость» (далее – Работа).
Работа выполняется на основе теоретических положений, изложенных в разделах «Точка, прямая, плоскость» и «Способы преобразования эпюра» курса «Начертательная геометрия».
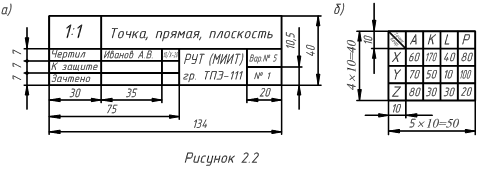
При оформлении Работы необходимо строго соблюдать требования, предъявляемые Единой системой конструкторской документации (далее – ЕСКД) в части расположения проекций, структуры линий, форм и мест расположения надписей на листах формата.
Заданием на указанную Работу служит один из 64-х предлагаемых в таблице определителей вариантов задания. Каждый вариант содержит три задачи.
СОДЕРЖАНИЕ РАБОТЫ
Работа включает в себя метрические, позиционные и конструктивные задачи, связанные с построением проекций геометрических фигур, отвечающих заданным условиям. Каждому обучающемуся необходимо выполнить следующие три задачи:

Задача № 1. Построить проекции плоского многоугольника по заданным условиям.
Задача № 2. Построить проекции расстояния от заданной точки до плоского многоугольника.
Задача № 3. Определить размеры (натуральную величину) плоского многоугольника.
Особое внимание следует обратить на то, что вид плоского многоугольника, который необходимо построить при решении задачи № 1, зависит от номера варианта индивидуального задания.
Виды плоских многоугольников определяются номерами варианта индивидуального задания:
Варианты заданий 1 ÷ 8. Построить проекции параллелограмма ABCD, если диагональ AC перпендикулярна прямой KL, а сторона DC принадлежит прямой KL и равна AC.
Варианты заданий 9 ÷ 16. Построить проекции квадрата ABCD, если его диагональ BD принадлежит прямой KL.
Варианты заданий 17 ÷ 24. Построить проекции равнобочной трапеции ABCD, высота которой равна меньшему основанию, а большее основание DC принадлежит прямой KL и равно 3│AB│.
Варианты заданий 25 ÷ 32. Построить проекции ромба ABCD, диагональ BD которого принадлежит прямой KL, а отношение диагоналей AC : BD = 1 : 2.
Варианты заданий 33 ÷ 64. Построить проекции равнобедренного прямоугольного треугольника ABC, катет BC которого принадлежит прямой KL.
Для всех условий задачи исходными данными являются точка A и прямая KL.
ПОСЛЕДОВАТЕЛЬНОСТЬ ОФОРМЛЕНИЯ РАБОТЫ
Работа выполняется обучающимися самостоятельно, а вопросы, возникающие в процессе её выполнения, следует выяснять у преподавателя в часы практических занятий или в часы консультаций.
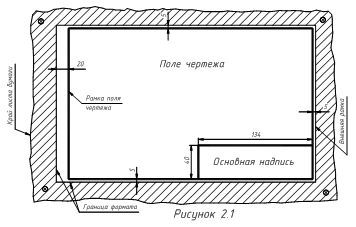
Работа должна быть выполнена на листе формата А3 (297´420 мм) с применением простых карандашей соответствующей твёрдости. Результат решения задачи рекомендуется выделить сплошной толстой основной линией. Толщина линии проекционной связи »1/3 от толщины сплошной основной линии.
Последовательность выполнения Работы:
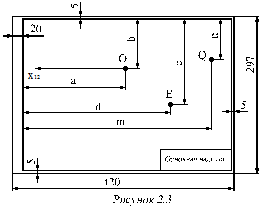
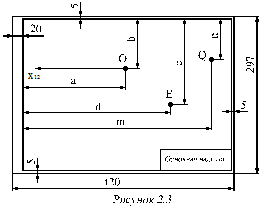
для рационального расположения проекций плоского многоугольника на листе формата точку E (задача № 2) следует располагать с учётом значений величин отрезков d и c (см. рисунок 2.3), приведённых в таблице 2.1, в соответствии с номером варианта индивидуального задания;
для рационального расположения проекций плоского многоугольника на листе формата точку Q (задача № 3) следует располагать с учётом значений величин отрезков m и n (см. рисунок 2.3), приведённых в таблице 2.1, в соответствии с номером варианта индивидуального задания.
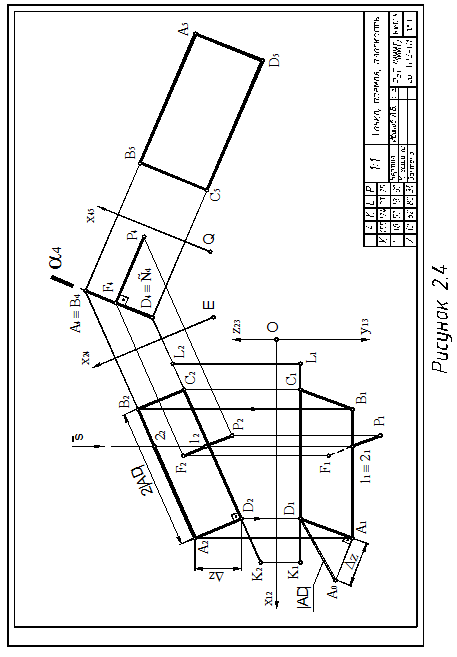
Пример оформления графической работы «Точка, прямая, плоскость» приведён на рисунке 2.4.
Источник
ПОСЛЕДОВАТЕЛЬНОСТЬ ОФОРМЛЕНИЯ РАБОТЫ
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА»
________________________________________________________________
Кафедра «Машиноведение, проектирование,
Стандартизация и сертификация»
С.Н. МУРАВЬЕВ, Н.А. ЧВАНОВА
ПРЕОБРАЗОВАНИЕ ЭПЮРА ПРИ ОПРЕДЕЛНИИ РАЗМЕРОВ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
Учебно-методическое пособие
МОСКВА – 2020
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА»
______________________________________________________________________
Кафедра «Машиноведение, проектирование,
Стандартизация и сертификация»
ПРЕОБРАЗОВАНИЕ ЭПЮРА ПРИ ОПРЕДЕЛНИИ РАЗМЕРОВ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
Учебно-методическое пособие
Для выполнения графической работы по дисциплине
«Начертательная геометрия и компьютерная графика»
для студентов ИТТСУ, ИУИТ и Вечернего факультета
МОСКВА – 2020
Муравьев С.Н., Чванова Н.А. Преобразование эпюра при определении размеров плоских геометрических фигур: Учебно-методическое пособие для выполнения графической работы по дисциплине «Начертательная геометрия и компьютерная графика». – М.: РУТ (МИИТ), 2020. – 32 с.: ил.
Предлагаемое учебно-методическое пособие содержит сжатое изложение основных понятий и определений, которые необходимо знать обучающимся при решении задач на определение размеров плоских геометрических фигур способом замены плоскостей проекций.
Объём предлагаемого материала позволяет самостоятельно установить размеры плоских геометрических фигур, заданных в разделе 6 «ТАБЛИЦА ОПРЕДЕЛИТЕЛЕЙ».
Издание предназначено для обучающихся, изучающих разделы «Точка, прямая, плоскость» и «Способы преобразования эпюра» курса «Начертательная геометрия».
Ил. 18, табл. 2, библиогр. – 2 назв.
Рецензент: заведующий кафедрой «Электропоезда и локомотивы» РУТ (МИИТ), д.т.н. Пудовиков О.Е.
СОДЕРЖАНИЕ
1. СОДЕРЖАНИЕ РАБОТЫ …. …………….…. …… 4
2. ПОСЛЕДОВАТЕЛЬНОСТЬ ОФОРМЛЕНИЯ РАБОТЫ …….. 5
ПОСТРОЕНИЕ ПРОЕКЦИЙ ПЛОСКОГО
МНОГОУГОЛЬНИКА ПО ЗАДАННЫМ УСЛОВИЯМ
(ЗАДАЧА № 1) ………………………. ……………………. 10
ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ЗАДАННОЙ ТОЧКИ
ДО ПЛОСКОСКОГО МНОГОУГОЛЬНИКА (ЗАДАЧА № 2) . 13
ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ПЛОСКОГО
МНОГОУГОЛЬНИКА (ЗАДАЧА № 3) …………………………. 20
6. ТАБЛИЦА ОПРЕДЕЛИТЕЛЕЙ ………………………………….. 22
СПИСОК ЛИТЕРАТУРЫ ……………………………………. … 30
ВВЕДЕНИЕ
Настоящее учебно-методическое пособие предназначено в помощь обучающимся для выполнения графической работы «Точка, прямая, плоскость» (далее – Работа).
Работа выполняется на основе теоретических положений, изложенных в разделах «Точка, прямая, плоскость» и «Способы преобразования эпюра» курса «Начертательная геометрия».
При оформлении Работы необходимо строго соблюдать требования, предъявляемые Единой системой конструкторской документации (далее – ЕСКД) в части расположения проекций, структуры линий, форм и мест расположения надписей на листах формата.
Заданием на указанную Работу служит один из 64-х предлагаемых в таблице определителей вариантов задания. Каждый вариант содержит три задачи.
СОДЕРЖАНИЕ РАБОТЫ
Работа включает в себя метрические, позиционные и конструктивные задачи, связанные с построением проекций геометрических фигур, отвечающих заданным условиям. Каждому обучающемуся необходимо выполнить следующие три задачи:
Задача № 1. Построить проекции плоского многоугольника по заданным условиям.
Задача № 2. Построить проекции расстояния от заданной точки до плоского многоугольника.
Задача № 3. Определить размеры (натуральную величину) плоского многоугольника.
Особое внимание следует обратить на то, что вид плоского многоугольника, который необходимо построить при решении задачи № 1, зависит от номера варианта индивидуального задания.
Виды плоских многоугольников определяются номерами варианта индивидуального задания:
Варианты заданий 1 ÷ 8. Построить проекции параллелограмма ABCD, если диагональ AC перпендикулярна прямой KL, а сторона DC принадлежит прямой KL и равна AC.
Варианты заданий 9 ÷ 16. Построить проекции квадрата ABCD, если его диагональ BD принадлежит прямой KL.
Варианты заданий 17 ÷ 24. Построить проекции равнобочной трапеции ABCD, высота которой равна меньшему основанию, а большее основание DC принадлежит прямой KL и равно 3│AB│.
Варианты заданий 25 ÷ 32. Построить проекции ромба ABCD, диагональ BD которого принадлежит прямой KL, а отношение диагоналей AC : BD = 1 : 2.
Варианты заданий 33 ÷ 64 . Построить проекции равнобедренного прямоугольного треугольника ABC, катет BC которого принадлежит прямой KL.
Для всех условий задачи исходными данными являются точка A и прямая KL.
ПОСЛЕДОВАТЕЛЬНОСТЬ ОФОРМЛЕНИЯ РАБОТЫ
Работа выполняется обучающимися самостоятельно, а вопросы, возникающие в процессе её выполнения, следует выяснять у преподавателя в часы практических занятий или в часы консультаций.
Работа должна быть выполнена на листе формата А3 (297´420 мм) с применением простых карандашей соответствующей твёрдости. Результат решения задачи рекомендуется выделить сплошной толстой основной линией. Толщина линии проекционной связи »1/3 от толщины сплошной основной линии.
Последовательность выполнения Работы:
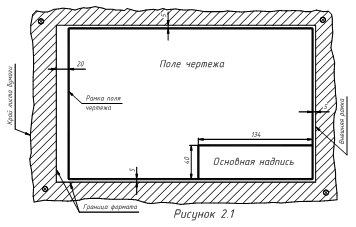
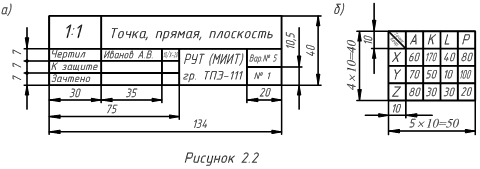
для рационального расположения проекций плоского многоугольника на листе формата точку E (задача № 2) следует располагать с учётом значений величин отрезков d и c (см. рисунок 2.3), приведённых в таблице 2.1, в соответствии с номером варианта индивидуального задания;
для рационального расположения проекций плоского многоугольника на листе формата точку Q (задача № 3) следует располагать с учётом значений величин отрезков m и n (см. рисунок 2.3), приведённых в таблице 2.1, в соответствии с номером варианта индивидуального задания.
Пример оформления графической работы «Точка, прямая, плоскость» приведён на рисунке 2.4.
Точка O
Точка E
Точка Q
Продолжение таблицы 2.1
Точка O
Точка E
Точка Q
Дата добавления: 2020-11-15 ; просмотров: 130 ; Мы поможем в написании вашей работы!
Источник