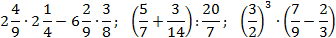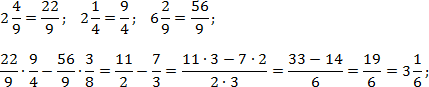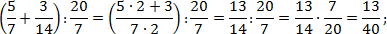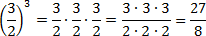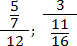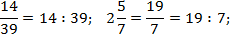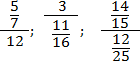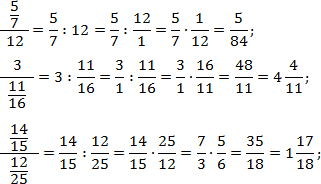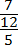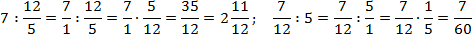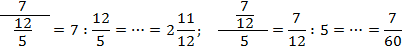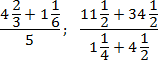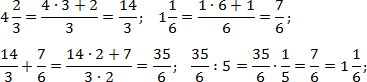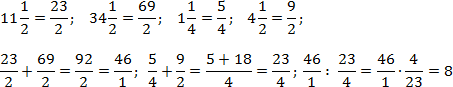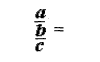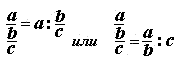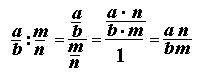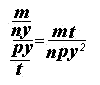Сложные выражения с дробями. Порядок действий
Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?
В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:
- Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
- Затем — деление и умножение;
- Последним шагом выполняется сложение и вычитание.
Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.
Задача. Найдите значения выражений:
Переведем все дроби из первого выражения в неправильные, а затем выполним действия:
Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, . Тогда:
Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, , имеем:
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.
Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:
Многоэтажные дроби
До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.
Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:
Здесь и далее мы будем называть эти дроби . Однако имейте в виду, что общепризнанного названия у них нет, и в разных учебниках могут встречаться другие определения.
Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:
Задача. Переведите многоэтажные дроби в обычные:
В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Получаем:
В последнем примере перед окончательным умножением дроби были сокращены.
Специфика работы с многоэтажными дробями
В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:
Это выражение можно прочитать по-разному:
- В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
- В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.
Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.
Если следовать этому правилу, то приведенные выше дроби надо записать так:
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:
Задача. Найдите значения выражений:
Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили в форме дроби, чтобы выполнить деление.
Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.
Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.
Источник
Трехэтажная дробь как избавиться
Урок Иванчук Н.В., учителя математики лицея № 1 г. Мурманска
Опубликовано: Резник Н.А. Многоэтажные дроби //
Математика в школе, 2002. №7. С. 55-60.
Материал предоставляется для свободного некоммерческого использования
с обязательной ссылкой на авторов (согласно ст. 1229 Гражданского кодекса РФ)
| Тема «Действия с алгебраическими дробями» вызывает у учащихся 7-8 классов определённые трудности, так как требует хороших знаний материала, изученного ранее: «Действия с обыкновенными дробями», «Преобразование многочленов», «Формулы сокращённого умножения». Если предшествующие знания по каким-то причинам сформированы недостаточно прочно, то под наплывом нового материала они как бы растворяются и, как следствие, являются тормозом для дальнейшего успешного обучения. Успешно реализовывать задачу закрепления «старых» и формирования «новых» знаний позволяет визуализация учебного материала. Если учебная информация сопровождается определёнными рисунками, соответствующими формулами, зрительными подсказками, то её смысл становится видимым, понятным и, как следствие, лучше запоминается. Именно поэтому мы обратились к новым учебнику и задачнику для 7-го класса, выпущенных Санкт-Петербургским Институтом Продуктивного обучения Российской Академии Образования [1, 2]. В восьмом классе мурманского лицея № 1 по материалам данных учебника [1] и задачника [2] был проведён открытый урок «Многоэтажные дроби». Эта тема выбрана не случайно. В действующих учебниках она отражена мало (например, в учебнике под ред. С.А. Теляковского рассмотрен только один такой пример, решенный с помощью основного свойства дроби). Иногда «многоэтажность» заменяется традиционным действием деления, что приводит к громоздким и не всегда оправданным вычислениям. Однако на вступительных экзаменах в вузы часто встречаются задания, связанные с преобразованием многоэтажных дробей. На уроке мы попытались реализовать идею составления алгоритма преобразования многоэтажной дроби самими учащимися. На уроке каждому лицеисту был выдан комплект специальных материалов, в которых учащиеся работали карандашом. В случае если задание было выполнено неверно, ученик мог исправить свои записи с помощью ластика и тут же записать правильное решение. Это позволило учащимся чувствовать себя раскованно, не бояться делать ошибки, не ждать ответов других учеников.
В примерах теста (рис. 1-3), необходимо было найти выражения многоэтажными дробями. Выполнить задания теста, то есть для каждого выражения найти верный ответ, записанный в верхней строке, учащимся было предложено дома.
Алгоритм деления дроби на дробь был рассмотрен на предыдущих уроках (а также алгоритмы умножения и сложения дробей). Поэтому лицеисты уже знали, что стрелками обозначено действие умножение. Поставив стрелки в первой записи, они без труда, видя окончательный результат, расставили стрелки и во втором выражении.
Выполнив преобразование многоэтажной дроби по алгоритму, лицеисты убедились, что в подобных случаях сокращать нельзя. В примере 3 (рис. 2-3, внизу слева). необходимо было сначала сократить дробь, а затем применить алгоритм преобразования многоэтажной дроби. Учащиеся с большой заинтересованностью зачеркивали общие множители, рисовали стрелки и заполняли пропуски. Для того чтобы выяснить, как усвоен алгоритм преобразования многоэтажной дроби в конце урока была проведена игра. Каждый ученик получил листок с шуточными заданиями «Шторм на море» (рис. 4-1) и «Полицейские и воры» (рис. 4-2). Учащиеся самостоятельно преобразовывали «многоэтажную дробь»: сокращали (зачёркивали) общие множители, ставили стрелки и записывали получившийся результат в пустую рамочку. После выполнения всеми этого упражнения, сверили получившиеся результаты с ответами, оформленными на обороте классной доски. Одни учащиеся рисовали маяк, корабль, штурвал и якорь, другие записывали только начальные буквы этих слов (рис. 4-3). (На рисунках внизу: Ш – шериф, П – полицейский, М – мошенница, К – карманник). Все лицеисты без ошибок справились с этим необычным и интересным для них заданием. Работать с визуальными учебными материалами учащимся очень нравится, так как на этих уроках они творят сами, не созерцают со стороны работу учителя и более сильных учащихся, а принимают активное участие в решении той или иной учебной задачи и видят результаты своей работы тут же. Подобные уроки проходят у детей эмоционально, они чувствуют себя первооткрывателями, радуются своим успехам, стремятся выполнить как можно больше разнообразных заданий, попробовать свои силы при решении довольно сложных упражнений. Так как на таких уроках мало пишется, но много думается, то польза от них колоссальная. Распечатать комплект визуальных дидактических материалов по теме данной статьи.
Источник |