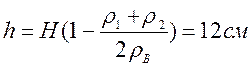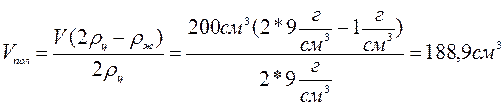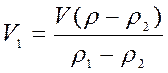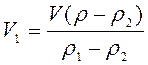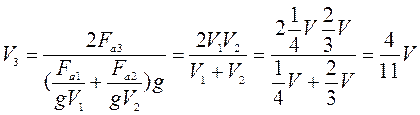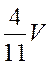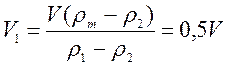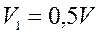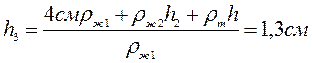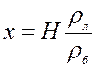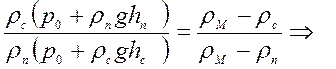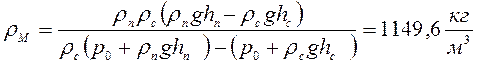- Цепочка муравьев длиной 1 м бежит с постоянной скоростью 15
- Олимпиада по физике для 7-11 классов
- Сегодняшняя задача про муравьев
- Сборник задач 7 класс
- Предисловие
- № 2.13 Велосипедист едет по дороге и через каждые 6 секунд проезжает мимо столба линии электропередачи. Увеличив скорость на некоторую величину ∆υ, велосипедист стал проезжать мимо столбов через каждые 4 секунды. Через какой промежуток времени он будет проезжать мимо столбов, если увеличит скорость еще на такую же величину?
Цепочка муравьев длиной 1 м бежит с постоянной скоростью 15
Траектория. Путь. Перемещение.
1.Автомобиль, двигаясь по кольцевой дороге радиус которой 10 км, сворачивает с кольцевой дороге и проезжает к центру, а затем поворачивает под прямым углом и выезжает на кольцевую дорогу. Найти путь и перемещение автомобиля.
2. Вертолет, пролетев 400 км, повернул на 60 градусов и пролетел еще 300 км. Найти путь и перемещение вертолета.
3.Изобразите траекторию движения, при котором путь превышает модуль перемещения в π/2 раза.
Прямолинейное равномерное движение
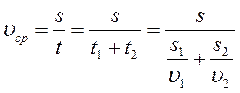
4. Мотоциклист проехал 5 км со скоростью 0,5 км/мин и следующие 4,6 км за 6 мин. Вычислите среднюю скорость движения за все время движения.
5.Два корабля движутся навстречу друг другу со скоростями 5 и 7 м/с. Второй корабль проходит мимо первого за 5 с. Найти длину второго корабля.
6.Движения двух велосипедистов заданы уравнениями х= 2t, х = 10-5t.
Найти время и место встречи.
Графическое представление движения
7. По приведенным на рисунке графикам опишите движения. Для каждого из них найдите начальную координату, модуль и направление скорости, запишите формулу х(t). Ответьте на вопросы:
1) Какие из тел встретятся, в каком месте, через какое время?
2) Каковы будут координаты тел через 4 с?
3) Через сколько времени координаты всех тел будут равны 20 м?
Относительность механического движения. Сложение перемещений и скоростей.
8. Воздушный шар подымается вертикально вверх со скоростью 3 м/с. Найти скорость шара, если подует западный ветер со скоростью 4 м/с.
9.Пешеход две трети своего времени движения шел со скоростью 3 км/ч. Оставшееся время — со скоростью 6 км/ч. Определите среднюю путевую скорость скорость движения пешехода.
10. Вдоль тропинки ползет цепочка муравьев со скоростью 2 см/с. Вожак во главе цепочки посылает «адъютанта» с поручением к замыкающему. Какова длина цепочки, если «адьъютант», передвигающийся со скоростью 3 см/с, вернулся к вожаку через 1 мин?
11. Если выпустить пулю, из пистолета (эксперимент на эту тему не проводить!!))) со скоростью 400 м/с, то она долетев до кучи песка проникает в нее на 36 см. Найти время движения пули внутри песка и ускорение.
12. Два железнодорожных состава прошли равный путь за одно и то же время, но, один состав, имея начальную скорость, равную нулю, прошел весь путь с ускорением 3 см/с2, а другой состав половину пути шел со скоростью 18 км/ч, а вторую половину пути со скоростью 54 км/ч. Найдите путь, пройденный составами.
Источник
Олимпиада по физике для 7-11 классов
Ищем педагогов в команду «Инфоурок»
Комплект заданий школьного тура олимпиады по физике включает в себя 4 задачи различного уровня сложности для 8-11 классов, для 7-го класса-3задачи.
Общая продолжительность для 11-9классов 1,5ч, для 7класса-1час.
Максимальное количество баллов: 40 баллов- 11-8классы, 30 баллов-7класс.
В муниципальный тур выходят ребята, набравшие не менее 50% от максимального балла.
Задания школьного этапа олимпиады школьников по физике
Автомобиль движется равноускоренно по прямой. При этом он проходит четыре последовательно расположенные метки A, B, C и D. Времена прохождения отрезков AB, BC и CD относятся, как 1:2:1 соответственно. Определите во сколько раз длина отрезка AD больше, чем длина отрезка BC.(10 баллов)
За какое время тело соскользнет с наклонной плоскости высотой h = 5,0 м, наклоненной под углом a = 45 0 к горизонту, если по плоскости с углом наклона b = 30 0 оно движется равномерно? (10 баллов)
Определить общее сопротивление проволочной сетки, изображенной на рисунке, если сопротивление каждого из звеньев R=8 Ом. Ответ выразить в Ом, округлив до целых. (10баллов)
В вертикально расположенном цилиндре под тяжёлым поршнем находится m=14 г азота. Какое количество теплоты получает газ при его нагревании от t 1 =25 0 C до t 2 =225 0 C? Ответ выразить в кДж, округлив до десятых. Молярная масса азота μ=28 г/моль, универсальная газовая постоянная R=8,31 Дж/(моль ⋅ К). (10 баллов)
Определить токи через все резисторы в цепи, схема которой изображена на рисунке. Напряжение, на источнике U. Сопротивления резисторов указаны на схеме. (15баллов)
Велосипедист двигался с постоянной скоростью. Заметив преграду, он начал тормозить с ускорением a=2 м/с 2 . После прохождения им S=36 м его скорость стала равной v =9 м/с. Чему была равна начальная скорость V 0 велосипедиста? Ответ выразить в м/с, округлив до целых.(5 баллов)
Определите силу трения в подвижном блоке, если при подъёме при помощи этого подвижного блока груза весом 200 Н на высоту 5м производят работу 1030Дж. (10баллов)
Против двух зеркал находится непрозрачный экран с вырезанным в нём отверстием в виде стрелки, на которое падает пучок параллельных лучей света. Постройте дальнейший ход лучей и определите положение изображения стрелки на экране. (10баллов)
Прямолинейный кусок проволоки массой 40г подвешен за середину. Левую половину куска согнули пополам, как показано на рисунке. Какой массы груз надо подвесить в точке перегиба, чтобы восстановить равновесие? Ответ приведите в граммах. (10баллов)
2. С какой высоты должна падать вода, чтобы при ударе о землю она закипала? На нагрев воды идёт 50% расходуемой механической энергии, начальная температура воды 20 0 С . (10баллов)
3. Кипятильник был подключен к батарее идеальных аккумуляторов с выходным напряжением U 0 =200В. Он смог прогреть стакан воды до температуры t 1 =85 ° C при температуре в комнате t комн =25 ° C. Потом второй такой же кипятильник подключили последовательно с этим и опустили во второй такой же стакан с водой. Какая температура t 2 установится в нем? Количество теплоты Δ Q , теряемое стаканом за время Δ t , пропорционально разности температур воды и воздуха, то есть Δ Q /Δ t = k ( t воды t возд ). Сопротивление кипятильника не зависит от его температуры. (10баллов)
4. Муравей бежит от муравейника по прямой так, что скорость его обратно пропорциональна расстоянию до центра муравейника. В тот момент, когда муравей находится в точке А на расстоянии l 1 =1м от центра муравейника, его скорость равна v 1 =2см/с . За какое время муравей добежит от точки А до точки В , которая находится на расстоянии l 2 =2м от центра муравейника? (10баллов)
Велосипедист проехал первую половину пути со скоростью V 1 = 10 км/ч. Затем он поехал с большей скоростью, но проколол шину. После попытки ликвидировать прокол велосипедист был вынужден оставшуюся часть пути пройти пешком. Чему равна средняя скорость движения велосипедиста на всем пути, если первую треть времени, затраченного им на вторую половину пути, он ехал со скоростью V 2 = 20 км/ч, вторую треть занимался проколом и последнюю треть шел пешком со скоростью V 4 = 5 км/ч? (10 баллов)
Определите плотность стекла, из которого сделан куб массой 857,5г, если площадь всей поверхности куба равна 294см 2 . (10 баллов)
Ученики 8 класса на уроках труда сделали модель воздушного шара. В каком случае подъемная сила у самодельного бумажного воздушного шара, заполненного горячим воздухом, больше: когда ребята запускают его в помещении школы или на дворе школы, где довольно прохладно? (10 баллов)
Однородный ровный стальной прут длиной 1 м согнули пополам под углом 90 о . На каком расстоянии от вершины прямого угла нужно подвесить прут, чтобы стороны получившегося угла оказались ориентированы по вертикали и горизонтали (см. рис.)? (10 баллов)
Таракан Митрофан совершает прогулку по кухне. Первые 10 секунд он шел со скоростью 0,1 м/с в направлении на север, повернул на запад и прошел 50 см за 10 секунд, затем 5 секунд постоял, а затем в направлении на северо– восток со скоростью 0, 2 м/с проделал путь 200 см, здесь его настигла нога человека.
Нарисуйте траекторию движения таракана и укажите его перемещение. Сколько времени гулял по кухне таракан Митрофан? Найдите среднюю скорость таракана Митрофана. (10баллов)
На рисунке в одном и том же масштабе изображены карандаш, плотно обвитый тонкой проволокой, и линейка. Определите цену деления линейки и диаметр проволоки. Результат измерения диаметра запишите с учетом погрешности. (10баллов)
Стеклянная пробка имеет внутри полость. Можно ли с помощью весов, набора гирь и мерного сосуда с водой определить объем полости, не разбивая пробки? Если можно, то как? Плотность стекла равна 2,5 г/см 3 .(10баллов)
Источник
Сегодняшняя задача про муравьев
Вот обычно, когда говорят «щенок пробежал начиная от последнего муравья в цепочке до первого», подразумевают, что муравьи и щенок двигались в одном направлении. А у тебя на рисунке цепочка муравьёв двигалась последним муравьём вперёд. Тут есть какая-то глубокая философия, мол, последние на самом деле первые. но обычно говорят, что такое решение неправильное: мол, ты молодец, но ты решал не ту задачу.
А вообще, конечно, можно только посочувствовать тем, кто не может просто написать вот так:
.
Слишком ты усложнил.
Туда — щенок пробежал всю длину цепочки муравьёв, плюс, расстояние, которое они прошли за это время (он же догонял первого).
Обратно — всю длину, минус то расстояние, которое они за это время прошли (последний двигался навстречу щенку).
В сумме — пробежал двойную длину цепочки.
В общем-то, это задача «на сообразительность». Если, конечно, чего не напутал.
Задача, кстати, для 7-го класса средней школы («Условия задач 1-го заочного тура 7-9 классы»)
Начали движение — какое расстояние щенок пробежал? Естественно, всю длину цепочки, плюс, расстояние, на которое она, (точнее, её начало — первый муравей) переместилась за это время. То есть, L+S. Правильно?
Теперь, щенок развернулся и побежал обратно. Какое расстояние он пробежал? В любом случае, он должен добежать до последнего муравья. Правильно? А какое это расстояние? Расстояние L (условие задачи). Но, последний же муравей, за это время прошёл (навстречу щенку) то же самое расстояние S. Правильно?
Теперь складываем: L+S+L+(-S)
2,41
скорость щенка в 2,41 раз выше скорости муравьев, следовательно,
S_щенка=96,4 м
Источник
Сборник задач 7 класс
Сборник задач по физике
Сборник задач повышенной сложности адресован учащимся 7-х классов, проявляющим интерес к изучению физики. Приводятся решения аналогичных задач и методические указания. Дается анализ ошибок, допускаемых учащимися при решении задач, связанных с недостаточно глубоким знанием предмета. На решенных примерах ученику будет легче самостоятельно анализировать ход решения задач. Последовательность расположения заданий соответствует содержанию учебного материала. В основе сборника — задачи, предлагавшиеся на олимпиадах по физике различного уровня.
Предисловие
Изучение школьного курса физики предполагает обучение одаренных школьников решению задач. При этом решение задачи рассматривается, как умение применять на практике, в каждом конкретном случае, общие положения физической науки. Именно поэтому умение решать задачи часто является определяющим критерием в оценке полноты и глубины усвоения теоретических знаний. Настоящее пособие написано с целью оказания помощи одаренным учащимся 7 — 8 классов и учителям школ при подготовке к олимпиадам по физике. Пособие представляет собой сборник задач по всем разделам школьного курса физики 7 класса, в который включены вопросы и задания различной степени сложности. Даются ответы и решения, раскрываются методы решения типовых задач.
Сборник задач можно использовать в факультативной и кружковой работе. Задачи, рассмотренные в пособии, взяты из сборников и составлены авторами.
Участие в олимпиадном движении играет большую роль в деле воспитания молодых людей. Ответственность за начатое дело, целеустремленность, трудолюбие, патриотизм. Учащиеся являются первыми помощниками учителя во всех делах. Это опора учителя, проводники его идей.
Олимпиадные задачи можно разделить на:
— поучительные и простые в решении с красивыми парадоксальными ответами. Они совершенствуют, а подчас вносят и серьёзные коррективы в мировоззрение ученика и, нередко, учителя. Иногда такая задача кажется внепрограммной, но решается и в пределах программы;
— элегантные, с казалось бы ограниченным набором данных или с избыточным числом переменных. Их назначение – шлифовка техники решения и анализа;
— внепрограммные – таких практически не бывает, встречаются только на международных олимпиадах. Связано это не только с желанием «срезать» участников, сколько с необходимостью уменьшить влияние разницы в программах различных стран и школ преподавания. С одной стороны, условия таких задач всегда сопровождаются подробным введением, с другой – содержат несколько вопросов разной степени сложности;
— громоздкие и достаточно сложные вычислительные задачи. Они малоинтересны после предварительного обсуждения, требуют много времени для решения, но важны для тренировки выносливости «олимпиадников», если таковые появились у преподавателя;
— действительно сложные, рассчитанные на самых продвинутых учеников и учителей. Допустимы на дополнительных занятиях в подготовленной аудитории, если не скучны;
Как правило, в решении олимпиадных задач можно выделить несколько привлекательных для анализа стадий:
— поначалу бывает непонятным условие (либо вообще неясно, о чём идёт речь, либо ситуация кажется настолько простой, что неясно, в чем же проблема);
— затем проводится анализ ситуации и после этого (или вместе с этим) построение модели явления – перевод каждой из словесных фраз в объяснении наблюдаемого явления на язык математики, запись уравнений, формул, условий;
— собственно решение и его анализ;
— выводы, обобщения и аналогии, снятие различного рода недоумении. Анализ необходимости сделанных при решении допущений. Чёткое фиксирование окончания решения.
ТЕМА I: СРЕДНЯЯ СКОРОСТЬ. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Автомобиль двигался первую половину пути со скоростью 60 км/ч, а вторую со скоростью 40 км/ч. Определить среднюю скорость движения автомобиля на всем пути.
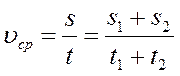
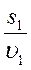
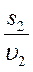
Ответ: 48
Мальчик два часа ехал на велосипеде, а потом шесть часов шел пешком. Какой была его средняя скорость, если ехал он втрое быстрее, чем шел, а шел со скоростью 4 км/ч?
Ответ: 6
Путешественник одну треть времени своего движения шел со скоростью 6 км/ч. Оставшееся время – со скоростью 3 км/ч. Определите среднюю скорость путешественника.
Ответ: 4
Мальчик проехал половину пути со скоростью 60 км/ч на автомобиле, оставшуюся часть пути он половину времени ехал со скоростью 45 км/ч, а последний участок – шел со скоростью 15 км/ч. Найти среднюю скорость перемещения мальчика на всем пути.
На участке дороги, где мальчик половину времени ехал со скоростью 45 км/ч, а вторую часть шел со скоростью 15 км/ч, среднюю скорость 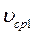
Средняя скорость мальчика на всем пути равна: 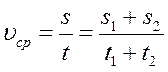
Ответ: 40
Мальчик половину времени всего движения ехал на велосипеде со скоростью 20 км/ч, половину оставшегося пути со скоростью 15 км/ч, а последний участок – шел со скоростью 6 км/ч. Какова средняя скорость на всем пути?
Найдем среднюю скорость на участках пути S 2 и S 3 (по условию задачи S 2 = S 3 ):
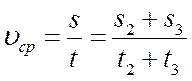
Тогда средняя скорость на всем участке пути:
Ответ: 14,3
Мальчик ехал сначала на автомобиле, а потом на велосипеде. Какую часть пути, и какую часть всего времени движения он ехал на автомобиле, если средняя скорость мальчика оказалась равной 24 км/ч, скорость езды на автомобиле
60 км/ч , а на велосипеде = 12 км/ч.
Запишем формулу для нахождения средней скорости:
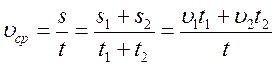
где t 1 = t — t 2 (2) подставим в (1) получим:
находим подобные:
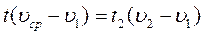
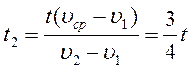
t 1 = t — 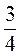
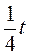
Теперь найдем путь, который проехал мальчик на автомобиле:
подставим (5) в (4):
получим:
Отсюда:
Ответ: t 1 = 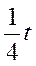
Средняя скорость автобуса на всем пути 60 км/ч, скорость между двумя пунктами 80 км/ч, причем остановки занимают 1 час. Найти расстояние между этими пунктами.
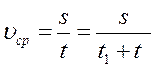
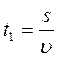
(2) подставляем в (1) 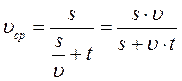
Из формулы (3) находим
Средняя скорость мотоциклиста на всем пути 20 км /ч. На второй половине пути мотоциклист двигался в 4 раза больше на чем на первой. Определите скорость мотоциклиста на обеих половинах пути.
Так как 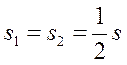
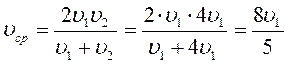
Из уравнения (1) найдем
Тогда
Ответ: 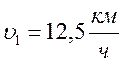
Мотоциклист проехал половину пути со скоростью 90 км/ч, оставшуюся часть пути он половину времени двигался со скоростью 60 км/ч, а последний участок пути со скоростью 30 км/ч. Найти среднюю скорость мотоциклиста на всем пути.
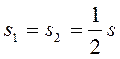
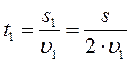
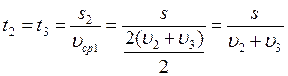
Найдем среднюю скорость мотоциклиста на всем пути:
Ответ:
Мальчик на мопеде первую половину пути двигался со скоростью в 1,5 раза большей, чем вторую половину пути. Средняя скорость мальчика на всем пути 15км/ч. Каковы скорости мальчика на первой и второй половинах пути?
Так как мальчик проехал одинаковые пути, то среднюю скорость можно найти по формуле:
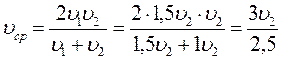
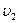
тогда
Ответ:
Первую половину пути мотоциклист двигался со скоростью 72 км/ч. Далее половину оставшегося времени он ехал со скоростью 60 км/ч, а затем шел пешком со скоростью 4 км/ч. Определить среднюю скорость движения на всем участке пути.
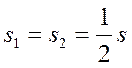
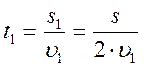
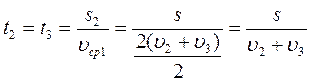
Найдем среднюю скорость мотоциклиста на всем пути:
Ответ:
Первую половину времени тело движется со скоростью 18 м/с под углом 30 0 к заданному направлению, а второй 120 0 к тому же направлению со скоростью 10м/с. Найти среднюю скорость перемещения.
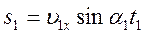
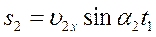
Ответ:
№ 1.13 Автомобиль проехал половину пути со скоростью υ1=60 км/ч, оставшуюся часть пути он половину времени шел со скоростью υ2 = 15 км/ч, а последний участок со скоростью υ3 = 45 км/ч. Найти среднюю скорость автомобиля на всем пути.
Определим среднюю скорость:
Найдем время на каждом участке пути:
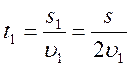
υср =
№ 1.14 Поезд первую половину пути шел со скоростью в n = 1,5 раза большей, чем вторую половину. Средняя скорость поезда на всем пути υср=43,2км/ч.
Каковы скорости поезда на первой (υ1) и второй (υ2) половинах пути.
Найдем время на каждом участке пути:
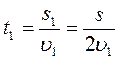
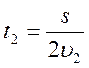
Определим среднюю скорость: υср = 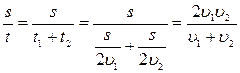
υср = 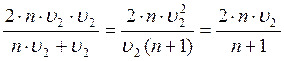
Из (3) уравнения выразим 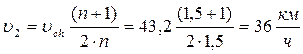
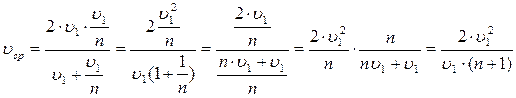
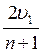
Из (5) уравнения находим 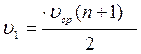
Ответ: 36 км/ч , 54 км/ч.
1.15 Когда спортсмен-любитель, совершая пробежку вдоль трамвайной линии, поравнялся с остановкой, от нее одновременно отошли два трамвая (в противоположных направлениях). Через 4 мин. 10 с после этого он встретил идущий ему навстречу трамвай, а еще через 2 мин. 5 с его обогнал трамвай. Определите скорость и интервал движения трамваев, если скорость спортсмена 8 км/ч. Время, которое трамвай стоит на остановке, очень мало.
Пусть остановка находится в точке O (рис.), первый трамвай встретился спортсмену точке A через время t 1 , а второй – в точке B через время t 2 .
Тогда для этих времен можно записать:
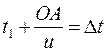
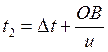
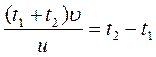


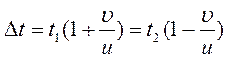

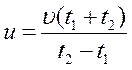
Теперь можно найти и интервал движения
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Автомобиль двигался первую половину пути со скоростью 70 км/ч, а вторую со скоростью 50 км/ч. Определить среднюю скорость движения автомобиля на всем пути.
Велосипедист двигался первую половину пути со скоростью 20 км/ч, а вторую со скоростью 15 км/ч. Определить среднюю скорость движения велосипедиста на всем пути.
Пешеход шел первую половину пути со скоростью 15 км/ч, а вторую со скоростью 10 км/ч. Определить среднюю скорость движения пешехода на всем пути. (Ответ: 12 км/ч)
Мальчик двигался первую половину пути на велосипеде со скоростью 18 км/ч, а вторую шел пешком со скоростью 6 км/ч. Определить среднюю скорость движения мальчика на всем пути. (Ответ: 9 км/ч)
Мальчик три часа ехал на велосипеде, а потом пять часов шел пешком. Какой была его средняя скорость, если ехал он вдвое быстрее, чем шел, а шел со скоростью 3 км/ч?
Пешеход две трети времени своего движения шел со скоростью 5 км/ч. Оставшееся время – со скоростью 2 км/ч. Определите среднюю скорость путешественника.
Путешественник четыре пятых времени своего движения шел со скоростью 5 км/ч. Оставшееся время – со скоростью 2 км/ч. Определите среднюю скорость путешественника. (Ответ: 4,4 км/ч)
Велосипедист одну треть времени своего движения ехал со скоростью 4 км/ч. Оставшееся время – со скоростью 7 км/ч. Определите среднюю скорость путешественника.
Турист проехал половину пути со скоростью 50 км/ч на автомобиле, оставшуюся часть пути он половину времени ехал со скоростью 35 км/ч, а последний участок – шел со скоростью 10 км/ч. Найти среднюю скорость перемещения туриста на всем пути. (Ответ: 31 км/ч)
Мальчик половину времени всего движения ехал на велосипеде со скоростью 25 км/ч, половину оставшегося пути со скоростью 12 км/ч, а последний участок – шел со скоростью 5 км/ч. Какова средняя скорость на всем пути? (Ответ: 16 км/ч)
Средняя скорость поезда на всем пути 90 км/ч, скорость между двумя пунктами 70 км/ч, причем остановки занимают 2 часа. Найти расстояние между этими пунктами.
Средняя скорость пешехода на всем пути 10 км /ч. На второй половине пути пешеход шел в 1,3 раза быстрее, на чем на первой. Определите скорость пешехода на обеих половинах пути. ( Ответ: 8,85 км/ч; 11,5 км/ч)
Средняя скорость автомобилиста на всем пути 72 км /ч. На первой половине пути автомобилист ехал в 3 раза быстрее, на чем на второй. Определите скорость автомобилиста на обеих половинах пути. ( Ответ: 48 км/ч; 144 км/ч)
На первой половине пути путешественник шел в 1,5 раза быстрее, на чем на второй. Средняя скорость путешественника на всем пути 8 км/ч. Определите скорость путешественника на обеих половинах пути.
( Ответ: 6,67 км/ч; 10 км/ч)
Мотоциклист проехал половину пути со скоростью 100 км/ч, оставшуюся часть пути он половину времени двигался со скоростью 70 км/ч, а последний участок пути со скоростью 40 км/ч. Найти среднюю скорость мотоциклиста на всем пути. ( Ответ: 71 км/ч)
Путешественник первую половину пути шел со скоростью в 2 раза большей, чем вторую половину пути. Средняя скорость путешественника на всем пути 8 км/ч. Каковы скорости путешественника на первой и второй половинах пути?
( Ответ: 6 км/ч; 12 км/ч)
Велосипедист первую половину пути ехал со скоростью в 1,6 раза большей, чем вторую половину пути. Средняя скорость велосипедиста на всем пути 12 км/ч. Каковы скорости велосипедиста на первой и второй половинах пути?
( Ответ: 9,75 км/ч; 15,6 км/ч)
Первую половину пути мальчик двигался со скоростью 4 км/ч. Далее половину оставшегося времени он ехал на велосипеде со скоростью 36 км/ч, а затем шел пешком со скоростью 3 км/ч. Определить среднюю скорость движения на всем участке пути. ( Ответ: 6,64 км/ч)
Пешеход две трети своего движения шел со скоростью 3 км/ч. Оставшееся время – со скоростью 6 км/ч. Определите среднюю скорость пешехода. (Ответ: 4 км/ч)
Автомобиль первую четверть пути проехал с постоянной скоростью за половину всего времени движения. Следующую треть пути, также двигаясь с постоянной скоростью, – за четверть всего времени. Остаток пути был преодолен со скоростью v 3 = 100 км/час. Какова средняя скорость автомобиля на всем пути? Чему равны скорости на первом и втором участках? (Ответ: средняя скорость 60 км/ч, скорость на первом участке 30 км/ч, а на втором 80 км/ч.)
ТЕМА 2: ОТНОСИТЕЛЬНОСТЬ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Из Астаны в Караганду с интервалом в 10 минут вышли два электропоезда со скоростями 30 км/ч. С какой скоростью двигался поезд, идущий в Астану, если он повстречал эти электропоезда через 4 минуты один после другого?
Найдем путь, который прошел 1-й электропоезд за 10 минут:
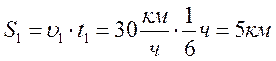
Скорость приближения встречных электропоездов:
Тогда скорость скорость движения поезда идущего из Астаны найдем:
Ответ:
Катер идет по течению реки из пункта А в пункт В и обратно. Время движения туда – 3 часа, а обратно – 6 часов. Сколько времени потребуется для того, чтобы пройти расстояние между пунктами А и В по течению при выключенном моторе?
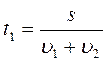
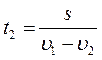
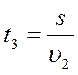
Подставим (3) в (1) и (2):
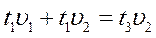
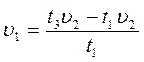
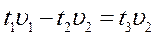
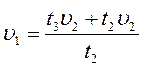
Приравняем (4) и (5) 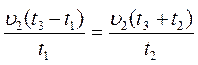
Ответ:
Мимо пристани по реке Иртыш проплывает плот. В этот момент в Павлодар, находящийся на расстоянии 15 км от пристани, вниз по реке отправляется катер. Он доплыл до Павлодара за время 45 минут и, повернув обратно, встретил плот на расстоянии 9 км от поселка. Каковы скорость течения реки и скорость катера относительно воды?
Систему отсчета свяжем с плотом (П). В этой системе отсчета катер движется вниз и вверх по реке с одинаковой скоростью. Это значит, что время удаления катера от плота равно времени приближения к нему; таким образом, катер также возвращался 45 минут.
Тогда за 1,5 часа плот прошел расстояние S = S 1 — S 2 = 6 км.
Следовательно, скорость плота относительно берега:
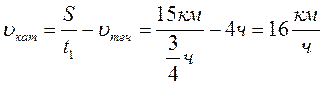
Ответ: 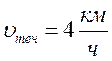
Теплоход проходит расстояние между двумя пунктами на реке вниз по течению за 50 часов, а обратно – за 70 часов. Сколько суток между этими пунктами плывут плоты?
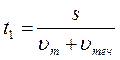
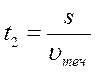
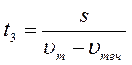
Преобразуем (1) и (3) формулы:
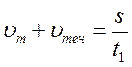
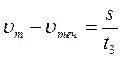
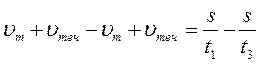
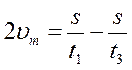
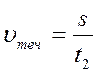
(2) подставим в (4) 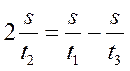
отсюда следует: 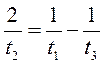
Ответ:
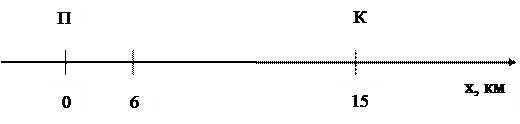
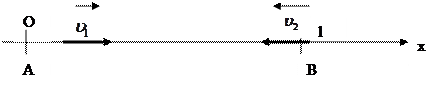
№ 2.5 Группа туристов, двигаясь цепочкой по обочине дороги со скоростью 3,6 км/ч, растянулась на 200 м. Замыкающий посылает велосипедиста к вожатому, который находится впереди группы. Велосипедист едет со скоростью 7 м /с; выполнив поручение, он тут же возвращается к замыкающему группы с той же скоростью. Через сколько времени после получения поручения велосипедист вернулся обратно?
Свяжем СО с группой туристов. Скорость велосипедиста в системе отсчета, связанной с колонной, равна 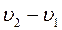
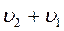
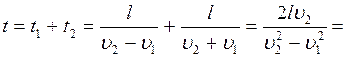
№ 2.6 Путешественник, глядя в окно вагона, заметил, что два встречных поезда прошли мимо него через 7 минут один после другого. Через какой промежуток времени один после другого отправились эти поезда со станции, если все три поезда движутся с одинаковыми скоростями?
Примем за точку отсчета поезд путешественника. Тогда скорость сближения 2 – го поезда с путешественником равна: υ = 2υ1. Путь, который пройдет 2-й поезд до встречи с путешественником равен s =2υ1· 7 мин = 14 υ1 (м). Тогда время, через которое отправятся поезда со станции один после другого равно:
t = 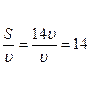
Ответ: через 14 мин.
№ 2.7 Из пунктов А и В, расстояние между которыми равно l, одновременно навстречу друг другу начали двигаться два тела: первое со скоростью 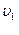
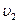
За точку отсчета выберем пункт А:
Запишем для первого и второго тела уравнение движения:
х1= 0 + 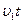
Во время встречи х1 = х2, тогда приравнивая правые части уравнений (1) и (2) получим: 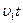
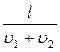
Подставим(3) уравнение в (1) получим расстояние от точки А до места их встречи:
хс = 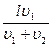
Ответ: t = 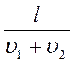
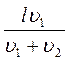
№ 2.8 Моторная лодка проходит расстояние между двумя пунктами А и В по течению реки за время t 1 = 3ч, а плот за время t = 12 ч. Сколько времени t 2 затратит моторная лодка на обратный путь?
За точку отсчета выберем пункт А:
Обозначим υ — скорость лодки относительно воды, а u — скорость плота, можно записать:
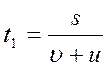
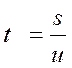
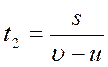
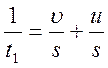
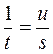
Вычтем из уравнения (4) удвоенное уравнения (5), получаем:
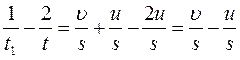
Также перепишем уравнение (3): 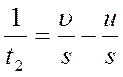
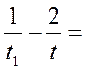
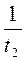
t 2 =
Подставляем числовые значения:
№ 2.9 Между двумя пунктами, расположенными на реке на расстоянии 
За точку отсчета выберем пункт А:
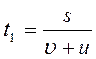
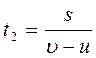
Решая совместно два уравнения, находим:
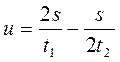
из (1) уравнения находим 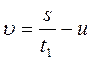
Ответ: 
№ 2.10 На соревнованиях по плаванию два пловца стартуют одновременно. Первый проплывает длину бассейна за 1,5 минуты, а второй — за 70 секунд. Достигнув противоположного края бассейна, каждый пловец разворачивается и плывет в другую сторону. Через какое время после старта второй пловец поравняется с первым, обойдя его на один «круг»?
Чтобы обойти первого пловца на один «круг», второму нужно «догнать» первого. Скорость их сближения υ= υ2 – υ1.
Можно считать что изначально первый пловец впереди второго на 2L.
№ 2.11 На большой плоской поляне в лесу на расстоянии 20 м друг от друга находятся два муравейника. Ровно в полдень из муравейников выбегают и сразу разбегаются равномерно во все стороны с одинаковыми скоростями многочисленные и злобные муравьи воины. Встретившись с врагом из другого муравейника, воин вступает в бой. Силы практически равны. Так что в кратковременном бою погибают два бойца. Через какое время погибнет ровно четверть выбежавших насекомых? Скорость муравья 0,02 м/с, все муравьи выбегают из муравейника одновременно.
Раньше всех встретятся друг с другом муравьи
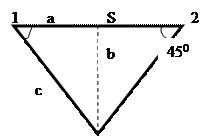
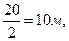
с=
На это потребуется время
№ 2.12 Эскалатор метро опускает идущего по нему человека за 1 мин. Если человек будет идти вдвое быстрее, то он спустится за 45 с. Сколько времени спускается человек, стоящий на эскалаторе.
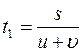
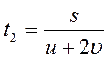
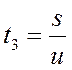
из (1) и (2) следует s = t 1 (υ +u ) s = t 2 (2υ +u )
( t 1 — t 2 ) u = (2 t 2 — t 1 ) υ , (4) подставляя в выражение (4) цифровые данные и найдём соотношение между υ и u: u=2υ (5)
из (1) следует s = 3υt1, (6) тогда
№ 2.13 Велосипедист едет по дороге и через каждые 6 секунд проезжает мимо столба линии электропередачи. Увеличив скорость на некоторую величину ∆υ, велосипедист стал проезжать мимо столбов через каждые 4 секунды. Через какой промежуток времени он будет проезжать мимо столбов, если увеличит скорость еще на такую же величину?
Ответ: через 3 с.
№ 2.14 Человек бежит по эскалатору. В первый раз он насчитал n1 = 50 ступенек, во второй раз, двигаясь в ту же сторону со скоростью втрое большей, он насчитал n2 = 75 ступенек. Сколько ступенек он насчитал бы на неподвижном эскалаторе?
Если бы скорость человека была направлена противоположно направлению движения эскалатора, то он насчитал бы тем меньше ступенек, чем быстрее шел (но не меньше n). В нашем же случае направления скоростей человека и эскалатора совпадают.
Пусть υ – скорость движения эскалатора; l – его длина и n – число ступенек на неподвижном эскалаторе. Число ступенек, приходящихся на единицу длины эскалатора, равно n/l. Поэтому, если человек идет со скоростью u ,
то время его пребывания на эскалаторе: 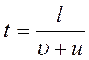
а путь, пройденный по эскалатору: 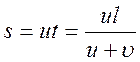
При этом человек насчитывает число ступенек:


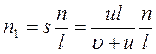
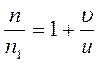
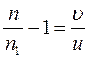

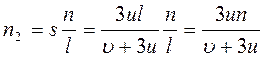
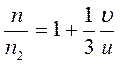
уравнение (3) подставляем в (4) исключая отношение 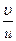


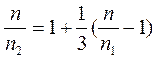
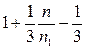
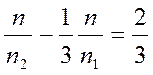
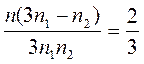
Ответ: 100 ступенек.
Два тела движутся навстречу друг другу так, что за каждые 15 секунд расстояние между ними уменьшается на 30 м. Если эти тела будут двигаться в одном направлении с прежними по величине скоростями, то за 10 с расстояние между ними увеличится на 4 м. С какой скоростью движется каждое из этих тел?
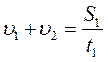
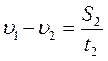
из (2) уравнения находим: 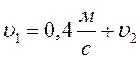
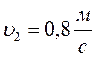
Ответ: 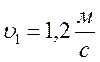
Когда хвост ползущего Удава поравнялся с пальмой, под которой сидела Мартышка, она, решив измерить длину Удава, побежала вдоль него и положила банан рядом с его головой. Затем Мартышка побежала обратно и положила второй банан рядом с кончиком хвоста Удава. Потом пришел Попугай и измерил расстояния от пальмы до каждого из бананов, которые оказались равными 16 и 48 попугаев. Найдите длину Удава в попугаях, а также определите, во сколько раз быстрее бегает Мартышка, чем ползает Удав.
Пусть L – длина Удава, υ – скорость бегущей Мартышки, u – скорость ползущего Удава, t 1 – время забега Мартышки до головы Удава, t 2 – время забега в обратном направлении.
Тогда в системе отсчета, связанной с ползущим Удавом, для прямого и обратного забега Мартышки можно составить следующие два уравнения:
(υ- u) = 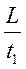
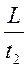
Аналогичные уравнения, записанные в системе отсчета, связанной с пальмой, будут иметь вид:
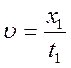
Здесь x 1 =48 и x 2 =16 – координаты первого и второго бананов, выраженные в Попугаях. Решая эту систему четырех уравнений, получим, что L=38,4 попугая, 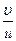
Ответ: 38,4 попугая. В 5 раз.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Катер идет по течению реки из пункта А в пункт В и обратно. Время движения туда – 4 часа, а обратно – 8 часов. Сколько времени потребуется для того, чтобы пройти расстояние между пунктами А и В по течению при выключенном моторе?
Расстояние между двумя пристанями моторная лодка проходит по течению за 15 мин, а против течения – за 45 мин. За какое время это расстояние проплывет по течению спасательный круг, упавший в воду? (Ответ: 45 минут)

(Ответ: 120 минут)
Из Астаны в Костанай с интервалом в 20 минут вышли два поезда со скоростями 60 км/ч. С какой скоростью двигался поезд, идущий в Астану, если он повстречал эти электропоезда через 8 минут один после другого?
Два тела движутся навстречу друг другу так, что за каждые 10 секунд расстояние между ними уменьшается на 16 м. Если эти тела будут двигаться в одном направлении с прежними по величине скоростями, то за 5 с расстояние между ними увеличится на 3 м. С какой скоростью движется каждое из этих тел? ( Ответ: 1,1м/с; 0,5 м/с)
Скорость катера относительно воды 7 м/с, скорость течения реки 3 м/с. Когда катер двигался против течения, с него сбросили в воду поплавок. Затем катер прошел против течения 4,2 км, повернул обратно и догнал поплавок. Сколько времени двигался катер? ( Ответ: 35 минут)
Эскалатор метро опускает идущего по нему человека за 2 мин. Если человек будет идти втрое быстрее, то он спустится за 90 с. Сколько времени спускается человек, стоящий на эскалаторе. (Ответ: 6 мин)
Человек, идущий вниз по опускающемуся эскалатору, затрачивает на спуск 1,5 минуты. Если человек будет идти вдвое быстрее, он затратит на 30 секунд меньше. Сколько времени он будет спускаться, стоя на эскалаторе?
Самолет летит из пункта А в пункт В и возвращается обратно. Скорость самолета в безветренную погоду равна 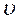
( Ответ: 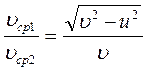
Теплоход проходит расстояние между двумя пунктами на реке вниз по течению за 60 часов, а обратно – за 80 часов. Сколько суток между этими пунктами плывут плоты?
Моторная лодка проходит расстояние между двумя пунктами А и В по течению реки за 3 часа, а плот за 12 часов. Сколько времени моторная лодка затратит на обратный путь?
Моторная лодка проходит по реке от пункта А до пункта В расстояние за 4 часа, а обратно за 5 часов. Определите скорость течения реки, если расстояние между пунктами 80 км. Скорость лодки относительно воды оставалась все время одной и той же. (Ответ: 2 км/ч)
Из двух пунктов, расстояние между которыми 100 м, одновременно навстречу друг другу начали двигаться два тела. Скорость одного из них 20 м/с. Какова скорость второго тела, если они встретились через 4 с? (Ответ: 5 м/с)
Путешественник шел вдоль железнодорожного полотна со скоростью 4 км/ч. Он заметил, что по путям идут две встречные электрички, одна из которых составлена из 9 вагонов, а другая из 10 вагонов. Путешественник обратил внимание на то, что головные вагоны поравнялись друг с другом как раз напротив него. Путешественник удивился, когда увидел, что и последние вагоны разошлись тоже строго напротив него. Путешественнику стало любопытно, с какой скоростью идут электрички. Если считать их скорости равными. ( Ответ: 76 км/ч)
На соревнованиях по плаванию два пловца стартуют одновременно. Один из них проплывает длину бассейна за 1,5минуты, а другой – за 70 секунд. Достигнув противоположного края бассейна, каждый пловец разворачивается и плывет в другую сторону. Через какое время после старта пловцы встретятся? (Ответ: 78,75с)
Знайка живет в доме, стоящем около дороги между остановками A и B на расстоянии 800 м от A. В направлении от A к B по дороге каждый день проезжают автобус со скоростью 40 км/ч и трамвай со скоростью 20 км/ч. На остановку B они приезжают одновременно в 8 часов утра. В какое самое позднее время должен выйти из дома Знайка, чтобы успеть уехать на автобусе? на трамвае? Знайка ходит со скоростью 4,8 км/ч, расстояние между остановками 2 км. Время, которое транспорт стоит на остановке, очень мало. (Ответ: чтобы успеть на автобус, Знайка должен выйти в 7.47, а чтобы успеть на трамвай – в 7.45).
Крокодил Гена ездит на работу в зоопарк на автобусе, который всегда ходит точно по расписанию. Домик Гены стоит около дороги между остановками A и B на расстоянии l от остановки A. Автобус едет в направлении от A к B с постоянной скоростью V. Найдите, за какой минимальный промежуток времени до прибытия автобуса на остановку B Гена должен выходить из дома, чтобы успеть на него, если крокодил ходит со скоростью U, а время, в течение которого автобус стоит на остановке, пренебрежимо мало. Расстояние между остановками равно L. (Ответ: за
при 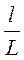
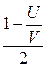
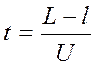
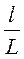
ТЕМА 3: МАССА. ПЛОТНОСТЬ. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
№ 3.1 Масса сплошного куба, сделанного из некоторого вещества, равна 2,5 кг. Какую массу будет иметь куб, если длину его ребра уменьшить в два раза?
Объем куба с ребром, уменьшенным в два раза: V 1 = 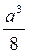
а масса куба с ребром, уменьшенным в два раза: m 1 = ρ 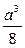
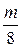
m 1 =
№ 3.2 Кусок сплава из свинца и олова массой 664 г имеет плотность 8,3г/см 3 . Определите массу свинца в сплаве. Принять объем сплава равным сумме объемов его составных частей.
Пусть V 1 , m 1, ρ 1 – объем, масса, плотность свинца.
V 2 , m 2, ρ 2 – объем, масса, плотность олова
Найдем объем сплава: 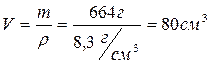
Масса сплава равна: m = m 1 + m 2 , m 2 = m — m 1 (1)
Плотность свинца и олова соответственно равны: 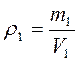
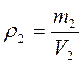
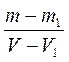
Решая уравнение (3) выразим 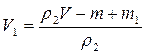
Подставим уравнение (4) в (2): 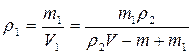
Найдем из уравнения (5) 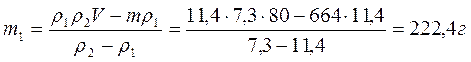
Ответ: 222,4 г свинца
№ 3.3 Сплав золота и серебра массой 400 г имеет плотность 14000 кг/м 3 . Полагая объем сплава равным сумме объемов его составных частей, определить массу золота и его процентное содержание в сплаве.
Найдем объем сплава: 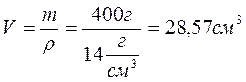
Масса сплава равна: m = m 1 + m 2 , m 2 = m — m 1 (1)
Плотность золота и серебра соответственно равны: 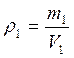
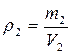
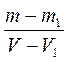
Решая уравнение (3) выразим 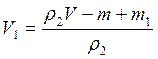
Подставим уравнение (4) в (2): 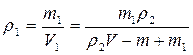
Найдем из уравнения (5) 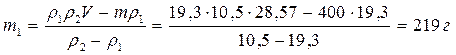
Ответ: 219 г (золота); 54,75%
№ 3.4 В куске кварца содержится небольшой самородок золота. Масса куска 100 г, а его плотность 8 г /см 3 . Определите массу золота, содержащегося в кварце. Принять, что плотности кварца и золота соответственно равны 2,5 и 19,36г/см 3 .
Найдем объем куска 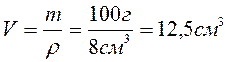
Объем куска равен: V = V 1 + V 2 = 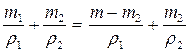
Ответ: 77,48 г золота.
Исследование историков показали, что Буратино был изготовлен не из одного полена, а из двух поленьев. Его голову папа Карло выточил из дуба, а остальные части тела выстрогал из сосны, известно, что плотность дуба 690 кг/м 3 . вес изготовленной из него части тела составляет треть от веса Буратино, а объем только четверть. Найдите плотность соснового полена.
m, V , 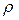
Тогда 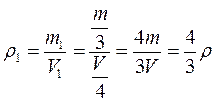
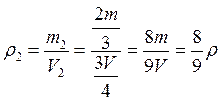
Из (1) и (2) находим
Ответ:
Стакан, заполненный до краев водой, имеет массу 214,6 кг. Когда в этот стакан с водой поместили небольшой камень массой 29,8 г и часть воды вылилась наружу, масса стакана с содержимым оказалась равной 232 г. Определить плотность вещества камня.
Пусть m1 – масса воды в стакане
m3 – масса стакана с содержимым
∆m1=m2— m3 = 202,2 г (масса воды, которая осталась в стакане)
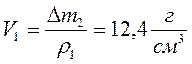
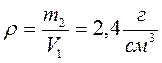
Ответ:
Железная и алюминевая детали имеют одинаковые объемы. Найдите массы этих деталей, если масса железной детали на 12,75 г больше больше массы алюминевой.
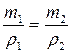
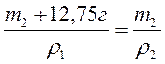
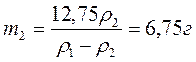
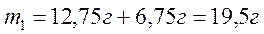
Ответ:
Сплав состоит из олова массой 2,92 кг и свинца массой 1,13 кг. Какова плотность сплава, если считать, что объем сплава равен сумме объемов его составных частей.
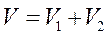
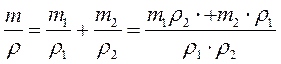
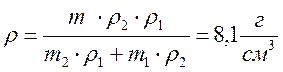
Ответ:
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Какова плотность железного дерева, если она в 34 раза больше, чем у эсхиномена щетинистоволосистого (самое легкое дерево), и если изделие из него при массе 700 г имеет объем 16 дм 3 ? (Ответ: 1490 кг/м 3 )
Самый большой сыр, изготовленный в США в 1988 г., имел массу 18 171 кг. Какова плотность сыра, если для его перевозки потребовался бы кубический контейнер с длиной ребра 2,54 м? (Ответ: 1100 кг/м 3 )
Самый большой медальон из золота в виде монеты, изготовленный в Канаде в 1986 г., имеет диаметр 95,25 см и толщину 19,05 мм. Плотность золота 19300 кг/м 3 . Какова его масса? (Ответ: 263 кг)
Самый большой шлюз в Бельгии имеет размеры 500м х 57м х 23 м. Сколько морской воды плотностью 1030 кг/м 3 он вмещает? (Ответ: 675 165 т.)
Кусок сплава из свинца и олова массой 550 г имеет плотность 8,2 г/см 3 . определить массу свинца в сплаве. Принять объем сплава равным сумме объемов его составных частей.
(ρ1 =11300 кг/м 3 –свинец; ρ2 =7300 кг/м 3 — олово).
( Ответ: m 1 = 172 г, m 2 = 378 г)
Пробирка, наполненная водой, имеет массу 44 г. Эта же пробирка, но с кусочком стали массой 10 г, доверху залитая водой, имеет массу 52,7 г. Определить плотность стали, помещенной в пробирку. (Ответ: 7,7 г/см 3 ).
Золотая и серебрянная детали имеют одинаковые объемы. Найдите массы этих деталей, если масса золотой детали на 15г больше больше массы сребрянной. Плотность золота – 19,3 г/см 3 , серебро – 10,5 г/см 3 . ( Ответ: 32,9 г ; 17,9 г)
Сплав состоит из меди массой 3 кг и алюминия массой 1,3 кг. Какова плотность сплава, если считать, что объем сплава равен сумме объемов его составных частей. Плотность меди-8,9 г/см 3 ; алюминия — 2,7 г/см 3 . (Ответ: 5,25 г/см 3 )
Сплав состоит из олова массой 2,92 кг и свинца массой 1,13кг. Какова плотность сплава, если считать, что объем сплава равен сумме объемов его составных частей?
(Ответ: 8100 кг/м 3 ).
Прибор для измерения плотности жидкости – ареометр – в простейшем случае представляет собой цилиндрическое тело, внутри нижней части которого закреплен груз, обеспечивающий устойчивое плавание ареометра в вертикальном положении, а на боковую поверхность нанесена шкала плотностей так, что при плавании ареометра в однородной жидкости он погружается точно до отметки, соответствующей ее плотности. В широкий и глубокий сосуд с водой поверх нее налит слой бензина толщиной h=10 см. Какую плотность покажет ареометр массой M=10 грамм, опущенный в этот сосуд? Как изменятся его показания, если толщину слоя бензина увеличить вдвое? Считайте, что диаметр ареометра намного меньше диаметра сосуда. Плотность воды 1,0 г/см 3 , бензина 0,75 г/см 3 , площадь поперечного сечения ареометра 1 см 2 .
(Ответ: 0,8 г/см 3 ; 0,75 г/см 3 )
ТЕМА 4: СИЛЫ В МЕХАНИКЕ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. СИЛЫ В ПРИРОДЕ

К трем динамометрам, соединенным так, как показано на рисунке, подвешен груз. Показания верхнего и нижнего динамометров 90 Н и 30 Н соответственно. Определите показания среднего динамометра.

Пусть m — масса динамометра, M — масса груза, а T1, T2, T3 — показания динамометров. Каждый динамометр показывает вес груза, привешенного к нему снизу + его собственный вес, т.к. вес корпуса динамометра при таком способе подвешивания растягивает пружину динамометра.
T1 = 90 Н = 3mg + Mg (1)
T2 = 2mg + Mg (2)
T3 = 30 Н = mg + Mg (3)
Из первого и третьего уравнения находим:
Mg =90 — 3 mg 90 – 3 mg = 30 – mg; mg = 30 Н (4)
Четвертое уравнение подставляем в первое: 90 =3*30 + Mg => M = 0 кг,
Из второго уравнения находим T 2 = 2*30 + 0 =60 Н
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
4.1. На горизонтальной поверхности стола лежит однородная цепочка. Когда часть цепочки длиной 15 см свешивается со стола, цепочка начинает скользить. Коэффициент трения цепочки о поверхность стола 0,02. Какова длина цепочки? (Ответ 0,9 м)
4.2. Чтобы удержать брусок массой 2 кг на наклонной плоскости с углом наклона 30o, к нему приложили силу, направленную вдоль наклонной плоскости. Коэффициент трения между бруском и поверхностью плоскости 0,2. Чему равна эта сила? (Ответ 6,54 Н)
4.3. Тележка длиной 2 м с покоящимся на ее краю грузом движется со скоростью 3 м/с и резко останавливается. Определить минимальный коэффициент трения между грузом и поверхностью тележки, если в момент соскальзывания груза с противоположного края тележки его скорость оказалась в три раза меньше первоначальной.
ТЕМА 5: РАБОТА. ЭНЕРГИЯ. ПРОСТЫЕ МЕХАНИЗМЫ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Из воды с глубины 5 м поднимают до поверхности камень объемом 0,6 м 3 . Плотность камня 2500 кг/м 3 . Найти работу по подъему камня.
При всплывании бревна с глубины 5 м сила Архимеда совершила работу 4 кДж. Какова масса бревна? Плотность древесины 700 кг/м 3 .
A = m 1 · g · h m 1 =
запишем уравнение: mg = Fa ;
ρт· V·g = ρж · 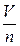
m =
Площадь поршней гидравлического пресса 2 см 2 и 400 см 2 . O пределите силу давления на больший поршень и высоту его поднятия, если при опускании малого поршня на 20 см производится работа 10 Дж.
A = F 1 · S 1 , F 1 = 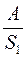
F 1 · S 2 = F 2 · S 1 F 2 = 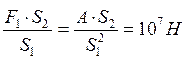
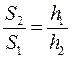
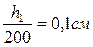
Ответ: F 2 = 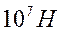
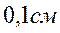
Высота плотины гидроэлектростанции 12 м, мощность водяного потока 3 МВт. Найдите объем воды, падающей с плотины за 1 минуту.
выражаем и вычисляем объем воды:
Ответ:
Сила тяги тепловоза равна 245 кН. Мощность двигателей 3000 кВт. За какое время поезд при равномерном движении пройдет путь, равный 15 км?
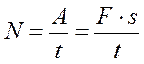
Какую мощность необходимо развить, чтобы сжать пружину на 4 см в течение 5с, если для сжатия её на 1 см требуется сила 24,5 кН?
При сжатии пружины возникает сила упругости: 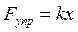
Ответ:

Левое плечо легкого рычага имеет длину

ρВ = 1 г/см 3 , g = 10 Н/ кг.

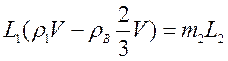

L 2 (m2g — ρвg 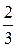
L2(ρстV — ρв 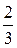
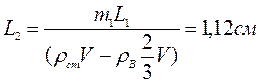
Ответ: 1,12 см.

На рисунке представлена система из трех блоков и грузов. Крайние грузы сделаны из алюминия и имеют плотность ρ1 = 2700 кг/м 3 . Масса левого груза m = 2 кг. Средний груз представляет собой кусок пластилина с плотностью ρ2 = 1100 кг/м 3 . Система находится в равновесии. Какой объем пластилина следует прилепить к среднему грузу, чтобы система находилась в равновесии, когда все грузы опущены в воду? Плотность воды ρ0 = 1000 кг/м 3 .
ρ0 = 1000 кг/м 3 — плотность воды, V — начальный объем пластилина, V’ — требуемый объем пластилина в воде.
Трение отсутствует, натяжение нити постоянно вдоль её длины, грузы неподвижны, поэтому масса правого крайнего груза так же равна m. Так как плотности крайних грузов равны, то равны и их объемы.
Вес среднего груза равен двум силам натяжения нити, следовательно, его масса равна 2m.
Пусть теперь равновесие установлено в воде. Результирующая сил Архимеда и тяжести, действующих на каждый из крайних грузов, mg=ρ s gV; mg = ρ s g 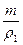
которая уравновешивается силой натяжения нити, равна
( m — ρж 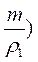
Аналогичная результирующая для куска пластилина равна (ρ2-ρ0)V’g
Сила натяжения нити, на которой висит пластилин, вдвое больше силы натяжения нити, на которой висят крайние грузы. Поэтому
ΔV = V’ — V = V’ — 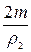
Ответ: нужно прилепить ≈ 21,6 дм 3 пластилина.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Почему, спускаясь по канату «на руках», можно обжечься? Какое количество теплоты может выделиться, если высота каната h = 5 м, а масса человека m = 70 кг?
№ 5.2 Перекидывая легкую нить с привязанными к ее концам грузами через блок, ученик заметил, что она находится в равновесии, если массы грузов различаются не более чем в 2 раза, и соскальзывает в противном случае. Определите коэффициент трения нити по блоку. (Ответ: μ = 0,22)
Первый российский паровоз братьев Черепановых мог протащить вагонетку с углем массой 3,2 т на расстояние 3,5 км со скоростью 16 км/ч. Сколько времени он был в движении и какая работа совершалась по перемещению вагонетки, если принять коэффициент трения равным 0,1? (Ответ: 11 МДж; 13 мин).
В 1990 г. во Франции рекордсмен передвинул два железнодорожных вагона общей массой 46 200 кг на 1,5 м. Какую силу тяги он развил и какую работу совершил, если принять коэффициент трения равным 0,01?
(Ответ: 13,6 кДж; 4,5кН).
В 1987 г. в Лондоне рекордсмен совершил буксировку самолета «Конкорд» массой 13 т на расстояние 12,19 м. Какова его сила тяги и какая работа была совершена, если коэффициент трения принять равным 0,02?
(Ответ: 2 кН; 31,1кДж)
В 1988 г. в США один бультерьер передвигал груз массой 2578,5 кг в течение 20,05 с, а второй — 1404 кг в течение 1,64с. Какая из собак развивала большую мощность и во сколько раз? (Ответ: вторая; больше в 6,4 раза).
В 1978 г. в США собака передвинула груз массой 2905 кг на 4,57 м, а спустя 10 дней — груз массой 2993 кг на 4,5 м за это же время. Когда была развита большая мощность?
Один из самых скоростных серийных автомобилей имел мощность 494 л. с. и развивал скорость 325 км/ч при коэффициенте сопротивления 0,31. Каковы его масса и сила тяги (1 л. с. = 735 Вт)? (Ответ: 1319 кг; 4 кН)
Самый тяжелый серийный автомобиль имеет массу 3335 кг и при мощности 315 л. с. способен развить скорость 200 км/ч. Каков коэффициент трения и сила тяги автомобиля?
(Ответ: 0,13; 4,2 кН).
Самая крупная операция по подъему воды из цельного стального бурильного комплекса была осуществлена в 1987 г. в связи с опусканием дна Северного Ледовитого океана. Какая работа была совершена, если масса комплекса 400000 т, а глубина погружения составляла 6,5 м?
Крупнейший в мире 13000-тонный роторный ковшовый экскаватор смонтирован на открытой разработке бурого угля в Гамбахе, ФРГ. Его производительность 200000 м 3 угля за 20-часовой рабочий день, Сколько угля достанет ковш за 20 рабочих дней? (Ответ: 4800000 м 3 )
В Японии построен 240-метровый небоскреб «Саншайн-60» со скоростными пассажирскими лифтами, поднимающими пассажиров до 60-го этажа. Лифты работают со скоростью 36,56 км/ч. Какой кинетической энергией обладают лифты при подъеме? Как изменяется потенциальная энергия пассажира массой 100 кг?
Летающий лыжник Андреас Голлдбергер (Австрия) совершил рекордный прыжок с трамплина на 204 м, 9 марта 1996 года, на соревнованиях на Кубок мира в Харачове, Чехия. Как изменилась потенциальная энергия лыжника, если его масса 80кг? (Ответ: на 163,2 кДж)

На концах рычага действуют силы 2 Н и 18 Н. Длина рычага 1м. Где находятся точка опоры, если рычаг в равновесии?
Балка массой 1200 кг и длиной 3 м лежит на опорах, равноудаленных от ее концов. Расстояние между опорами 2 м. Какую силу, перпендикулярную балке и направленную вертикально вверх, нужно приложить, чтобы приподнять балку за один из её краев? (Ответ: 4,8 кН )
При помощи подвижного блока поднимают груз, прилагая силу 100 Н. Определите силу трения, если вес блока равен 20Н, а вес груза 165 Н. (Ответ: 7,5Н)
Стержень, на одном конце которого подвешен груз весом 120 Н, находится в равновесии в горизонтальном положении, если его подпереть на расстоянии 1/5 длины стержня от груза. Чему равен вес стержня? (Ответ: 80 Н)
Пользуясь системой подвижных и неподвижных блоков, необходимо поднять груз весом 600 Н. Из скольких подвижных блоков должна состоять система, чтобы этот груз мог поднять один человек, прикладывая силу в 65 Н?
(Ответ: 2,3 кН; 92 Н)
На коротком плече рычага подвешен груз массой 100 кг. Для его подъема к длинному плечу приложили силу 250 Н. Груз подняли на высоту 8 см, при этом точка приложения движущейся силы опустилась на высоту 40 см. Найти КПД рычага. (Ответ: 80 %)
При помощи подвижного блока равномерно поднимают груз, прилагая к концу веревки силу 100 Н. Определите силу трения, если масса самого блока равна 2 кг, а масса груза 16,5 кг. Какова будет полезная и затраченная работа и КПД установки, если высота подъема груза 4 м?
ТЕМА 7: АРХИМЕДОВА СИЛА. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
1. Плавание однородного тела в однородной жидкости.
№ 7.1.1: Какую силу надо приложить к пробковому кубу с ребром 0,5 м, чтобы удержать его под водой? ρ = 240 кг/м 3 .
Необходимо приложить силу, равную весу тела в жидкости: Рв воде= Р — Fа,
Где Р – вес тела в воздухе;
Р= mg=ρтgVт=ρтg а 3 =240 кг/м 3 * 10 м/с 2 · (0,5 м) 3 =300Н.
Fа= ρжgVт= 1000 кг/м 3 · 10 м/с 2 · (0,5 м) 3 = 1,25 ·10 3 Н.
Рв воде= 1250 Н – 300 Н= 950 Н.
7.1.2: Кусок металла в воздухе весит 7,8 Н, а в воде – 6,8 Н, в жидкости А — 7 Н, а в жидкости В – 7,1 Н. Определите плотность жидкостей А и В.
Fа= Р — Рв воде= 7,8 Н- 6,8Н= 1 Н. (Сила Архимеда, действующая на кусок металла со стороны воды).
Fа= ρж··gVт; Отсюда находим объём куска металла: 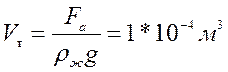
Fа1= Р – Р Ав воде= 7,8 Н — 7Н= 0,8 Н. (Сила Архимеда, действующая на кусок металла со стороны жидкости А).
Fа1= ρжАgVт; Отсюда находим плотность жидкости А: 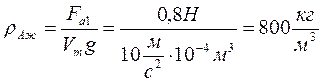
Fа2= Р – РВ в воде= 7,8 Н — 7,1 Н= 0,7 Н. (Сила Архимеда, действующая на кусок металла со стороны жидкости В).
Fа2=ρжВ·gVт; Отсюда находим плотность жидкости В: 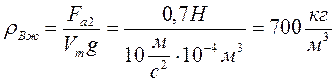
Ответ: 800кг/м 3 ; 7000 кг/м 3 .
7.1.3: Медный шарик в воздухе весит 5,34 Н, а в пресной воде 4,34 Н. Определить объём полости внутри шарика.
Fа=Р — Рв воде= 5,34 Н- 4,34Н= 1 Н. (Сила Архимеда, действующая на медный шарик со стороны воды).
Fа=ρжgVт; Отсюда находим объём медного шарика и полости: 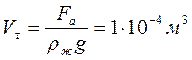
Р=mg – вес медного шарика в воздухе;
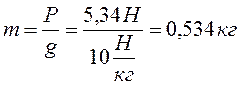
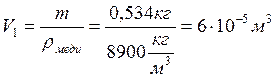
Vполости= V — V1 =10·10 -5 м 3 — 6·10 -5 м 3 =4·10 -5 м 3 .
Ответ: 4·10 -5 м 3 .
7.1.4: Сплошное однородное тело, будучи погружено в жидкость плотностью ρ1, весит Р1, а в жидкости плотностью ρ2 весит Р2. Определите плотность вещества тела.
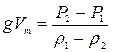
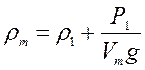
Уравнение (3) подставляем в (4) и получаем: 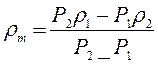
Ответ:
7.1.5: Льдина плавает в воде. Объём её надводной части 20 м 3 . Каков объём подводной части?
Запишем условие плавания тел:
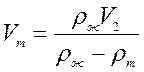
Найдем объём подводной части: 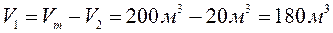
7.1.6: Кусок льда объёмом 5 дм 3 плавает на поверхности воды. Определите объём подводной и надводной части
Запишем условие плавания тел:
Ответ: 0,5·10 -3 м 3 , 4,5·10 -3 м 3 .
7.1.7: Вес однородного тела в воде в n раз меньше, чем в воздухе. Чему равна плотность материала тела? Плотность воды ρ.
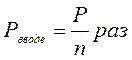
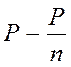
Ответ:
7.1.8: Плотность жидкости в n раз больше плотности материала тела. Какая часть объёма тела будет выступать над поверхностью, если тело поместить в жидкость?
Запишем условие плавания тел:
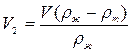
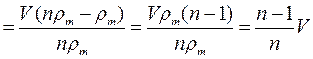
Ответ: V2=
7.1.9: Сосуд объемом V = 1 л заполнен на три четверти водой. Когда в него погрузили кусок меди, уровень воды поднялся и часть ее, объемом V0 = 100 мл, вылилась через край. Найдите массу куска меди. Плотность меди ρ = 8,9 г/см 3 .
Объем Vм куска меди равен объему вытесненной им воды, которая складывается из объема V0 вылившейся воды и объема V1 воды, заполнившей 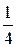
V 1 = 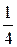
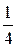
Vм = V0+V1 = 100мл +250мл = 350мл = 350см 3
m = ρ·Vм = 8.9г/см 3 ·350см 3 = 3115 г;
7.1.10: В сосуд объемом V = 1 л, частично заполненный водой, погрузили кусок меди массой m = 3,56 кг, при этом часть воды вылилась через край сосуда. Когда кусок меди вытащили из сосуда, то воды в сосуде осталось 3/4 от исходного объема. Найдите начальный объем воды в сосуде. Плотность меди ρ= 8,9 г/см 3 .
Объем сосуда V складывается из объема Vм куска меди и объема V1 оставшейся в сосуде воды. Пусть V0 — начальный объем воды. Тогда:
Vм = 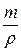
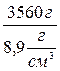
V1 = V — Vм = 1000 см 3 — 400 см 3 =600 см 3
V0 = 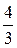
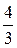
7.1.11: В прямой цилиндрический сосуд, площадь основания которого S=100 см 2 , наливают 1 л соленой воды плотности 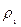
Вначале лед, масса которого m, вытесняет объем воды
V1 = 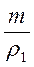
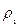
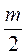
V 2 = 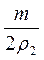
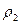
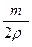
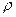
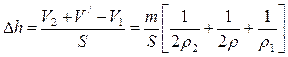
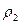
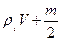
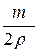
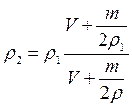
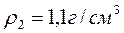
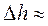
Ответ: таким образом, уровень воды в сосуде повысится.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Деревянный куб с ребром 0,5 м плавает в озере, на 2/3 погруженный в воду. Какую минимальную работу нужно совершить, чтобы утопить куб? (Ответ: 32,5 Дж)
Кусок железа весит в воде 1 H. Определите его объем. Плотность железа 7,8 г/см 3 . (Ответ: 147 см 3 )
Тело в воде весит в три раза меньше, чем в воздухе. Чему равна плотность тела? (Ответ: 1,5 г/см 3 )
Вес однородного тела в воде в n раз меньше, чем в воздухе. Чему равна плотность материала тела? Плотность воды ρ. (Ответ: ρ1= 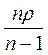
Плотность жидкости в n раз больше плотности материала тела. Какая часть объема тела будет выступать над поверхностью, если тело поместить в жидкость?
(Ответ: V х = 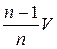

Деревянный шарик плавает на поверхности воды, как показано на рисунке. Определите плотность шарика.

Сосуд объемом V = 1 л заполнен на три четверти водой. Когда в него погрузили кусок меди, уровень воды поднялся и часть ее, объемом V0 = 100 мл, вылилась через край. Найдите массу куска меди. Плотность меди 8,9 г/см 3 . (Ответ: 3115 г.)
Во время экспедиции на дрейфующей льдине в ней пробурили скважину для отбора проб воды. Какую толщину имеет эта льдина, если глубина до поверхности воды в скважине оказалась равной 1,5 м? Плотности льда и воды равны 900 кг/м 3 и 1000 кг/м 3 соответственно. (Ответ: 15 м)
Ко дну цилиндрического стакана с диаметром основания 7 см приморожен ледяной кубик с длиной ребра 4 см. Стакан заливают теплой водой так, что она полностью покрывает кубик. Как и на сколько изменится уровень воды в стакане после того, как кубик полностью растает?
Плотность воды 1,0 г/см 3 , плотность льда 0,9 г/см 3 .
(Ответ: уровень воды опустится на 0,17 см).
2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. ПЛАВАНИЕ НЕОДНОРОДНЫХ ТЕЛ В ОДНОРОДНОЙ ЖИДКОСТИ.
7.2.1. « Вечерело. Уставший за нелегкий день бедный рыбак Абдулла присел на берегу реки отдохнуть. Вдруг видит – плывет по волнам какой – то предмет, почти полностью погруженный в воду, только самый краешек виден на поверхности воды. Абдулла бросился в реку и вытащил его. Смотрит, а это старинный глиняный кувшин, с горлышком, плотно закрытый пробкой и залитый сургучной печатью. Распечатал Абдулла кувшин и обомлел: из кувшина высыпалось 147 одинаковых золотых монет. Монеты Абдулла спрятал, а кувшин закрыл, залил горлышко сургучом и бросил кувшин обратно в реку. И поплыл кувшин дальше, примерно на треть, выступая над водой» — так говорится в одной из восточных сказок.
Полагая, что кувшин был двухлитровым, оцените массу одной золотой монеты.
Сделаем рисунок, покажем все силы, действующие на тело:
Запишем условие плавания тел 1: mg = ρжgVт, отсюда
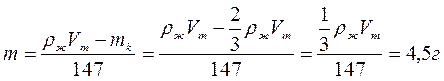
7.2.2: В кастрюле плавает пористый кусок льда. Ровна половина по объёму этого « айсберга» находится над водой. Лёд вынули из воды, при этом её уровень понизился на Δh = 6см. Найдите суммарный объём воздушных полостей в куске льда, если поперечное сечение кастрюли S = 200 см 2 , а плотность льда ρл = 917 кг/м 3 .
Используем закон Архимеда:
Vвыт=SΔh, 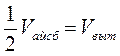
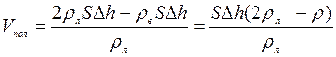
Ответ: 1091 см 3 .
7.2.3: Каков был бы объём короны царя Гиерона, если бы 50% её массы приходилось на серебро, а масса короны составляла бы 4 кг? Каков был бы её объём, если бы она была сделана из чистого золота?
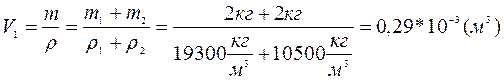
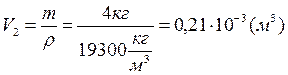
Ответ: 0,29 10 –3 кг/м 3 , 0, 21·10 –3 кг/м 3 .
7.2.4: Предположим, что Архимед взвесил корону царя Гиерона в воздухе и в воде. Определите отношение веса короны в воздухе к её весу в воде для 2 –х случаев, указанных в предыдущей задаче.
1)
2)
Ответ: 1,078 раз; 1,055 раз.
7.2.5: Слиток золота и серебра имеет массу 300 г. При погружении в воду его вес равен 2,75 Н. Определите массу серебра и массу золота в этом слитке.
Р = mg = 0,3 кг·10 Н/кг= 3 Н ( вес тела в воздухе).
Fа= Р — Рв воде= 3 Н- 2,75 Н=0,25 Н (сила Архимеда, действующая на слиток со стороны воды).
Fа=ρжgVт ; Отсюда находим объём тела: 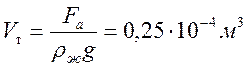
Где объём слитка складывается из объёмов золота и серебра:
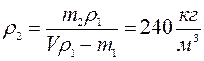
Решая уравнение (1) выразим m2: 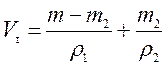
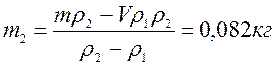
Ответ: 0,082 кг золота; 0,22 кг серебра.
7.2.6: Цинковый шар весит 3,6 Н, а при погружении в воду – 2,8 Н. Сплошной ли этот шар или имеет полость? Если не сплошной, то определите объём полости.
Fа= Р — Рв воде= 3,6 Н- 2,8 Н=0,8 Н (сила Архимеда, действующая на шар со стороны воды).
Fа= ρжgVт; Отсюда находим объём шара ( цинк + полость): 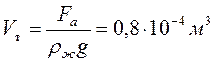
Р = mg ( Вес шарав воздухе). Отсюда 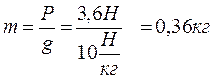
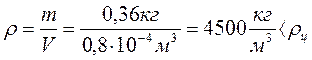
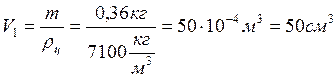
Vпол=V-V1=0,8 10 -4 м 3 – 0,5 10 –4 м 3 = 0,3·10 -4 м 3 =30 см 3 (объём полости).
Ответ: полый; 30см 3 .
7.2.7: Кусок сплава из меди и цинка массой 5,16 кг в воде весит 45,6 Н. Сколько меди содержится в этом сплаве?
Р = mg = 5,16 кг·10 м/с 2 = 51,6 Н ( вес тела в воздухе).
Fа= Р — Рв воде= 51,6 Н- 45,6 Н=6 Н (сила Архимеда, действующая на слиток со стороны воды).
Fа= ρжgVт; Отсюда находим объём тела: 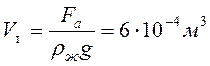
Где объём слитка складывается из объёмов меди и цинка:
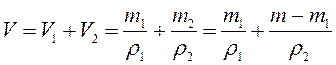
Решая уравнение (1) выразим m1: 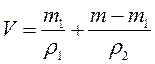
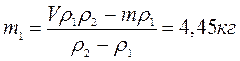
Ответ: 4,45 кг меди.
7.2.8: «Газированный айсберг» представляет собой плоскую ледяную пластинку толщиной Н= 40 см, плотность которой из – за неравномерного распределения пузырьков газа линейно меняется от ρ1= 0,5 до ρ2=0,9 г/см 3 . Найдите высоту надводной части айсберга. Плотность воды ρ = 1 г/см 3 .

 Пусть площадь льдины S, тогда её масса:
Пусть площадь льдины S, тогда её масса:
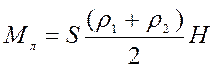

Масса вытесненной воды: 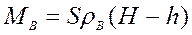
где h – высота надводной части.
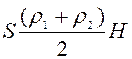
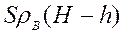
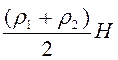
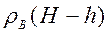
7.2.9: Полый цинковый шар, наружный объём которого 200 см 3 , плавает в воде так, что половина его погружена в воду. Найти объём полости шара Vпол, плотность цинка
Условие плавания тел: mg = ρжgV1, где V1 –объём шара, находящегося в воде.
ρц (V — Vпол) = ρж 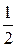
Ответ: 188,9 см 3
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Из чистого ли золота изготовлена царская корона, если её вес в воздухе равен 28,2 Н, а в воде – 26,4 Н? Плотность золота — 19,3 г/см 3 , воды – 1 г/см 3 . (Ответ: нет)
Какая архимедова сила действует на полностью погруженный в воду полый медный шар массой 890 г, если объем полости 40 см 3 . ( Ответ: 1,4 Н)
Цинковый шар весит 3,6 Н, а при погружении в воду – 2,8 Н. Сплошной ли этот шар или имеет полость? Если не сплошной, то определите объем полости. (Ответ: шар имеет полость 30 см 3 ).
Кусок сплава из меди и цинка массой 5,16 кг в воде весит 45,6Н. Сколько меди содержится в этом сплаве? (Ответ: 4,45 кг).
ТЕМА 3: Плавание однородного тела в двух несмешивающихся жидкостях.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
7.3.1. В прямой цилиндрический сосуд, площадь основания которого S = 100 см 2 , наливают 1 л солёной воды плотности ρ1 = 1,15 г/см 3 , и опускают льдинку из пресной воды. Масса льдинки m = 1 кг. Определите, как изменится уровень воды в сосуде, если половина льдинки растает. Считайте, что при растворении соли в воде объём жидкости не изменяется.
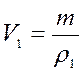
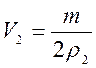
ρ2 – конечная плотность воды.
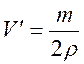
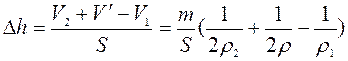
Конечная плотность равна по отношению полной массы воды к полному объему:
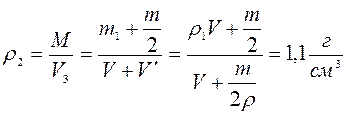
Ответ: т.о. уровень воды в сосуде повысится.
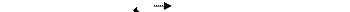
Запишем условие плавания тел: mg=F,
Ответ:
7.3.3: Тело плавает в одной жидкости, погружаясь в неё на 1/4 своего объёма, а в другой жидкости – погружаясь на 2/3 своего объёма. На какую часть объёма погрузится тело в жидкости, плотность которой равна средней арифметической плотностей первых двух жидкостей?
Fа1=ρж1gV1 в первой жидкости. 
Fа2=ρж2gV2 – во второй жидкости. 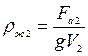
Fа3=ρж3gV3= 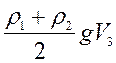
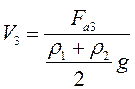
Подставим уравнения (1) и (2) в (3):
Ответ:
7.3.4: Цилиндр, изготовленный из неизвестного материала, плавает на границе двух несмешивающихся между собой жидкостей. Плотность одной жидкости 800 кг/м 3 , а другой – 1000 кг/м 3. Определите плотность вещества цилиндра, если известно, что в нижнюю жидкость он погружен на 2/3 своего объёма.
Запишем условие плавания тел:
Выразим плотность тела:
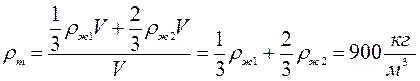
Ответ: 900 кг/м 3
7.3.5: Прямой деревянный цилиндр плавает в воде так, что в неё погружено 0,9 объёма цилиндра. Какая часть цилиндра будет погружена в воду, если на воду налить слой масла, полностью закрывающий цилиндр? Плотность мала 800 кг/м 3 .

1) Из первого условия определим плотность тела:
ρт = 0,9·1000 кг/м 3 =900 кг/м 3
2) Запишем условие плавания для второго случая:
Ответ:
7.3.6: Доска толщиной 5 см плавает в воде, погрузившись на 70 %. Поверх воды разливается слой нефти толщиной 1 см. На сколько будет выступать доска над поверхностью нефти?
7.3.7: В ванну, заполненную водой, опустили кольцо из парафина. Площадь поперечного сечения отверстия кольца S =300 см 2 , а его высота Н=5 см. Какую массу бензина можно влить внутрь кольца так, чтобы он не попал наружу?
Известны: ρВ =1000кг/м 3 – плотность воды; ρп = 900 кг/м 3 – плотность парафина;
ρб =700 кг/м 3 – плотность бензина;
Пусть S – площадь горизонтального сечения парафинового кольца. Вес кольца уравновешивает сила гидростатического давления: mg=pS , где
m = ρпSH, р = ρВSh, а h — глубина погружения кольца. Отсюда
При заполнении внутренней части кольца бензином гидростатическое давление на уровне нижнего края кольца останется постоянным. Поскольку плотность бензина меньше плотности воды, общая высота слоя бензина и воды внутри кольца будет больше высоты h воды снаружи кольца. Так как парафин в бензине тонет, бензин, в конечном счете, станет переливаться через верхний край кольца. Пусть х – максимальная толщина слоя бензина, влитого внутрь кольца, тогда (Н – х ) – толщина слоя воды внутри кольца. Запишем в аналитическом виде равенство гидростатических давлений:
Решая совместно уравнения (1) и (2) получим:
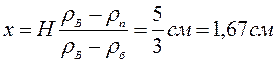
Объём налитого бензина V=Sx =500 см 3 , его масса
7.3.8: Известно, что бензин растекается по поверхности воды, а брусок из липы в бензине не тонет. В ванну, заполненную водой, опустили кольцо из липы. Площадь поперечного сечения отверстия кольца S=300 см 3 , а его высота Н = 5 см. Какую массу бензина можно влить внутрь кольца так, чтобы он не попал наружу? Плотность липы ρл =500 кг/м 3 .
Пусть S – площадь горизонтального сечения липового кольца. Вес кольца уравновешивает сила гидростатического давления: mg=pS , где
m = ρлSH , р = ρВSh, а h— глубина погружения кольца. Отсюда

Решая совместно уравнения (1) и (2) получим:
Поскольку объём бензина внутри кольца V = Sx = 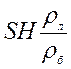
то его масса mб=ρбV= 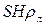
7.3.9: Плавая в первой жидкости, куб погружается на 40 мм, а плавая во второй жидкости – на 60 мм. На сколько миллиметров он погрузится в третьей жидкости, плотность которой равна среднему арифметическому плотностей двух первых жидкостей.
Fа1=ρж1gV1 в первой жидкости. 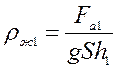
Fа2=ρж2gV2 – во второй жидкости. 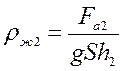
Fа3=ρж3gV3= 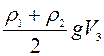
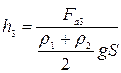
Подставим уравнения (1) и (2) в (3):
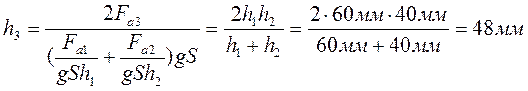
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Кусок металла в воздухе весит 7,8 Н, в воде – 68 Н, в жидкости А — 7 Н, а в жидкости В – 7,1 Н. Определите плотности жидкостей А и В. (Ответ: 0,8 г/см 3 , 0,7 г/см 3 )
Стальной кубик с ребром 10 см плавает в ртути. Поверх ртути наливают воду вровень с верхней гранью кубика. Какова высота слоя воды? (Ответ: 4,6 см).
Тело плотностью ρ плавает на границе раздела двух жидкостей с плотностями ρ1 и ρ2 . Какая часть объема тела погружена в нижнюю жидкость? (Ответ: 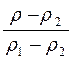
Цилиндр, изготовленный из неизвестного материала, плавает на границе двух несмешивающихся между собой жидкостей. Плотность одной жидкости 800 кг/м 3 , а другой 1000 кг/м 3 . Определите плотность вещества цилиндра, если известно, что в нижнюю жидкость он погружен на 2/3 своего объема. (Ответ: 900 кг/м 3 ).
На границе раздела двух жидкостей плотностей ρ1 и ρ2 плавает шайба плотности ρ (ρ1 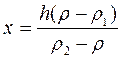
ТЕМА 4: Плавание двух и более тел в однородной жидкости.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
№ 7.4.1. Для участия в Технической олимпиаде по подводному плаванию в Баренцевом море Чебурашка изготовил модель крокодила Гены. Однако модель оказалась слишком тяжелой и тонула в воде. Чебурашка прикрепил к ней несколько герметичных полиэтиленовых пакетов с воздухом. Оказалось, что в Баренцевом море, где плотность воды ρс=1050 кг/м 3 , при погружении на глубину , не превышающуюю критической величины hс= 7 м, модель всплывает, а при погружении на большую глубину тонет. В устье реки Печоры, где плотность воды равна ρп =1000 кг/м 3 , критическая глубина погружения модели крокодила составила всего hп = 1 м. Найдите плотность модели крокодила Гены.
Примечание: Для воздуха применим закон Бойля – Мариотта. Для постоянного количества газа при неизменной температуре произведение давления р газа на занимаемый им объём V постоянно:
Обозначим через: М, ρм, Vм – массу, плотность, объём модели крокодила;
V0, Vс, Vп – объёмы воздуха в полиэтиленовых пакетах соответственно над водой, и при погружении на критическую глубину в морской и речной воде;
р0 – атмосферное давление.
Из условия плавания тел:
Уравнение (1) делим на уравнение (2):
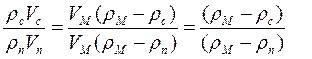
При погружении объём воздуха в полиэтиленовых пакетах уменьшается, причем согласно закону Бойля – Мариотта:
р0V0=(р0+ ρсghс)Vс , 
р0V0=(р0+ ρпghп)Vп , 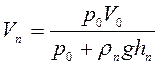
Решая уравнение получим:
Ответ: 1149, 6 кг/м 3 .

Запишем условия плавания кубиков:
где h1 и h2 – глубина погружения первого и второго кубиков. Длина ребер кубиков, выступающих из воды, можно записать в виде:
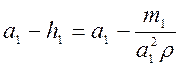
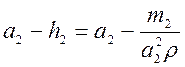
Подстановка чисел приводит к заключению, что
т.е. воду необходимо наливать во второй кубик. Массу воды, которую нужно налить можно вычислить по формуле:
m=ρV= ρa 2 2Δh . , где Δh – разность длин ребер, выступающих из воды. Следовательно,
m=ρa 2 2(а2-h2-а1+h1)=ρa 2 2(а2-а1)-а2 2 ( 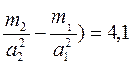
7.4. 3: К куску железа массой 11,7 г привязан кусок пробки массой 1,2 г. При полном погружении этих тел в воду их вес равен 64 мН. Определить плотность пробки.
Вес пробки и куска железа в воздухе:
Fа= Р — Рв воде=12,9·10 -2 Н- 6,4·10 -2 Н= 6,5·10 -2 Н (сила Архимеда, действующая на пробку и кусок железа со стороны воды).
Fа=ρжgVт ; Отсюда находим объём тела: 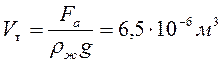
Где объём тела складывается из объёмов куска железа и пробки:
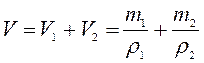
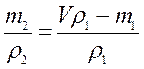
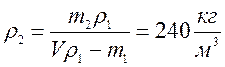
Ответ: 240 кг/м 3.
№ 7.4.4: Деревянная доска плавает в воде таким образом, что под водой находится ¾ её объёма. Какой минимальной величины груз нужно закрепить сверху на доске, чтобы она полностью погрузилась в воду?
1)V1 =3/4 V- объём доски, который находится под водой;
2) запишем условие плавания тел, для доски и груза:
Ответ: 250 кг/м 3
1. А.И. Буздин, А.Р. Зильберман, С.С. Кротов. « Раз задача, два задача…». М.: «Наука», 1990. – 240с.
2. Л.А. Кирик. «Самостоятельные и контрольные работы по физике» 8 класс.. Моква – Харьков. «Илекса», «Гимназия», 1999. – 128 с.
3. М.С. Цедрик. Сборник задач по курсу общей физики. М.: «Просвещение», 1989. – 271 с
4. Н.И. Гольдфарб. Задачник. М.: «Дрофа», 1996. – 368 с.
5. С.М. Козел, В.П. Слободянин. «Всероссийские олимпиады по физике». 1992-2001., М.: «Вербум — М», 2002. – 392с.
Источник











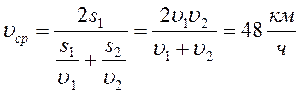
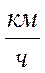
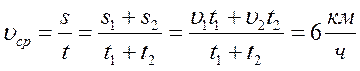
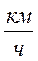
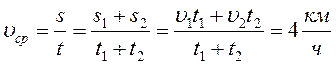
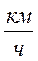
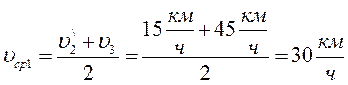
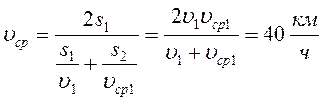
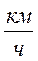
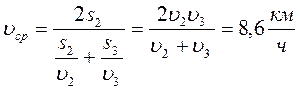
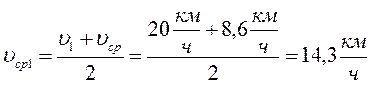
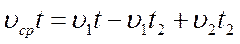
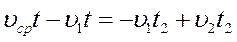
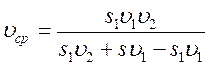
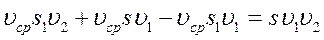
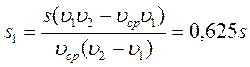
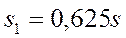
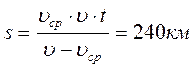
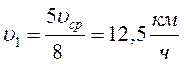
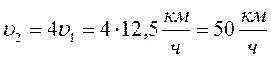
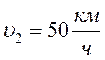
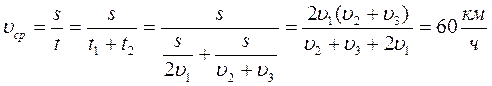
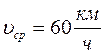
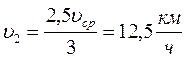
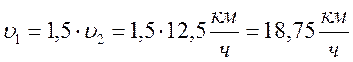
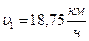
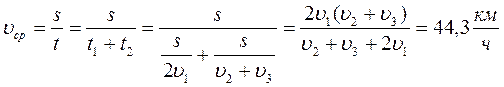
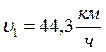
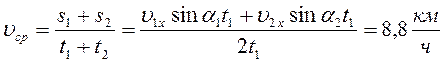
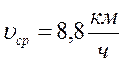
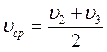
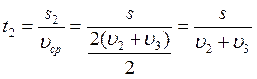
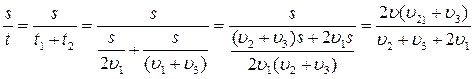
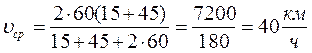

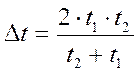
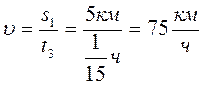
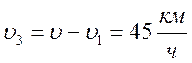
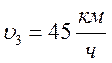
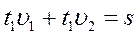
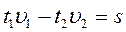
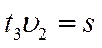
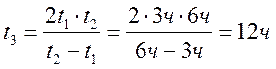
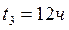
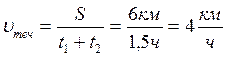
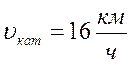
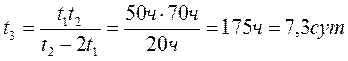
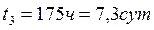
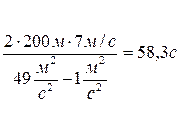

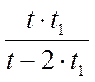
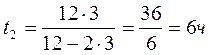

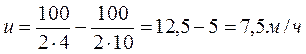
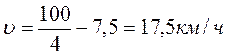
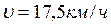
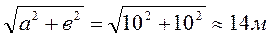
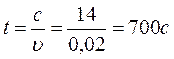
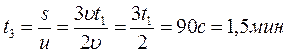
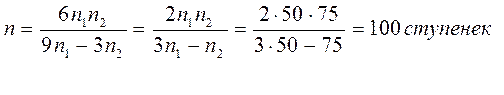
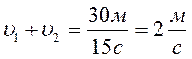
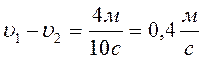
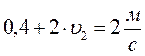
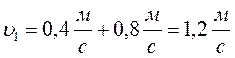
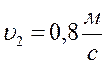
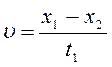
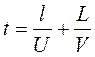
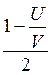
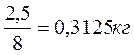
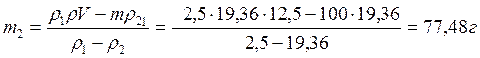
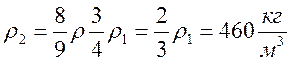
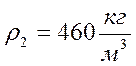
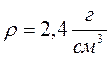
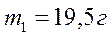
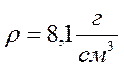


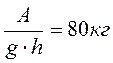
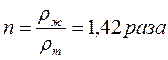
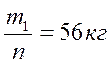
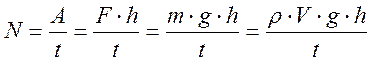
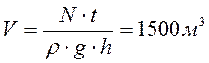
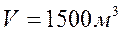
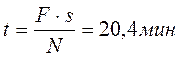
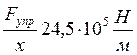
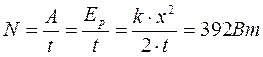
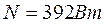
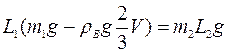
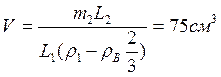

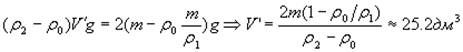

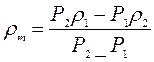
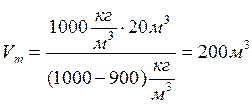
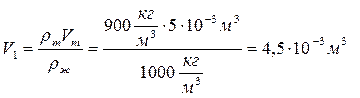
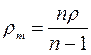
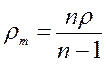
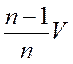
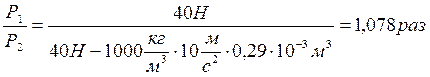
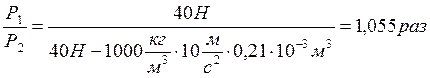
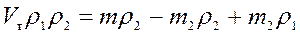
 Пусть площадь льдины S, тогда её масса:
Пусть площадь льдины S, тогда её масса: