Задача про таракана валентина
оБ ЧЩРПМОЕОЙЕ ЪБДБОЙС ЫЛПМШОЙЛБН ДБЧБМПУШ 2 ЮБУБ (120 НЙОХФ).
ъБДБЮБ 1. [3 ВБММБ] фБТБЛБО чБМЕОФЙО ПВЯСЧЙМ, ЮФП ХНЕЕФ ВЕЗБФШ УП УЛПТПУФША 50 Н/НЙО. еНХ ОЕ РПЧЕТЙМЙ, Й РТБЧЙМШОП: ОБ УБНПН ДЕМЕ чБМЕОФЙО ЧУЈ РЕТЕРХФБМ Й ДХНБМ, ЮФП Ч НЕФТЕ 60 УБОФЙНЕФТПЧ, Б Ч НЙОХФЕ 100 УЕЛХОД. у ЛБЛПК УЛПТПУФША (Ч «ОПТНБМШОЩИ» Н/НЙО) ВЕЗБЕФ ФБТБЛБО чБМЕОФЙО?
тЕЫЕОЙЕ. чБМЕОФЙО РТПВЕЗБЕФ 50*60=3000 УН ЪБ 100 У, ФП ЕУФШ ЕЗП УЛПТПУФШ 30 УН/У, ЮФП УПУФБЧМСЕФ 18 Н/НЙО.
ъБДБЮБ 2. [3 ВБММБ]
оБ БЧФПВХУЕ ЕЪДЙМ бОДТЕК
оБ ЛТХЦПЛ Й ПВТБФОП ДПНПК,
ъБРМБФЙЧ 115 ТХВМЕК,
рПЛХРБМ ПО УЕВЕ РТПЕЪДОПК.
ч СОЧБТЕ ПО ЕЗП ОЕ ДПУФБМ,
й РПЬФПНХ ОЕУЛПМШЛП ДОЕК
х ЫПЖЈТБ ВЙМЕФ РПЛХРБМ
пО УЕВЕ ЪБ 15 ТХВМЕК.
б Ч ЙОПК ДЕОШ ЛПОДХЛФПТ У ОЕЗП
вТБМ 11 ФПМШЛП ТХВМЕК.
чПЪЧТБЭБСУШ У ЛТХЦЛБ УЧПЕЗП
чУСЛЙК ТБЪ ЫЈМ РЕЫЛПН ОБЫ бОДТЕК.
ъБ СОЧБТШ УЛПМШЛП ДЕОЕЗ ХЫМП,
рПУЮЙФБМ ВЕТЕЦМЙЧЩК бОДТЕК:
у ХДЙЧМЕОЙЕН ПО РПМХЮЙМ
бЛЛХТБФ 115 ТХВМЕК!
уПУЮЙФБКФЕ ФЕРЕТШ РПУЛПТЕК,
уЛПМШЛП ТБЪ ВЩМ ЛТХЦПЛ Ч СОЧБТЕ?
тЕЫЕОЙЕ. лПМЙЮЕУФЧП ТХВМЕК, РПФТБЮЕООЩИ бОДТЕЕН Ч ФЕ ДОЙ, ЛПЗДБ ПО РПЛХРБМ ВЙМЕФ Х ЫПЖЈТБ, ДЕМЙФУС ОБ 5; ОБ 5 ДЕМЙФУС Й ПВЭЕЕ ЛПМЙЮЕУФЧП РПФТБЮЕООЩИ ЙН Ч СОЧБТЕ ТХВМЕК. ъОБЮЙФ, Й Ч ДТХЗЙЕ ДОЙ ПВЭЕЕ ЛПМЙЮЕУФЧП РПФТБЮЕООЩИ ДЕОЕЗ ДЕМЙМПУШ ОБ 5. рПЬФПНХ, ЛПМЙЮЕУФЧП ДОЕК, ЛПЗДБ бОДТЕК РПЛХРБМ ВЙМЕФ Х ЛПОДХЛФПТБ, ДЕМЙФУС ОБ 5. юЙУМБ 0 Й 10 ОЕ ЗПДСФУС; ЮЙУМБ, ВПМШЫЙЕ 10 — ФЕН ВПМЕЕ, РПЬФПНХ ЕДЙОУФЧЕООЩК ЧПЪ- НПЦОЩК ЧБТЙБОФ — 5 ДОЕК. фПЗДБ ПУФБМШОЩИ ДОЕК (115-11*5)/15=4, Б ЛТХЦПЛ ВЩМ 9 ТБЪ.
ъБДБЮБ 3. мЙУБ Й ДЧБ НЕДЧЕЦПОЛБ ДЕМСФ 100 ЛПОЖЕФ. мЙУБ ТБУЛМБДЩЧБЕФ ЛПОЖЕФЩ ОБ ФТЙ ЛХЮЛЙ; ЛПНХ ЛБЛБС ДПУФБОЕФУС — ПРТЕДЕМСЕФ ЦТЕВЙК. мЙУБ ЪОБЕФ, ЮФП ЕУМЙ НЕДЧЕЦБФБН ДПУФБОЕФУС ТБЪОПЕ ЛПМЙЮЕУФЧП ЛПОЖЕФ, ФП ПОЙ РПРТПУСФ ЕЈ ХТБЧОСФШ ЙИ ЛХЮЛЙ, Й ФПЗДБ ПОБ ЪБВЕТЈФ ЙЪМЙЫЕЛ УЕВЕ. рПУМЕ ЬФПЗП ЧУЕ ЕДСФ ДПУФБЧЫЙЕУС ЙН ЛПОЖЕФЩ.
Б) [2 ВБММБ] рТЙДХНБКФЕ, ЛБЛ мЙУЕ ТБЪМПЦЙФШ ЛПОЖЕФЩ РП ЛХЮЛБН ФБЛ, ЮФПВЩ УЯЕУФШ ТПЧОП 80 ЛПОЖЕФ (ОЙ ВПМШЫЕ, ОЙ НЕОШЫЕ).
В) [4 ВБММБ] нПЦЕФ МЙ мЙУБ УДЕМБФШ ФБЛ, ЮФПВЩ Ч ЙФПЗЕ УЯЕУФШ ТПЧОП 65 ЛПОЖЕФ?
пФЧЕФ. Б) 10, 10 Й 80; В) ОЕФ.
тЕЫЕОЙЕ. Б) мЙУБ ТБУЛМБДЩЧБЕФ ЛПОЖЕФЩ ФБЛ: 10, 10 Й 80. еУМЙ ЕК ДПУФБОЕФУС ЛХЮЛБ ЙЪ 80 ЛПОЖЕФ, ФП НЕДЧЕЦБФБН ДПУФБОЕФУС РПТПЧОХ ЛПОЖЕФ, Й ПОЙ ОЕ ВХДХФ ЦБМПЧБФШУС. еУМЙ ЕК ДПУФБОЕФУС ЛХЮЛБ ЙЪ 10 ЛПОЖЕФ, ФП, ДМС ФПЗП ЮФПВЩ ХТБЧОСФШ ДПМЙ НЕДЧЕЦБФ, ЕК РТЙДЈФУС УЯЕУФШ ЕЭЈ 70 ЛПОЖЕФ.
рТЙНЕЮБОЙЕ. нПЦОП РПЛБЪБФШ, ЮФП ЬФП — ЕДЙОУФЧЕООЩК УРПУПВ ДЕКУФЧЙС мЙУЩ. ч УБНПН ДЕМЕ, РПУЛПМШЛХ Ч ЙФПЗЕ МЙУБ УЯЕУФ 80 ЛПОЖЕФ, ФП НЕДЧЕЦБФБ УЯЕДСФ РП (100-80)/2=10 ЛПОЖЕФ. фБЛ ЛБЛ Х ПДОПЗП ЙЪ НЕДЧЕЦБФ ЛПМЙЮЕУФЧП ЛПОЖЕФ ОЕ НЕОСМПУШ, ФП Ч ЛХЮЛЕ, ДПУФБЧЫЕКУС ЕНХ РП ЦТЕВЙА, ВЩМП 10 ЛПОЖЕФ. уМЕДПЧБФЕМШОП, ЛБЛБС ВЩ ЛХЮЛБ ОЙ ДПУФБМБУШ мЙУЕ РП ЦТЕВЙА, УТЕДЙ ДЧХИ ПУФБЧЫЙИУС ПВСЪБФЕМШОП ЕУФШ ЛХЮЛБ ЙЪ 10 ЛПОЖЕФ. фП ЕУФШ ЛХЮЕЛ РП 10 ЛПОЖЕФ РП ЛТБКОЕК НЕТЕ ДЧЕ (ЕУМЙ ВЩ ФБЛБС ЛХЮЛБ ЙЪ 10 ЛПОЖЕФ ВЩМБ МЙЫШ ПДОБ, ФП ПОБ РП ЦТЕВЙА НПЗМБ ДПУФБФШУС мЙУЕ, Й УТЕДЙ ДЧХИ ПУФБЧЫЙИУС ОЕ ОБЫМПУШ ВЩ ЛХЮЛЙ ЙЪ 10 ЛПОЖЕФ). уМЕДПЧБФЕМШОП, мЙУБ НПЦЕФ ТБЪМПЦЙФШ ЛПОЖЕФЩ РП ЛХЮЛБН ФБЛ, ЮФПВЩ Ч ЙФПЗЕ РПМХЮЙФШ ТПЧОП 80 ЛПОЖЕФ, ЕДЙОУФЧЕООЩН УРПУПВПН.
В) рПЛБЦЕН, ЮФП ЮЙУМП ЛПОЖЕФ, УЯЕДЕООЩИ мЙУПК, ЧУЕЗДБ ЮЈФОП (Й РПЬФПНХ ОЕ НПЦЕФ ВЩФШ ТБЧОЩН 65). ч ЙФПЗЕ НЕДЧЕЦБФБ УЯЕМЙ РПТПЧОХ ЛПОЖЕФ, РПЬФПНХ УХННБТОПЕ ЮЙУМП ЛПОЖЕФ, УЯЕДЕООЩИ НЕДЧЕЦБФБНЙ, ЮЈФОП. фБЛ ЛБЛ 100 — ЮЈФОПЕ ЮЙУМП, ФП мЙУБ ФБЛЦЕ УЯЕМБ ЮЈФОПЕ ЮЙУМП ЛПОЖЕФ.
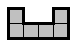
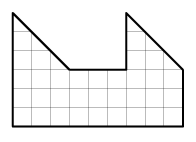
ъБДБЮБ 4. оЕЪОБКЛБ ТБЪНЕУФЙМ ВЕЪ ОБМПЦЕОЙК Ч ЛЧБДТБФЕ 10*10 ФПМШЛП 13 ЖЙЗХТ («УЛПВПЛ»), ЙЪПВТБЦЈООЩИ ОБ ТЙУХОЛЕ. рПРТПВХКФЕ ТБЪНЕУФЙФШ ВПМШЫЕ.
[ъБ ЛБЦДХА УЛПВЛХ УЧЕТИ ФТЙОБДГБФЙ — 2 ВБММБ ]
пФЧЕФ. нПЦОП ТБЪНЕУФЙФШ 14, 15 ЙМЙ ДБЦЕ 16 «УЛПВПЛ». вПМШЫЕ ТБЪНЕУФЙФШ ОЕМШЪС, ФБЛ ЛБЛ 17 «УЛПВПЛ» ЪБОЙНБАФ ХЦЕ 102 ЛМЕФЛЙ.

ъБДБЮБ 5. [6 ВБММПЧ] ч ЮЙУМБИ нйибкмп Й мпнпопупч ЛБЦДБС ВХЛЧБ ПВПЪОБЮБЕФ ГЙЖТХ (ТБЪОЩН ВХЛЧБН УППФЧЕФУФЧХАФ ТБЪОЩЕ ГЙЖТЩ). йЪЧЕУФОП, ЮФП Х ЬФЙИ ЮЙУЕМ РТПЙЪЧЕДЕОЙС ГЙЖТ ТБЧОЩ. нПЗХФ МЙ ПВБ ЮЙУМБ ВЩФШ ОЕЮЈФОЩНЙ?
тЕЫЕОЙЕ. ъБНЕФЙН, ЮФП ЙУРПМШЪПЧБОЩ 10 ТБЪМЙЮОЩИ ВХЛЧ, РПЬФПНХ ЛБЦДБС ГЙЖТБ ПВПЪОБЮЕОБ ЛБЛПК-ОЙВХДШ ВХЛЧПК, Ч ЮБУФОПУФЙ, УТЕДЙ ЬФЙИ ГЙЖТ ЕУФШ ОХМШ. фБЛЙН ПВТБЪПН, РТПЙЪЧЕДЕОЙЕ ГЙЖТ ПДОПЗП (Б ЪОБЮЙФ, Й ЧФПТПЗП) ЮЙУМБ ТБЧОП ОХМА. уМЕДПЧБФЕМШОП, Ч ЪБРЙУЙ ПВПЙИ ЮЙУЕМ ЕУФШ ОХМШ. ч УМПЧБИ нйибкмп Й мпнпопупч ПВЭЙЕ ВХЛЧЩ н, м Й п, РПЬФПНХ ОХМШ ПВПЪОБЮБЕФ ПДОБ ЙЪ ОЙИ. ьФП ОЕ НПЗХФ ВЩФШ м Й н, РПУЛПМШЛХ ЮЙУМБ ОЕ НПЗХФ ОБЮЙОБФШУС У ОХМС. ъОБЮЙФ, ОХМШ ПВПЪОБЮЕО ВХЛЧПК п. ч ЮЙУМЕ нйибкмп ОБ ЛПОГЕ ОХМШ, ФП ЕУФШ ПОП ЮЈФОПЕ.
ъБДБЮБ 6. ч рХУФПЪЕНШЕ ЦЙЧХФ ФТЙ РМЕНЕОЙ: ЬМШЖЩ, ЗПВМЙОЩ Й ИПВВЙФЩ. ьМШЖ ЧУЕЗДБ ЗПЧПТЙФ ФПМШЛП РТБЧДХ, ЗПВМЙО ЧУЕЗДБ МЦЈФ, Б ИПВВЙФ ЮЕТЕЪ ТБЪ ЗПЧПТЙФ ФП РТБЧДХ, ФП МПЦШ. пДОБЦДЩ ЪБ ЛТХЗМЩН УФПМПН РЙТПЧБМП ОЕУЛПМШЛП РХУФПЪЕНГЕЧ, Й ПДЙО ЙЪ ОЙИ УЛБЪБМ, ХЛБЪБЧ ОБ УЧПЕЗП МЕЧПЗП УПУЕДБ: «пО — ИПВВЙФ». уПУЕД УЛБЪБМ: «нПК РТБЧЩК УПУЕД УПМЗБМ». ч ФПЮОПУФЙ ФХ ЦЕ ЖТБЪХ ЪБФЕН РПЧФПТЙМ ЕЗП МЕЧЩК УПУЕД, РПФПН ЕЈ ЦЕ РТПЙЪОЈУ УМЕДХАЭЙК РП ЛТХЗХ, Й ФБЛ ПОЙ ЗПЧПТЙМЙ «нПК РТБЧЩК УПУЕД УПМЗБМ» НОПЗП-НОПЗП ЛТХЗПЧ, ДБ Й УЕКЮБУ ЕЭЈ, ЧПЪНПЦОП, ЗПЧПТСФ.
пРТЕДЕМЙФЕ, ЙЪ ЛБЛЙИ РМЕНЈО ВЩМЙ РЙТХАЭЙЕ, ЕУМЙ ЙЪЧЕУФОП, ЮФП ЪБ УФПМПН УЙДЕМП
Б) [4 ВБММБ] ДЕЧСФШ;
В) [4 ВБММБ] ДЕУСФШ
ЦЙФЕМЕК рХУФПЪЕНШС. пВЯСУОЙФЕ УЧПЈ ТЕЫЕОЙЕ.
пФЧЕФ. Б) чУЕ ВЩМЙ ИПВВЙФБНЙ; В) РСФШ ЗПВМЙОПЧ Й РСФШ ЬМШЖПЧ.
тЕЫЕОЙЕ. тБУУНПФТЙН ФПЗП, РТП ЛПЗП УЛБЪБМЙ, ЮФП ПО — ИПВВЙФ, Й ДМС ХДПВУФЧБ ОБЪПЧЈН ЕЗП вПВ. вПВ ОЕ УПЗМБУЙМУС У ФЕН, ЮФП ПО ИПВВЙФ, УМЕДХАЭЙК ОЕ УПЗМБУЙМУС У ОЙН, Б ЪОБЮЙФ, РПДФЧЕТДЙМ, ЮФП вПВ ИПВВЙФ, Й ФБЛ ДБМЕЕ — ЧУЕ ЗПЧПТСЭЙЕ ЮЕТЕЪ ТБЪ РПДФЧЕТЦДБМЙ ЙМЙ ПФТЙГБМЙ, ЮФП вПВ ИПВВЙФ. еУМЙ РЙТХАЭЙИ ВЩМП 9 (ОЕЮЈФОПЕ ЮЙУМП), ФП ОБ УМЕДХАЭЕН ЛТХЗЕ ЛБЦДЩК ЗПЧПТЙМ РТПФЙЧПРПМПЦОПЕ Л ФПНХ, ЮФП УЛБЪБМ ОБ РТЕДЩДХЭЕН, ФБЛ ЮФП ЧУЕ ПОЙ ИПВВЙФЩ, Б РЕТЧЩК ИПВВЙФ РТП вПВБ УЛБЪБМ УОБЮБМБ РТБЧДХ, ЮФП ЧРПМОЕ ЧПЪНПЦОП. нЩ ТЕЫЙМЙ РХОЛФ Б) ЪБДБЮЙ. дМС ТЕЫЕОЙС РХОЛФБ В) ЪБНЕФЙН, ЮФП, РПУЛПМШЛХ 10 — ЮЈФОПЕ ЮЙУМП, ФП ЗПЧПТСЭЙЕ ОБ ЛБЦДПН ЛТХЗЕ ЗПЧПТСФ ПДОП Й ФП ЦЕ, РПЬФПНХ ИПВВЙФПЧ УТЕДЙ ОЙИ ОЕФ. фПЗДБ Й вПВ — ОЕ ИПВВЙФ, Б УЛБЪБЧЫЙК ФБЛ РТП ОЕЗП ЕЗП РТБЧЩК УПУЕД УПМЗБМ, ФП ЕУФШ ПО ЗПВМЙО. уБН ЦЕ вПВ ХМЙЮЙМ ЗПВМЙОБ ЧП МЦЙ, ФБЛ ЮФП ПО ЬМШЖ. еЗП УПУЕД УМЕЧБ УОПЧБ ЗПВМЙО, Й ФБЛ ДБМЕЕ — ЪБ УФПМПН УЙДСФ, ЮЕТЕДХСУШ, РСФШ ЗПВМЙОПЧ Й РСФШ ЬМШЖПЧ.
Источник
Решение олимпиадных задач
Задачи школьного этапа олимпиады должны быть такой сложности, чтобы не отпугнуть учащихся, а дать им возможность продемонстрировать свои лучшие качества.
Скачать:
| Вложение | Размер |
|---|---|
| reshenie_olimpiadnyh_zadach.pptx | 97.6 КБ |
Предварительный просмотр:
Подписи к слайдам:
Решения олимпиадных задач Предмет математики настолько серьезен, что нельзя упускать случая, сделать его немного занимательным. Блез Паскаль.
Цель олимпиады по математике — способствовать поиску наиболее одаренных школьников . Важной особенностью задач, используемых при проведении школьного и муниципального этапов, является ориентация их на проверку развития у учащихся теоретического мышления, логики, а также творческих способностей и интуиции. Задачи школьного этапа олимпиады должны быть такой сложности, чтобы не отпугнуть учащихся, а дать им возможность продемонстрировать свои лучшие качества.
Основные критерии отбора олимпиадных задач для проведения школьного и муниципального этапов Всероссийской олимпиады школьников по информатике оригинальная формулировка задачи (или идея ее решения); в тексте условия задачи не должны встречаться термины и понятия, выходящие за пределы изучаемых в рамках базового учебного плана предметов; задача должна быть однозначно определена; задача не должна требовать для своего решения специальных знаний; формулировка задачи должна предполагать наличие этапа формализации при ее решении; задача должна быть разумной сложности и трудоемкости.
Основные типы и методы решения олимпиадных задач В ходе изучения научной литературы нами были выявлены следующие типы олимпиадных задач для учащихся 5-7 класса: Числовые ребусы; Арифметика Задачи на взвешивание, переливания; Логические задачи; Задачи на движение или работу; Задачи на раскраску или разрезание; Задачи содержащие идеи четности или делимости; Задачи на проценты и отношения Задачи, решаемые с конца Геометрические задачи;
Задача 1. Можно ли из цифр 1, 2, 3, 4, 5 составить одно двузначное и одно трехзначное число так, чтобы второе делилось на первое? Каждая цифра должна быть использована ровно один раз. Решение: Можно. 532 делится на 14, а 215 делится на 43.
Задача 2. Когда за доброе дело правитель страны решил наградить умного человека, тот пожелал взять столько золота, сколько весит слон. Но как же взвесить слона? В те времена не было таких весов. Что бы в подобной ситуации смогли придумать вы? Решение: Мудрец сделал так: он поместил слона в лодку, затем отметил по борту уровень воды. Когда слона вывели из лодки, осталось только поместить туда золото.
Задача 3. Таракан Валентин объявил, что умеет бегать со скоростью 50 м/мин. Ему не поверили, и правильно: на самом деле Валентин всё перепутал и думал, что в метре 60 сантиметров, а в минуте 100 секунд. С какой скоростью (в «нормальных» м/мин) бегает таракан Валентин? Решение: Валентин пробегает 50*60=3000 см за 100 с, то есть его скорость 30 см/с, что составляет 18 м/мин.
Задача 4 В каждой клетке квадрата 9 × 9 сидит жук. По команде каждый жук перелетает на одну из соседних по диагонали клеток. Доказать, что по крайней мере 9 клеток после этого окажутся свободными. Решение: Раскрасим доску в четыре цвета, так чтобы каждый цвет образовывал раскраску «в горошек». Назовём цвет, в который окрашены угловые клетки, синим, а цвет, в который окрашены клетки, примыкающие к угловым по диагонали – красным. На синие клетки жуки могут перелетать только с красных. Остаётся заметить, что синих клеток на 9 больше, чем красных. Стоит заметить, что мы здесь имеем дело с той же самой шахматной раскраской, но применённой к диагоналям.
Задача 5 Докажите , что произведение любых трех последовательных чисел делится на 6. Решение . Среди трех последовательных чисел есть как минимум одно четное и одно, делящееся на 3. Значит, их произведение разделится на 6.
Задача 6 Женя за весну похудел на 20 %, потом поправился за лето на 30 %, за осень опять похудел на 20 % и за зиму прибавил в весе 10 %. Остался ли за этот год его вес прежним ? Решение: Если Женя весил x кг, то после уменьшения веса на 20 % он стал весить 0,8x кг, а после увеличения веса на 30 % – 0,8x·1,3 кг и т. д., в итоге Женя весил 0,8x·1,3·0,8·1,1 или 0,9152x кг , что меньше x кг. Значит, Женя похудел.
Задача 7 Группа туристов отправилась в поход. В первый день они прошли 1/3 пути, в второй – 1/3 остатка, в третий – 1/3 нового остатка. В результате им осталось пройти 32 км. Сколько километров был маршрут туристов? Решение: Так как осталось 32 км, а в третий день туристы прошли остаток, то 32 км будут составлять последнего 2/3 остатка, тогда сам последний остаток будет равен 32 : 2/3 = 48 (км). Эти 48 км будут составлять 2/3 длины маршрута, оставшегося пройти после первого дня. Тогда весь маршрут, который осталось пройти, будет равен 48 : 2/3 = 72 (км). Эти 72 км составляют вновь 2/3, но уже всего маршрута туристов, а значит, весь маршрут будет равен 72 : 2/3 = 108 (км).
Задача 8 Нарисовать треугольник, который можно разделить на 5 равных треугольников. Решение. Очевидно , что треугольник можно разделить на 4 равные части. Далее к этому треугольнику требуется «приставить» его четвертую часть; при этом снова должен получиться треугольник. Это возможно только в том случае, когда треугольник является прямоугольным, ведь только тогда сумма двух прямых углов даст развернутый угол (отрезок, который является стороной треугольника, при этом будет суммой сторон большого треугольника и его «четвертушки»). Покажем на рисунке решение задачи. Необходимо нарисовать прямоугольный треугольник, у которого один катет в два раза длиннее
Задача 9 Задачи на переливания, которые решаются с помощью алгебраического метода. Задача: Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал? Решение: Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л. Решение лучше и удобнее оформить в виде таблицы: Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг ). Шаг Сосуд – 3л Сосуд – 5л 1 0 5 2 3 2 3 0 2 4 2 0 5 2 5 6 3 4
Методы решения задач по математике Доказательство от обратного (противного ). Метод математической индукции . Принцип Дирихле . Метод Кругов Эйлера Метод раскраски..
Памятка участнику олимпиады. Прочитайте все задачи и наметьте, в каком порядке вы будете их решать. Помните последние задачи обычно более сложные. Если для вас задача решалась слишком легко, то, скорее всего вы не поняли условие или где-то ошиблись. Если задача не решается – попробуйте упростить ее условие (взять меньшие числа, рассмотреть частные случаи и т.д ) или порешать ее «с конца», «от противного», поставить вместо чисел переменные и т.д. Не зацикливайтесь на одной задаче: иногда отрывайтесь от нее и оценивайте положение. Если есть хоть небольшие успехи, то можно продолжать, а если мысль ходит по кругу, то задачу лучше оставить, хотя бы на время. Почувствовав усталость – отдохните (посмотрите в окно, закройте глаза, отвлекитесь). Решив задачу, сразу оформите ее решение. Это поможет проверить рассуждения и освободить мысли для других задач. Перед сдачей работы, проверьте еще раз написанное – поймут ли ваши решения задач члены жури?
Источник
13 задач Матпраздника: выбор главного редактора
| Алексей Горбачев 13 февраля 2017 |